Курс. Структура программы. Основные математические операции и типы данных
 Скачать 492.5 Kb. Скачать 492.5 Kb.
|
данном учебном пособии рассматривается внутренний язык программирования MatLab, дающий наибольшую гибкость, богатство функционала и удобство при решении и исследовании математических задач. При изложении материала предпочтение отдавалось наиболее простым конструкциям языка, изучая которые можно создавать самые разнообразные и нетривиальные математические алгоритмы. Данная программа заключена в функции с именем Lab1 и вычисляет произведение двух переменных а и b. При сохранении программы в m-файл рекомендуется указывать имя файла, совпадающее с именем функции, т.е. в данном случае – Lab1.
2-й файл (square.m)    function res=square(a, b) res = a*b;  При выполнении функции Lab1 система MatLab вызовет функцию square из файла square.m. Это будет сделано автоматически, т.к. встроенные функции языка MatLab определены также и вызываются из файлов, имена которых, как правило, соответствуют именам вызываемых функций. Обратите также внимание на то, что функция square() не только принимает два аргумента a и b, но и возвращает их произведение с помощью переменной res. Представленный синтаксис следует использовать всякий раз, когда требуется возвратить результат вычислений основной программе. В четвертой главе данного пособия более подробно изложены конструкции вызова функций для реализации разнообразных алгоритмов. 1.2. Простые переменные и основные типы данных в MatLab Создание программы, как правило, начинается с определения переменных и способа представления данных. Следовательно, чтобы правильно организовать описание данных программы, необходимо знать как задавать переменные в MatLab и какие виды переменных возможны. Самый простой и наиболее распространенный тип данных – это число. В MatLab число хранится в переменной, которая имеет некоторое уникальное имя, например, a = 5; задает переменную с именем a и присваивает ей значение 5. По умолчанию переменная а является вещественной (тип double), т.е. может принимать дробные значения, например, a = -7.8; задает значение переменной а равное -7,8. Изменить тип переменной можно, указав тип присваиваемого числа с помощью соответствующего ключевого слова, например, a = int16(5) выполнит присваивание числа 5 как целочисленного 16-битового значения. В результате выполнения такой операции тип переменной a будет соответствовать int16. Типы данных, доступные в MatLab, представлены в табл. 1.1. Таблица 1.1 – Основные типы данных в MatLab
По умолчанию используется тип double, который имеет наибольшую точность представления вещественного числа и является потому универсальным типом. Однако, если необходимо экономить память ЭВМ, то можно указывать самостоятельно желаемый тип. Последнее, что следует знать при задании переменных – это правило определения их имен. В MatLab имена переменных могут задаваться только латинскими буквами, цифрами и символом ‘_’. Причем, первый символ в имени должен соответствовать букве латинского алфавита. Также следует отметить, что имена arg = 1; Arg = 2; ARG = 3; это три разных имени, т.е. три разные переменные со значениями 1, 2 и 3 соответственно. Данный пример показывает, что MatLab различает регистр в именах переменных. При программировании лучше всего задавать осмысленные имена переменных, по которым можно было бы понять какие данные они представляют. Это позволяет избежать путаницы при построении больших программ. 1.3. Основные математические функции MatLab MatLab содержит в себе все распространенные математические функции, которые доступны по их имени при реализации алгоритмов. Например, функция sqrt() позволяет вычислять квадрат числа и может быть использована в программе следующим образом: x = 2; y = 4; d = sqrt(x^2+y^2); %вычисление евклидового расстояния Аналогичным образом вызываются и все другие математические функции, представленные в табл. 1.2 Таблица 1.2.- Основные математические функции MatLab.
1.4. Структуры в MatLab При разработке программ важным является выбор эффективного способа представления данных. Во многих случаях недостаточно объявить простую переменную или массив, а нужна более гибкая форма представления данных. Таким элементом может быть структура, которая позволяет включать в себя разные типы данных и даже другие структуры. Структуры задаются следующим образом: S = struct('field1',VALUES1,'field2',VALUES2,...); где field1 – название первого поля структуры; VALUES1 – переменная первого поля структуры, и т.д. Приведем пример, в котором использование структуры позволяет эффективно представить данные. Таким примером будет инвентарный перечень книг, в котором для каждой книги необходимо указывать ее наименование, автора и год издания. Причем количество книг может быть разным, но будем полгать, что не более 100. Для хранения информации об одной книге будем использовать структуру, которая задается в MatLab с помощью ключевого слова struct следующим образом: S = struct('title','','author','','year',0); В итоге задается структура с тремя полями: title, author и year. Каждое поле имеет свой тип данных и значение. Для того, чтобы записать в эту структуру конкретные значения используется оператор ‘.’ (точка) для доступа к тому или иному полю структуры: S.title = 'Евгений Онегин'; S.author = 'Пушкин'; S.year = 2000; и таким образом, переменная S хранит информацию о выбранной книге. Глава 2. Условные операторы и циклы в MatLab Вторым шагом создания полноценных программ на языке MatLab является изучение операторов ветвления и циклов. С их помощью можно реализовывать логику выполнения математических алгоритмов и создавать повторяющиеся (итерационные, рекуррентные) вычисления. 2.1. Условный оператор if Для того чтобы иметь возможность реализовать логику в программе используются условные операторы. Умозрительно эти операторы можно представить в виде узловых пунктов, достигая которых программа делает выбор по какому из возможных направлений двигаться дальше. Например, требуется определить, содержит ли некоторая переменная arg положительное или отрицательное число и вывести соответствующее сообщение на экран. Для этого можно воспользоваться оператором if (если), который и выполняет подобные проверки. В самом простом случае синтаксис данного оператора if имеет вид: if <выражение> <операторы> end Если значение параметра «выражение» соответствует значению «истинно», то выполняется оператор, иначе он пропускается программой. Следует отметить, что «выражение» является условным выражением, в котором выполняется проверка некоторого условия. В табл. 2.1 представлены варианты простых логических выражений оператора if. Таблица 2.1. Простые логические выражения
2.2. Условный оператор switch
switch expr case case_expr, <операторы1> case {case_expr1, case_expr2, case_expr3,...} <операторы2> ... otherwise, <операторы> end Здесь expr – переменная, значение которой проверяется на равенство тем или иным константам; case_expr – константы, с которым сравнивается значение переменной; otherwise – ключевое слово, для выполнения операторов, при всех ложных условиях. 2.3. Оператор цикла while Язык программирования MatLab имеет два оператора цикла: while и for. С их помощью, например, выполняется программирование рекуррентных алгоритмов, подсчета суммы ряда, перебора элементов массива и многое другое. В самом простом случае цикл в программе организуется с помощью оператора while, который имеет следующий синтаксис: while <условие> <операторы> end Здесь <условие> означает условное выражение подобное тому, которое применяется в операторе if, и цикл while работает до тех пор, пока это условие истинно. Следует обратить внимание на то, что если условие будет ложным до начала выполнения цикла, то операторы, входящие в цикл, не будут выполнены ни разу. 2.4. Оператор цикла for Часто при организации цикла требуется перебирать значение счетчика в заданном диапазоне значений и с заданным шагом изменения. Например, чтобы перебрать элементы вектора (массива), нужно организовать счетчик от 1 до N с шагом 1, где N – число элементов вектора. Чтобы вычислить сумму ряда, также задается счетчик от a до b с требуемым шагом изменения step. И так далее. В связи с тем, что подобные задачи часто встречаются
Синтаксис оператора цикла for имеет следующий вид: for <счетчик> = <начальное значение>:<шаг>:<конечное значение> <операторы цикла> end Рассмотрим работу данного цикла на примере реализации алгоритма поиска максимального значения элемента в векторе: function search_max a = [3 6 5 3 6 9 5 3 1 0]; m = a(1); % текущее максимальное значение for i=1:length(a) % цикл от 1 до конца вектора с % шагом 1 (по умолчанию) if m < a(i) % если a(i) > m, m = a(i); % то m = a(i) end end % конец цикла for disp(m);
Глава 3. Работа с графиками в MatLab MatLab предоставляет богатый инструментарий по визуализации данных. Используя внутренний язык, можно выводить двумерные и трехмерные графики в декартовых и полярных координатах, выполнять отображение изображений с разной глубиной цвета и разными цветовыми картами, создавать простую анимацию результатов моделирования в процессе вычислений и многое другое. 3.1. Функция plot Рассмотрение возможностей MatLab по визуализации данных начнем с двумерных графиков, которые обычно строятся с помощью функции plot(). Множество вариантов работы данной функции лучше всего рассмотреть на конкретных примерах. Предположим, что требуется вывести график функции синуса в диапазоне от 0 до x = 0:0.01:pi;
y = sin(x); и выведем результат на экран plot(x,y); В результате получим график, представленный на рис. 3.1. Представленная запись функции plot() показывает, что сначала записывается аргумент со множеством точек оси Ох, а затем, аргумент со множеством точек оси Oy. Зная эти значения, функция plot() имеет возможность построить точки на плоскости и линейно их интерполировать для придания непрерывного вида графика. 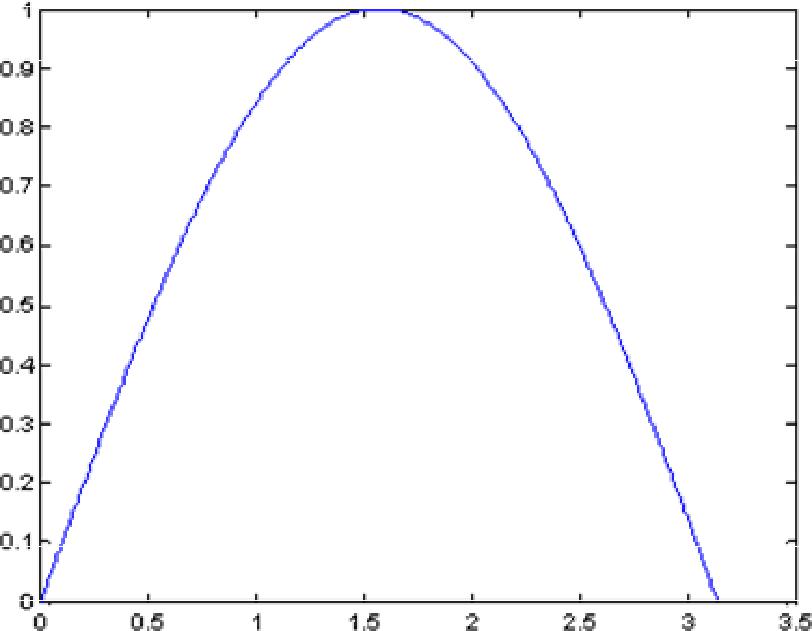 Рис. 3.1.- Отображение функции синуса с помощью функции plot(). Функцию plot() можно записать и с одним аргументом x или y: plot(x); plot(y); в результате получим два разных графика, представленные на рис. 3.2. Анализ рис. 3.2 показывает, что в случае одного аргумента функция plot() отображает множество точек по оси Oy, а по оси Оx происходит автоматическая генерация множества точек с единичным шагом. Следовательно, для простой визуализации вектора в виде двумерного графика достаточно воспользоваться функцией plot() с одним аргументом. Для построения нескольких графиков в одних и тех же координатных осях, функция plot() записывается следующим образом: x = 0:0.01:pi; y1 = sin(x); y2 = cos(x); plot(x,y1,x,y2); Результат работы данного фрагмента программы представлен на рис. 3.3. 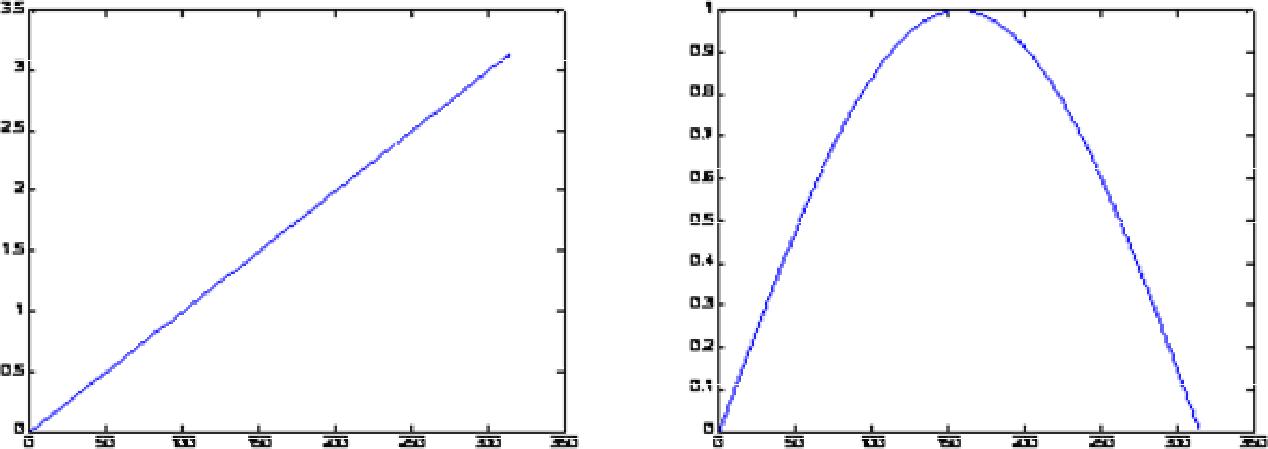 а) б) Рис. 3.2.-Результаты работы функции plot() с одним аргументом: а– plot(x); б – plot(y). 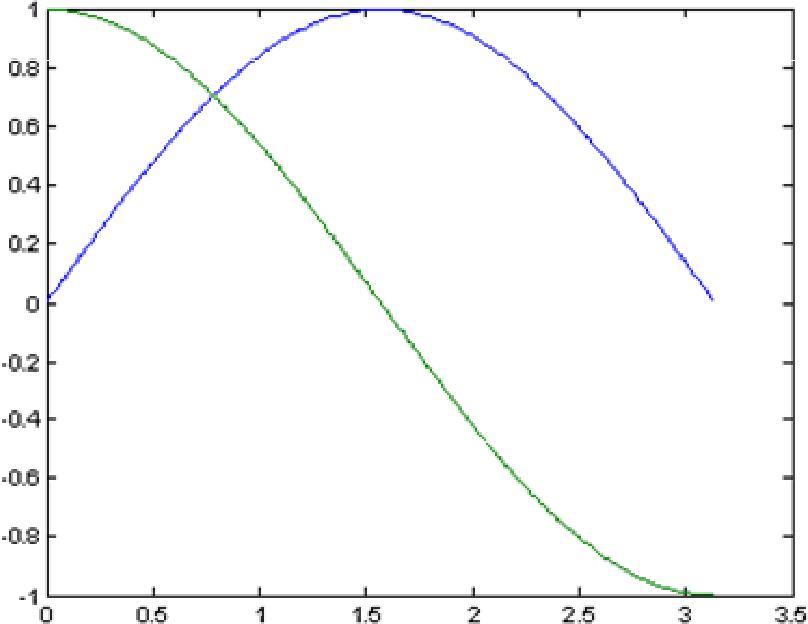 Рис. 3.3.-Отображение двух графиков в одних координатных осях. Аналогичным образом можно построить два графика, используя один аргумент функции plot(). Предположим, что есть два вектора значений y1 = sin(x); y2 = cos(x) которые требуется отобразить на экране. Для этого объединим их в двумерную матрицу 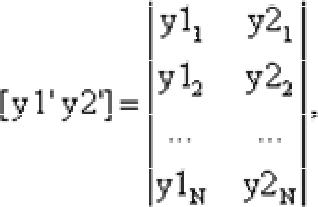 в которой столбцы составлены из векторов y1 и y2 соответственно. Такая матрица будет отображена функцией plot([y1’ y2’]); % апострофы переводят вектор-строку
в виде двух графиков (рис. 3.4). 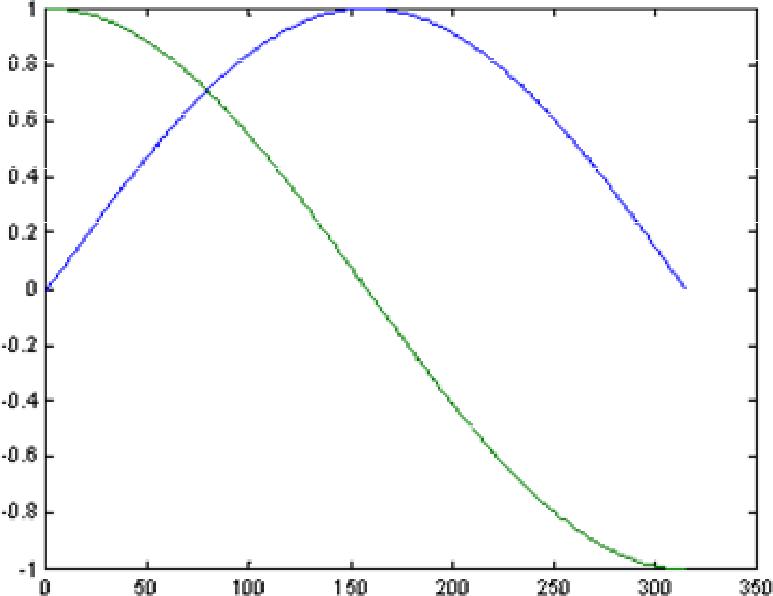 Рис. 3.4.-Отображение двумерной матрицы в виде двух графиков. 4 Практическая часть (с использованием программного комплекса Matlab)Цепи с одним источником энергии целесообразно рассчитывать методом эквивалентного преобразования. При расчете придерживаемся следующей последовательности.
Дано: 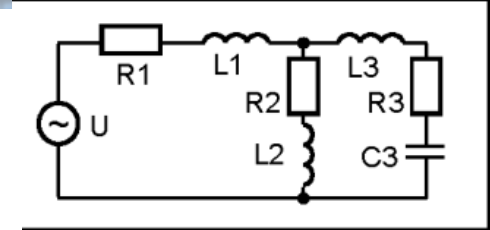 Рисунок 2.1 - Задание
При расчете реактивных сопротивлений индуктивности подставляются в формулы в генри (Гн), а емкости в фарадах (Ф). С1 = 1.0000e-004 L1 = L2 = 0.0159 L3 = 0.1150 

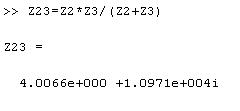 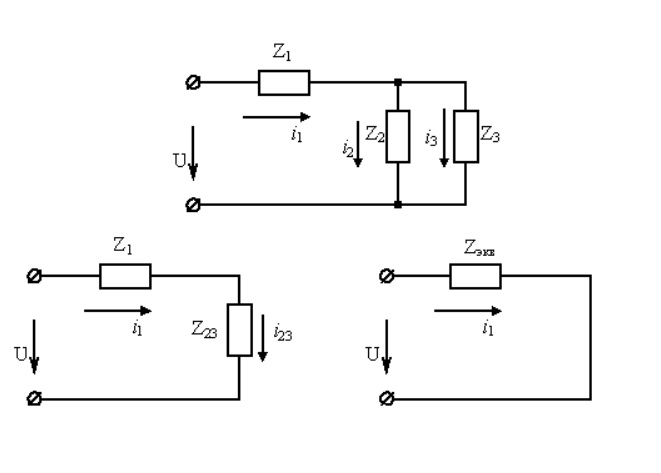 Рисунок 4.1 - Эквивалентные схемы расчетной цепи
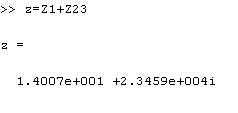

 7. Комплексы токов в параллельных ветвях можно рассчитать, пользуясь законом Ома, т. к. комплексы полных сопротивлений параллельных ветвей известны, а комплекс на параллельном участке определен в предыдущем пункте:  8. Баланс комплексных мощностей В соответствии с законом сохранения энергии, комплекс мощности источника должен быть равен сумме комплексов мощностей всех ветвей цепи:  Для проверки примем S1+S2+S3=X И сравним S и X.  Как видно S и X равны, следовательно, расхождение балансов равно 0%. 9. Построим векторные диаграммы, согласно нашим расчетам 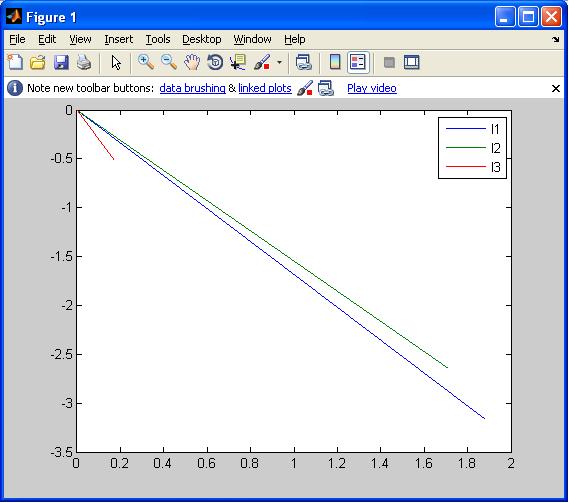 Рисунок 4.2- Векторная диаграмма токов 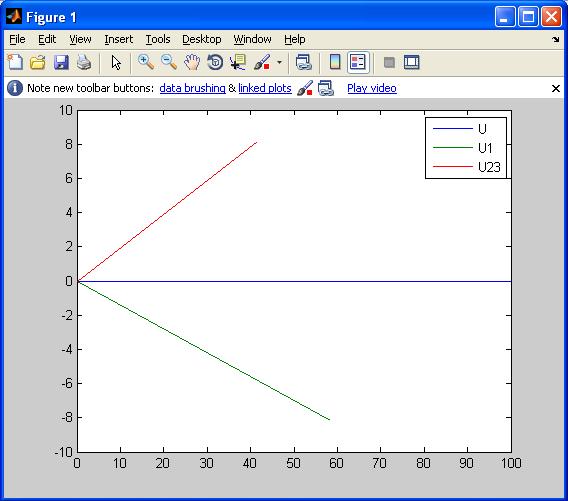 Рисунок 4.3 - Векторная диаграмма напряжений Список литературы
|
