отчёт по лр гидравлика. гидравлика отчёт по лр3. Студент гр. Нтс18 Кириллова О. А
 Скачать 129.88 Kb. Скачать 129.88 Kb.
|
|
ПЕРВОЕ ВЫСШЕЕ ТЕХНИЧЕСКОЕ УЧЕБНОЕ ЗАВЕДЕНИЕ РОССИИ  МИНИСТЕРСТВО науки и высшего ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ федеральное государственное бюджетное образовательное учреждение высшего образования «САНКТ-ПЕТЕРБУРГСКИЙ ГОРНЫЙ УНИВЕРСИТЕТ» Кафедра автоматизации технологических процессов и производств ОТЧЁТ По лабораторным работам Выполнил: студент гр. НТС-18 Кириллова О.А. (подпись) (ФИО) Проверил: доцент Кускова Я.В. (подпись) (ФИО) Санкт-Петербург 2020 г. Цель работы: приобрести навыки экспериментального определения скорости свободного падения зерен, оценить влияние на скорость свободного падения таких разделительных признаков зерен, как плотность, крупность и форма. Основные понятия Свободное падение – падение единичного зерна в неограниченном пространстве среды или падение массы зерен при небольшой объемной концентрации их в сосуде, в котором происходит падение (практический случай) Объемная концентрация (объёмная доля) падающих зерен (падающего твёрдого) – отношение объёма этих зерен к объему сосуда, в котором происходит их падение, выраженное, обычно, в долях единицы: 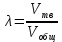 где 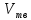 – объём падающих зерен (объём твердого); – объём падающих зерен (объём твердого); 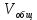 – объём, где происходит падение, или объём взвеси падающих зерен (объём твердого и объём среды). – объём, где происходит падение, или объём взвеси падающих зерен (объём твердого и объём среды).Практически считают падение свободным, когда λ≤0,1. Сила сопротивления среды падающему зерну в воде при его свободном падении определяется только гидродинамическим сопротивлением. Механическим сопротивлением, за счет влияния дна и стенок сосуда, трения и удара зерен друг о друга, можно в этом случае пренебречь. Конечной скоростью свободного падения зерна называют его максимальную постоянную скорость в данной среде. Такая скорость достигается в момент, когда вес тела в среде становится равным силе сопротивления среды (гидродинамическому сопротивлению при падении зерна в воде). Выражение для гидродинамического сопротивления имеет разный вид в зависимости от режима падения зерна, который определяется разделительными признаками зерна. Разделительные признаки – плотность, крупность, форма. Крупность зерен сферической формы характеризуется диаметром шара; крупность зерен неправильной (несферической) формы – характерным размером; например эквивалентным диаметром по объёму dэ или по поверхности dS. Эквивалентный диаметр зерна неправильной формы по объёму: 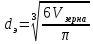 где 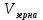 – объём зерна. – объём зерна.Форма зерен характеризуется коэффициентом сферичности χ. Для зерен правильной сферической формы χ = 1, для зерен неправильной формы χ < 1. Конечная скорость падения зерна неправильной формы меньше, чем скорость падения шара (тела) правильной формы. Это уменьшение учитывают с помощью поправочного коэффициента формы, который рассчитывается по экспериментальным данным для конечной скорости свободного падения зерен неправильной формы. Коэффициент формы Кχ - отношение экспериментально определенной конечной скорости свободного падения данного зерна неправильной формы (v0)эксп к теоретической скорости падения, когда реальное зерно заменяют равнообъёмным ему шаром (v0)теор: 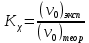 Теоретическую скорость рассчитывают по одной из частных формул для конечной скорости свободного падения. Формулы выбирают с учётом крупности и плотности зерна и параметров среды по значению первого параметра Лященко Re2ψ. В данной работе для расчёта v0 используют формулу Ньютона-Риттингера 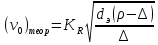 где 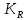 – коэффициент – коэффициент 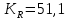 ; ; 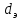 – эквивалентный диаметр зерна, г/см3; – эквивалентный диаметр зерна, г/см3;  - плотность среды, г/см3, для воды - плотность среды, г/см3, для воды  =1 г/см3. =1 г/см3.Скорость падения зерна в неподвижной (спокойной) воде экспериментально определяется как путь, деленный на время, за которое он пройден. Исходные данные:
Таблица измерений:
Пример расчёта для угля: 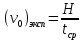 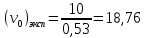 см/с см/с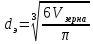 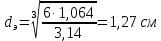 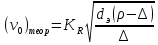 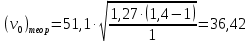 см/с см/с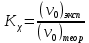 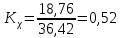 Вывод: в ходе лабораторной работы были приобретены экспериментальные навыки определения скорости свободного падения зерен. Можно сделать вывод, что чем больше плотность и коэффициент сферичности, тем больше скорость свободного падения зерна. №2 Цель работы: приобрести навыки экспериментального определения скорости свободного падения зерен, оценить влияние крупности зерен на скорость свободного падения. Основные понятия Свободное падение – падение единичного зерна в неограниченном пространстве среды или падение массы зерен при небольшой объемной концентрации их в сосуде, в котором происходит падение (практический случай) Объемная концентрация (объёмная доля) падающих зерен (падающего твёрдого) – отношение объёма этих зерен к объему сосуда, в котором происходит их падение, выраженное, обычно, в долях единицы: 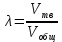 где 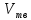 – объём падающих зерен (объём твердого); – объём падающих зерен (объём твердого); 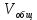 – объём, где происходит падение, или объём взвеси падающих зерен (объём твердого и объём среды). – объём, где происходит падение, или объём взвеси падающих зерен (объём твердого и объём среды).Практически считают падение свободным, когда λ≤0,1. Сила сопротивления среды падающему зерну в воде при его свободном падении определяется только гидродинамическим сопротивлением. Механическим сопротивлением, за счет влияния дна и стенок сосуда, трения и удара зерен друг о друга, можно в этом случае пренебречь. Конечной скоростью свободного падения зерна называют его максимальную постоянную скорость в данной среде. Такая скорость достигается в момент, когда вес тела в среде становится равным силе сопротивления среды (гидродинамическому сопротивлению при падении зерна в воде). Выражение для гидродинамического сопротивления имеет разный вид в зависимости от режима падения зерна, который определяется разделительными признаками зерна. Разделительные признаки – плотность, крупность, форма. Крупность зерен сферической формы характеризуется диаметром шара. Форма зерен характеризуется коэффициентом сферичности χ. Для зерен правильной сферической формы χ = 1, для зерен неправильной формы χ < 1. Конечная скорость падения зерна неправильной формы меньше, чем скорость падения шара (тела) правильной формы. Это уменьшение учитывают с помощью поправочного коэффициента формы, который рассчитывается по экспериментальным данным для конечной скорости свободного падения зерен неправильной формы. Коэффициент формы Кχ - отношение экспериментально определенной конечной скорости свободного падения данного зерна неправильной формы (v0)экспк теоретической скорости падения, когда реальное зерно заменяют равнообъёмным ему шаром (v0)теор: 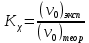 Теоретическую скорость рассчитывают по одной из частных формул для конечной скорости свободного падения. Формулы выбирают с учётом крупности и плотности зерна и параметров среды по значению первого параметра Лященко Re2ψ. В данной работе для расчёта v0 используют формулу Ньютона-Риттингера 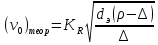 где 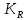 – коэффициент – коэффициент 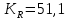 ; ; 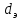 – эквивалентный диаметр зерна, г/см3; – эквивалентный диаметр зерна, г/см3;  - плотность среды, г/см3, для воды - плотность среды, г/см3, для воды  =1 г/см3. =1 г/см3.Скорость падения зерна в неподвижной (спокойной) воде экспериментально определяется как путь, деленный на время, за которое он пройден. Исходные данные:
Таблица измерений:
Пример расчёта: 1. 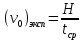 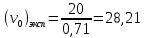 см/с см/с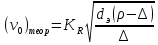 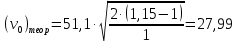 см/с см/с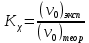 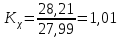 2. 1) 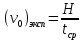 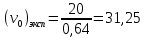 см/с см/с2) 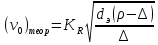 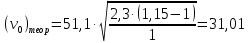 см/с см/с3) 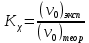 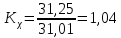 Вывод: в ходе лабораторной работы были приобретены экспериментальные навыки определения скорости свободного падения зерен. Можно сделать вывод, что чем больше крупность зерна, тем больше его скорость свободного падения. №3 С помощью параметра Лященко определим область применения отдельных формул. 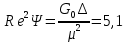 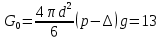 Число Рейнольдса: 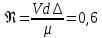 Тела разного размера и разной плотности, имеющие одинаковую конечную скорость падения, называются равнопадающими. Отношение диаметра удельно-легкого шара к диаметру удельно-тяжелого, имеющего ту же конечную скорость падения, называется коэффициентом равнопадаемости. При известной конечной скорости свободного падения можно определить крупность падающего тела, пользуясь вторым параметром Лященко и частными формулами 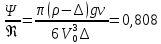 Так как предел применения второго параметра Лященко 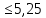 , то размер зерен мелкий и пользуемся формулой коэффициента равнопадаемости. , то размер зерен мелкий и пользуемся формулой коэффициента равнопадаемости.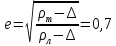 Формула Стокса 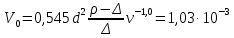 По формуле мы высчитали значение параметра 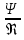 =0,808. =0,808.По найденному значению выбрали частную формулу для конечной скорости свободного падения шара. Теперь по выбранной формуле для конечной скорости свободного падения шара определим для заданного значения требуемую крупность. Формула Ньютона-Ритингера: 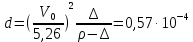 При определении скорости падения минеральных зерен в формуле для расчета необходимо вводить коэффициент формы Р 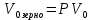 Коэффициент формы определяют опытным путем. Мы рассчитаем его по эмпирическим формулам в зависимости от коэффициента сферичности для мелких зерен: 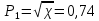 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
