МИНИСТЕРСТВО ОБЩЕГО И ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
СВЕРДЛОВСКОЙ ОБЛАСТИ
ГОСУДАРСТВЕННОЕ АВТОНОМНОЕ ПРОФЕССИОНАЛЬНОЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕСВЕРДЛОВСКОЙ ОБЛАСТИ«НОВОУРАЛЬСКИЙ ТЕХНОЛОГИЧЕСКИЙ КОЛЛЕДЖ»(ГАПОУ СО «НТК»)
КОНТРОЛЬНО-ОЦЕНОЧНЫЕ СРЕДСТВА для проведения промежуточной аттестации
в форме экзамена
по учебной дисциплине ОУД.04«Математика»
ОПОП СПО ППКР(С)
15.01.25 «Станочник (металлообработка)»15.01.30 «Слесарь»15.01.05 «Сварщик (ручной и частично механизированной сварки (наплавки)»23.01.03 «Автомеханик»13.01.10 «Электромонтер по ремонту и обслуживанию электрооборудования (по отраслям)»2017
Организация - разработчик: Государственное автономное профессиональноеобразовательное учреждение Свердловской области «Новоуральский технологический колледж».
Разработчик:Бронских Е.В., преподаватель 1КК;
Шпилько Н.Я., преподаватель 1КК.
Рассмотрена на заседании
научно-методического совета ГАПОУ СО «НТК»
Протокол
№ от «»__________ 20
1 г.
СОДЕРЖАНИЕ
I. Паспорт комплекта оценочных средств 4
|
II. Описание правил оформления результатов оценивания……….5 |
Приложение 1. ЗАДАНИЯ…………………………………………...6
|
Приложение 2. Оценочный лист………………………………… ..37
|
Паспорт комплекта оценочных средств
Данные оценочные средства предназначены для проведения промежуточной аттестации в форме экзамена по учебной дисциплине «Математика» в группахОПОП СПО ППКР(С)
15.01.25 «Станочник (металлообработка)»
15.01.30 «Слесарь»
15.01.05 «Сварщик (ручной и частично механизированной сварки (наплавки)»
23.01.03 «Автомеханик»
13.01.10 «Электромонтер по ремонту и обслуживанию электрооборудования (по отраслям)»
Промежуточная аттестация проходит в конце 4 семестра.
При проведении промежуточной аттестации оцениваются освоенные предметные результаты по математике:
Предметные результаты обучения
|
Показатели результатов обучения
|
сформированность представлений о математике как части мировой культуры и месте математики в современной цивилизации, способах описания явлений реального мира на математическом языке
|
вычисление значения выражения
решение простейшего уравнения/ неравенства
вычисление значения производной функции в заданной точке
вычисление определенного интеграла
решение задачи методом координат
решение задачи по стереометрии
решение задачи по теории вероятностей
решение уравнения
|
сформированность представлений о математических понятиях как о важнейших математических моделях, позволяющих описывать и изучать разные процессы и явления; понимание возможности аксиоматического построения математических теорий
|
владение методами доказательств и алгоритмов решения; умение их применять, проводить доказательные рассуждения в ходе решения задач
|
вычисление значения выражения
решение простейшего уравнения/ неравенства
вычисление значения производной функции в заданной точке
вычисление определенного интеграла
решение задачи методом координат
решение задачи по стереометрии
решение задачи по теории вероятностей
решение уравнения;
преобразование выражения
использование производной функции для нахождения ее промежутков монотонности, точек экстремума, наибольшего и наименьшего значения на отрезке
использование определенного интеграла для вычисления площадей плоских фигур
|
владение стандартными приёмами решения рациональных и иррациональных, показательных, степенных, тригонометрических уравнений и неравенств, их систем; использование готовых компьютерных программ, в том числе для поиска пути решения и иллюстрации решения уравнений и неравенств
|
решение уравнения/ неравенства
|
сформированность представлений об основных понятиях математического анализа и их свойствах, владение умением характеризовать поведение функций, использование полученных знаний для описания и анализа реальных зависимостей
|
вычисление значения производной функции в заданной точке
вычисление определенного интеграла
использование производной функции для нахождения ее промежутков монотонности, точек экстремума, наибольшего и наименьшего значения на отрезке
использование определенного интеграла для вычисления площадей плоских фигур
|
владение основными понятиями о плоских и пространственных геометрических фигурах, их основных свойствах; сформированность умения распознавать геометрические фигуры на чертежах, моделях и в реальном мире; применение изученных свойств геометрических фигур и формул для решения геометрических задач и задач с практическим содержанием
|
решение задачи методом координат
решение задачи по стереометрии
использование определенного интеграла для вычисления площадей плоских фигур
|
сформированность представлений о процессах и явлениях, имеющих вероятностный характер, статистических закономерностях в реальном мире, основных понятиях элементарной теории вероятностей; умений находить и оценивать вероятности наступления событий в простейших практических ситуациях и основные характеристики случайных величин
|
решение задачи по теории вероятностей
|
II. Описание правил оформления результатов оцениванияФормой промежуточной аттестации является экзамен, который проводится письменно.
Экзаменационная работа состоит из двух частей.
Первая часть (задания 1 – 6) включает пять заданий по алгебре и началам анализа и однозадание по геометрии, проверяющих наличие математических знаний и умений базового уровня.
Вторая часть (задания 7 – 9) состоит из двух заданий по алгебре и началам анализа и одного задания по геометрии повышенного уровня сложности.
Задания составлены в соответствии с требованиями к результатам освоения учебной дисциплины.
Работа составлена в 30 вариантах.
Для процедуры аттестации подготовлены задания, разработан оценочный лист, включающий в себя показатели оценки результата и критерии как признаки, которые проявляются/не проявляются в деятельности обучающегося при выполнении экзаменационной работы:
0 баллов – данный признак не проявляется;
1 балл – признак проявляется.
Правильное решение каждого из заданий 1 – 5 оценивается в 2 балла; Правильное решение задания 6 оценивается в 3 балла.
Правильное решение каждого из заданий 7 – 9 оценивается 4 баллами.
Для выполнения экзаменационной работы по учебной дисциплине «Математика» отводится 6 часов (360 минут).
Учебная дисциплина считается освоенной при положительной оценке не менее 51 % критериев. Решение о качестве освоения учебной дисциплины основано на рейтинговой шкале, которая составляет 25 баллов и далее переводится в традиционную 5-тибалльную шкалу:
Процент результативности
|
Количественная оценка индивидуальных образовательных достижений
|
%
|
баллы
|
оценка
|
91-100
|
23-25
|
отлично
|
75-90
|
19-22
|
хорошо
|
52-74
|
13-18
|
удовлетворительно
|
0-51
|
0-11
|
неудовлетворительно
|
Приложение 1ГАПОУ СО НОВОУРАЛЬСКИЙ ТЕХНОЛОГИЧЕСКИЙ КОЛЛЕДЖЭкзаменационный билет № 1 по учебной дисциплине «Математика»
Часть 1
Найти значение выражения  .
.
Решить неравенство  .
.
Найти координаты вектора, если его началом является точка А , а концом точка М
, а концом точка М .
.
На экзамен вынесено 60 вопросов, Андрей не выучил 3 из них. Найти вероятность того, что ему попадется выученный билет.
Упростить выражение 
Вычислить определенный интеграл  .
.
Часть 2
Сторона основания правильной четырехугольной пирамидыSABCDравна 12, высотаSOравна 8. Найти площадь боковой поверхности пирамиды.
Найти корни уравнения  .
.
Найти промежутки возрастания и убывания функции  .
.
|
Преподаватель
|
…………………………………….
|
|
ГАПОУ СО НОВОУРАЛЬСКИЙ ТЕХНОЛОГИЧЕСКИЙ КОЛЛЕДЖЭкзаменационный билет № 2 по учебной дисциплине «Математика»
Часть 1
Найти значение выражения  .
.
Решить уравнение  .
.
Найти длину отрезка ВС, если известно, что В и С
и С .
.
В фирме такси в данный момент свободно 20 машин: 10 черных, 2 желтых и 8 зеленых. По вызову выехала одна из машин, случайно оказавшаяся ближе всего к заказчице. Найдите вероятность того, что к ней приедет зеленое такси.
Упростить выражение 
Вычислить определенный интеграл  .
.
Часть 2
Сторонаоснования правильной четырехугольной пирамидыSABCDравна 8, апофема SOравна 5. Найти объем пирамиды.
Найти корни уравнения  .
.
Найти промежутки возрастания и убывания функции  .
.
|
Преподаватель
|
…………………………………….
|
|
ГАПОУ СО НОВОУРАЛЬСКИЙ ТЕХНОЛОГИЧЕСКИЙ КОЛЛЕДЖЭкзаменационный билет № 3 по учебной дисциплине «Математика»
Часть 1
Найти значение выражения  .
.
Решить неравенство  .
.
В треугольнике АВС А , В
, В , С
, С . Найти координаты точки М, если АМ – медиана треугольника АВС.
. Найти координаты точки М, если АМ – медиана треугольника АВС.
На тарелке 16 пирожков: 7 с рыбой, 5 с вареньем и 4 с вишней. Юля наугад выбирает один пирожок. Найдите вероятность того, что он окажется с вишней.
Упростить выражение  .
.
Вычислить определенный интеграл 
Часть 2
Боковое ребро BS правильной треугольной пирамиды SABC равно 5. Найти площадь боковой поверхности пирамиды, если длина ее апофемы равна 3.
Найти корни уравнения 
Найти промежутки возрастания и убывания функции  .
.
|
Преподаватель
|
…………………………………….
|
|
ГАПОУ СО НОВОУРАЛЬСКИЙ ТЕХНОЛОГИЧЕСКИЙ КОЛЛЕДЖЭкзаменационный билет № 4 по учебной дисциплине «Математика»
Часть 1
Найти значение выражения  .
.
Решить уравнение 
В треугольнике АВС А , В
, В , С
, С . Найти длину стороны АС.
. Найти длину стороны АС.
В случайном эксперименте бросают игральную кость. Найдите вероятность того, что выпадетчисло очков, кратное трем.
Упростить выражение  .
.
Вычислить определенный интеграл  .
.
Часть 2
Боковое ребро BS правильной треугольной пирамиды SABC равно 10. Найти площадь боковой поверхности пирамиды, если сторона ее основания равна12.
Найти корни уравнения  .
.
Найти промежутки возрастания и убывания функции  .
.
|
Преподаватель
|
…………………………………….
|
|
ГАПОУ СО НОВОУРАЛЬСКИЙ ТЕХНОЛОГИЧЕСКИЙ КОЛЛЕДЖЭкзаменационный билет № 5 по учебной дисциплине «Математика»
Часть 1
Найти значение выражения  .
.
Решить неравенство  .
.
Найти расстояние между точками К и Е, если известно, что Е ) а К
) а К .
.
В коробке имеется 10 красных, 15 желтых и 5 синих карандашей. Наудачу вынимают один карандаш. Какова вероятность того, что он синий?
Упростить выражение  .
.
Вычислить определенный интеграл 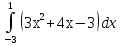 .
.
Часть 2
Длина диагонали А1С прямоугольного параллелепипеда  равна 19. Найти объем параллелепипеда, если СС1 = 6, CD = 17.
равна 19. Найти объем параллелепипеда, если СС1 = 6, CD = 17.
Найти корни уравнения  .
.
Найти наибольшее значение функции  на отрезке
на отрезке  .
.
|
Преподаватель
|
…………………………………….
|
|
ГАПОУ СО НОВОУРАЛЬСКИЙ ТЕХНОЛОГИЧЕСКИЙ КОЛЛЕДЖЭкзаменационный билет № 6 по учебной дисциплине «Математика»
 Скачать 59.07 Kb.
Скачать 59.07 Kb.
 .
. .
. , а концом точка М
, а концом точка М .
.
 .
. .
. .
. .
. .
. и С
и С .
.
 .
. .
. .
. .
. .
. , В
, В , С
, С . Найти координаты точки М, если АМ – медиана треугольника АВС.
. Найти координаты точки М, если АМ – медиана треугольника АВС. .
.

 .
. .
.
 , В
, В , С
, С . Найти длину стороны АС.
. Найти длину стороны АС. .
. .
. .
. .
. .
. .
. ) а К
) а К .
.  .
.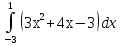 .
. равна 19. Найти объем параллелепипеда, если СС1 = 6, CD = 17.
равна 19. Найти объем параллелепипеда, если СС1 = 6, CD = 17. .
. на отрезке
на отрезке  .
.