Задачи. T, частоту отказов системы f

• Название: T, частоту отказов системы f
• Анкор: Задачи
• Дата: 14.01.2023
• Размер: 39.52 Kb.
• Имя файла: Задачи.docx
• Тип: Закон; #885731

1. 
   Время работы до отказа каждого элемента системы (см. рис.) подчинено экспоненциальному закону распределения с параметром =0,1 1/год. Требуется вычислить количественные характеристики надежности системы: вероятность отказов Q(t), частоту отказов f(t) для t=1 год, среднее время до отказа Тс.
   

2. 
   Время работы до отказа каждого элемента системы (см. рис.) подчинено экспоненциальному закону распределения с параметром =0,1 1/год. Требуется вычислить количественные характеристики надежности системы: безотказность P(t), частоту отказов f(t) для t=1 год, среднее время до отказа Тс.
   

Рис.

3. 
   Время работы до отказа каждого элемента системы (см. рис.) подчинено экспоненциальному закону распределения с параметром =0,1 1/год. Требуется вычислить количественные характеристики надежности системы: вероятность отказов Q(t), частоту отказов f(t) для t=1 год, среднее время до отказа Тс.
   

Рис.

4. 
   В результате анализа данных об отказах аппаратуры частота отказов получена в виде f(t)=0,5∙₁∙e^−1∙t+0,5∙₂∙e^−2∙t. Требуется определить количественные характеристики надежности: безотказность P(t), интенсивность отказов λ(t), среднее время до отказа Тс для t=32∙10⁶ с, ₁= (1/32)∙10^-6 с^-1, ₂= (1/64)∙10^-6 с^-1.
   

5. 
   Для изображенной на рис. логической схемы системы определить вероятность безотказной работы системы P_c(t), частоту отказов системы f_c(t) при t=3 года и среднее время до отказа Тс. Выполняется экспоненциальный закон. Все элементы равнонадежны с параметром =10^-3 год^-1
   

Рис.

6. 
   Схема расчета надежности приведена на рисунке. Необходимо найти вероятность безотказной работы изделия, если известны вероятности отказов элементов.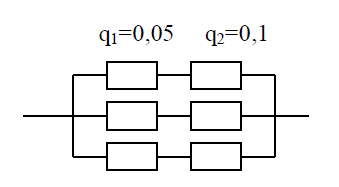