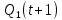Контрольная работа ТДУ. ТДУ контрольная работа. Таблица истинности комбинационного устройства
 Скачать 1.23 Mb. Скачать 1.23 Mb.
|
Требуется синтезировать функциональную логическую схему устройства в базисе И-НЕ, применяя методы минимизации заданной логической функции с помощью алгебраических преобразований и с помощью карт Карно. Если количество наборов значений входных переменных, при которых значение функции равно 1, значительно превышает количество наборов, при которых функция принимает нулевое значение, то применяют совершенную конъюнктивную нормальную форму СДНФ представления ФАЛ, в противном случае, используют совершенную дизъюнктивную нормальную форму СКНФ записи структурной формулы ФАЛ. Минимизация нашей ФАЛ заключается в нахождении нормальной формы ее записи КНФ, имеющей минимальное число вхождений входных переменных. Составим структурную формулу ФАЛ в виде СКНФ: 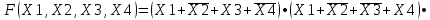  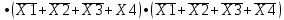 Произведем минимизацию ФАЛ с помощью операции склеивания и поглощения: Аксиома алгебры логики.  : : 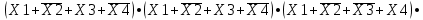 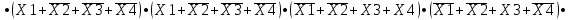 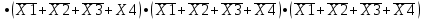 Закон склеивания. 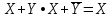 : : 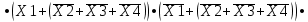 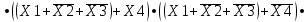   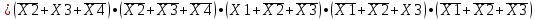 Аксиома алгебры логики.  : :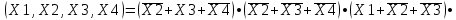 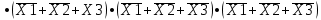 Закон склеивания. 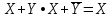 : :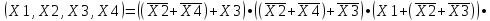 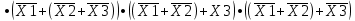 Следовательно:  Составим импликантную таблицу: Метод импликантных таблиц является одним из методов нахождения тупиковых и минимальных КНФ по сокращенным КНФ. В случае если простую импликанту можно получить из конституенты единицы вычеркиванием некоторых букв, то говорят, что импликанта накрывает конституенту. В этом случае клетка импликантной таблицы, соответствующая импликанте и конституенте, отмечается специальным знаком. Минимальной КНФ заданной функции будет соответствовать такая система минимального числа строк таблицы, импликанты которых совместно накрывают крестиками все колонки таблицы.
Получим МКНФ:  Выполним минимизацию с помощью карт Карно: в каждой клетке укажем значение функции, которое она принимает на наборе значений переменных, являющихся ее координатами. Функция представлена в СКНФ, поэтому в каждой клетке, координаты которой соответствуют минтерму, для которого функция принимает единичное значение, укажем значение “0”, а значение “1” при этом на картах отражать не будем. Минимизация ФАЛ заключается в объединении соседних клеток (при этом клетки, лежащие на границах карты, также являются соседними по отношению друг к другу), содержащих нулевые (для получения МКНФ) значения, в замкнутой области. Более удобным методом минимизации является метод, основанный на использовании карт Карно для описания ФАЛ:  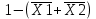   Таким образом, минимальная тупиковая форма:  Для записи, полученной в результате минимизации КНФ, в базисе И-НЕ используем закон де Моргана (закон инверсии), согласно которому дизъюнкция n переменных равна инверсной функции от конъюнкций инверсий этих переменных и, наоборот, конъюнкция n переменных равна инверсной функции от дизъюнкции инверсий этих переменных.   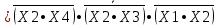 Функциональная схема логического устройства, реализующего функцию 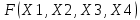 в базисе И-НЕ представлена на рисунке 1. в базисе И-НЕ представлена на рисунке 1.Для реализации ФАЛ используется количество логических элементов типа И-НЕ равное числу инверсий = 5. 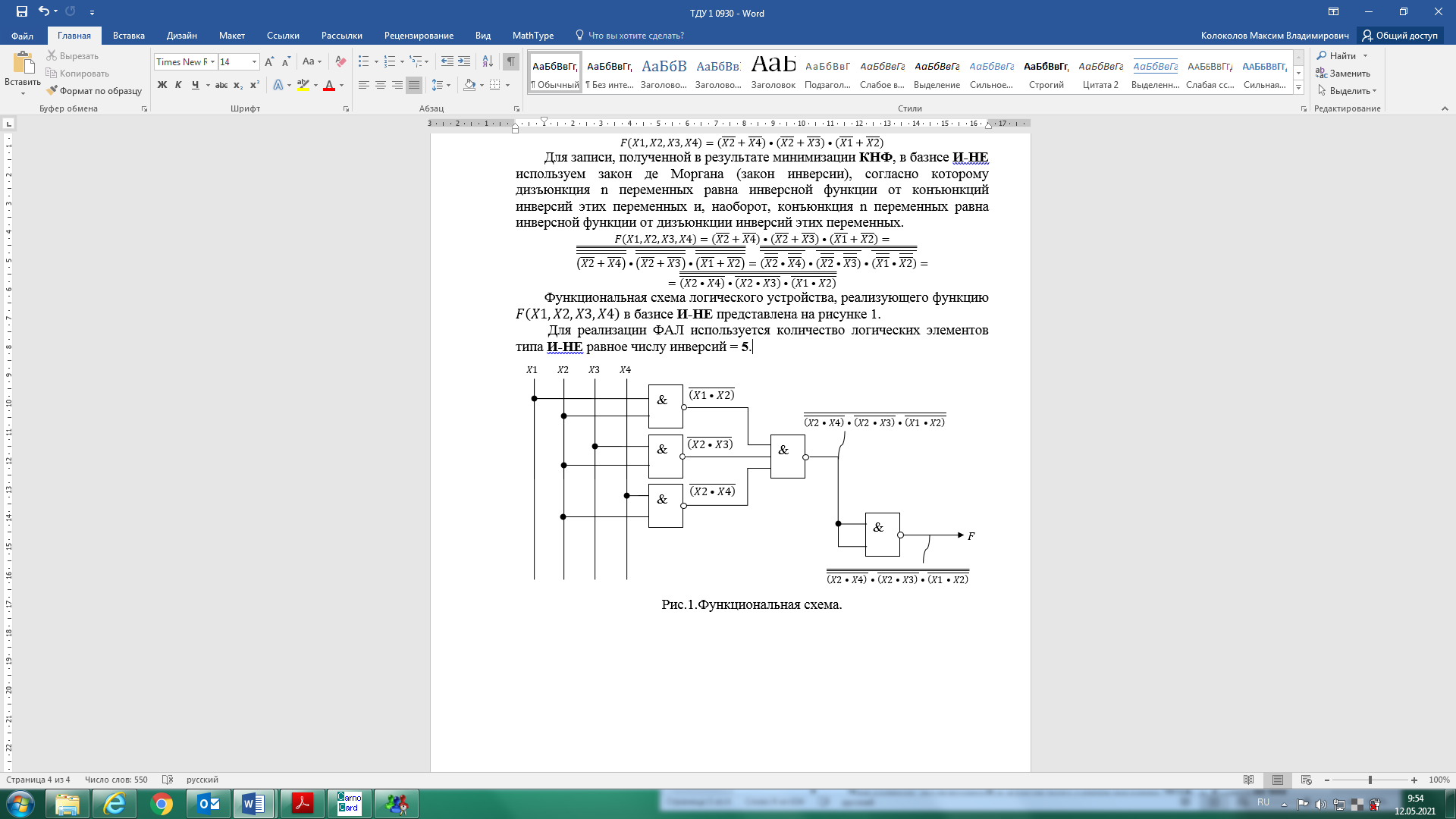 Рис.1.Функциональная схема. Задача 2 Произвести синтез автомата Мили, функционирование которого описывается заданными таблицами переходов и выходов (табл. 2, и 3). Изобразить граф синтезируемого автомата. Построить структурную схему синтезированного автомата в базисе И, ИЛИ, НЕ. Табл.2. Таблица переходов.
Переводим три последние цифры шифра в двоичный код и заносим в таблицу последние восемь разрядов получившегося двоичного числа.  64010 = 1000010010 2 Табл.3. Таблица выходов.
Изобразить граф синтезируемого автомата. Задавая произвольную двоичную последовательность (входное слово), определить соответствующую двоичную выходную последовательность (выходное слово) автомата. Для синтеза комбинационных схем требуется набор логических элементов, реализующих некоторую полную систему логических функций (базис). Особенность последовательностных схем состоит в том, что они обладают памятью, для реализации которой требуются дополнительные элементы. В качестве таких элементов используются триггеры. Автомат Мили является одной из разновидностей последовательностных схем. В автомате Мили выходные сигналы являются функциями его входных сигналов (x1, х2, … , хn) и выходных сигналов триггеров (Q1, Q2, ... , Qm). Функции переходов и выходов автомата могут быть заданы как в форме вышеприведенных таблиц переходов и выходов (табл. 2, и 3), так и с помощью графов. Построим граф состояния для автомата с заданными параметрами: 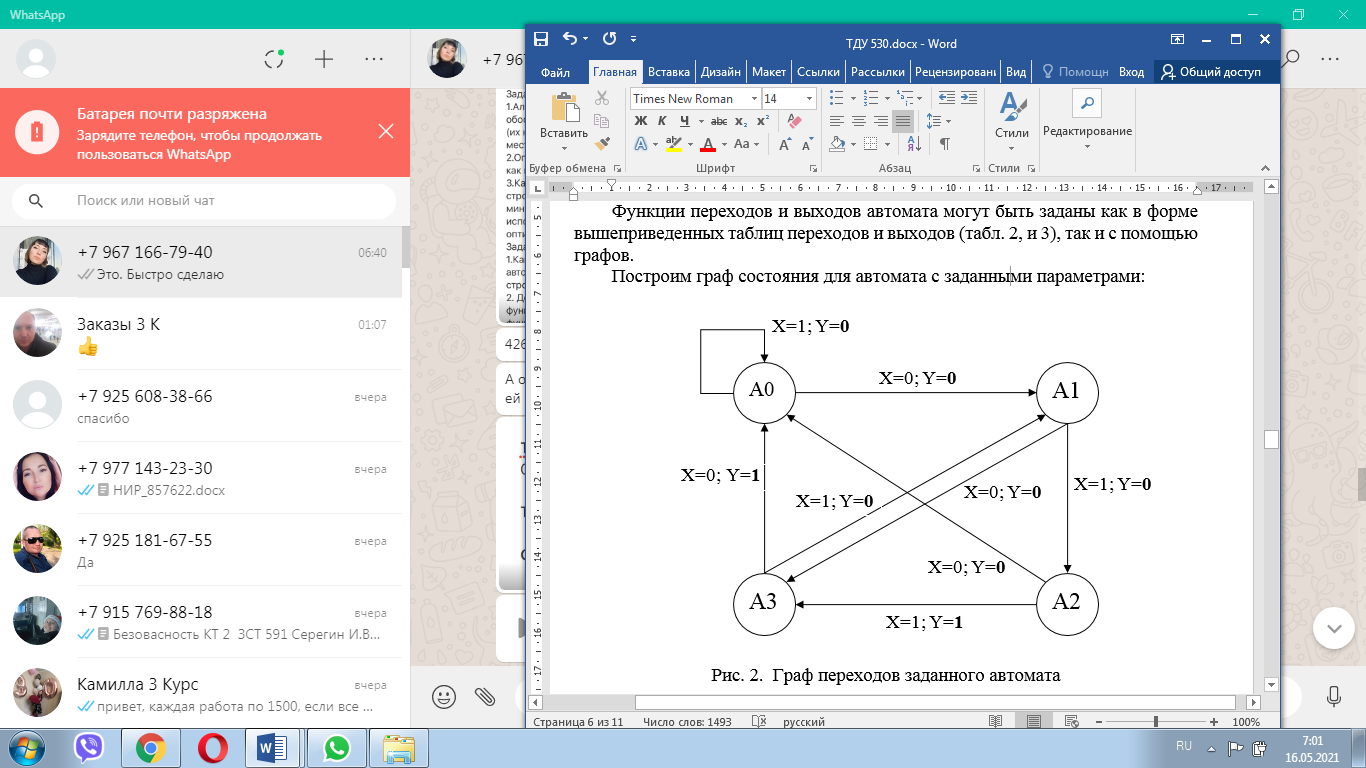 Рис. 2. Граф переходов заданного автомата Задавая произвольную двоичную последовательность (входное слово), определить соответствующую двоичную выходную последовательность (выходное слово) автомата. Пусть автомат находится в состоянии А0 и подано: 11110000. Следовательно:
Выходное слово 0000010, а автомат остановится в состоянии А1. Заполним таблицу 4 фнкционирования автомата, заданного графом, представленным на рисунке 2. Таблица составляется по таблице переходов триггера Таблица переходов RS-триггера
Составим таблицу функционирования автомата Мили (табл. 6). В первых трех столбцах таблицы запишем все возможные сочетания кодов входного сигнала и состояния автомата. Для заданного входного сигнала и состояния автомата по графу найдем значение выходного сигнала, которое запишем в последнем столбце таблицы, и следующее состояние автомата, в которое он переходит. Код этого состояния занесем в четвертый и пятый столбцы таблицы. Столбцы с 6 по 9 отведены для записи сигналов управления триггерами. Их заполним в соответствии с таблицей переходов RS-триггера. В случаях, когда логический уровень сигнала управления безразличен («0» или «1»), в соответствующие клетки занесем символ “”. Табл.4.Таблица функционирования автомата Мили.
Найдем Функции выходного сигнала в ДНФ:  Кодирование состояний автомата может производиться произвольно. Для синтезируемого автомата кодирование его состояний произведем в соответствии табл. 5. Табл.5.Кодирование состояний автомата.
Для построения комбинационного устройства, формирующего сигналы управления триггерами, составим для этих сигналов S2, S1, R2, R1 таблицы истинности в форме карт Карно.  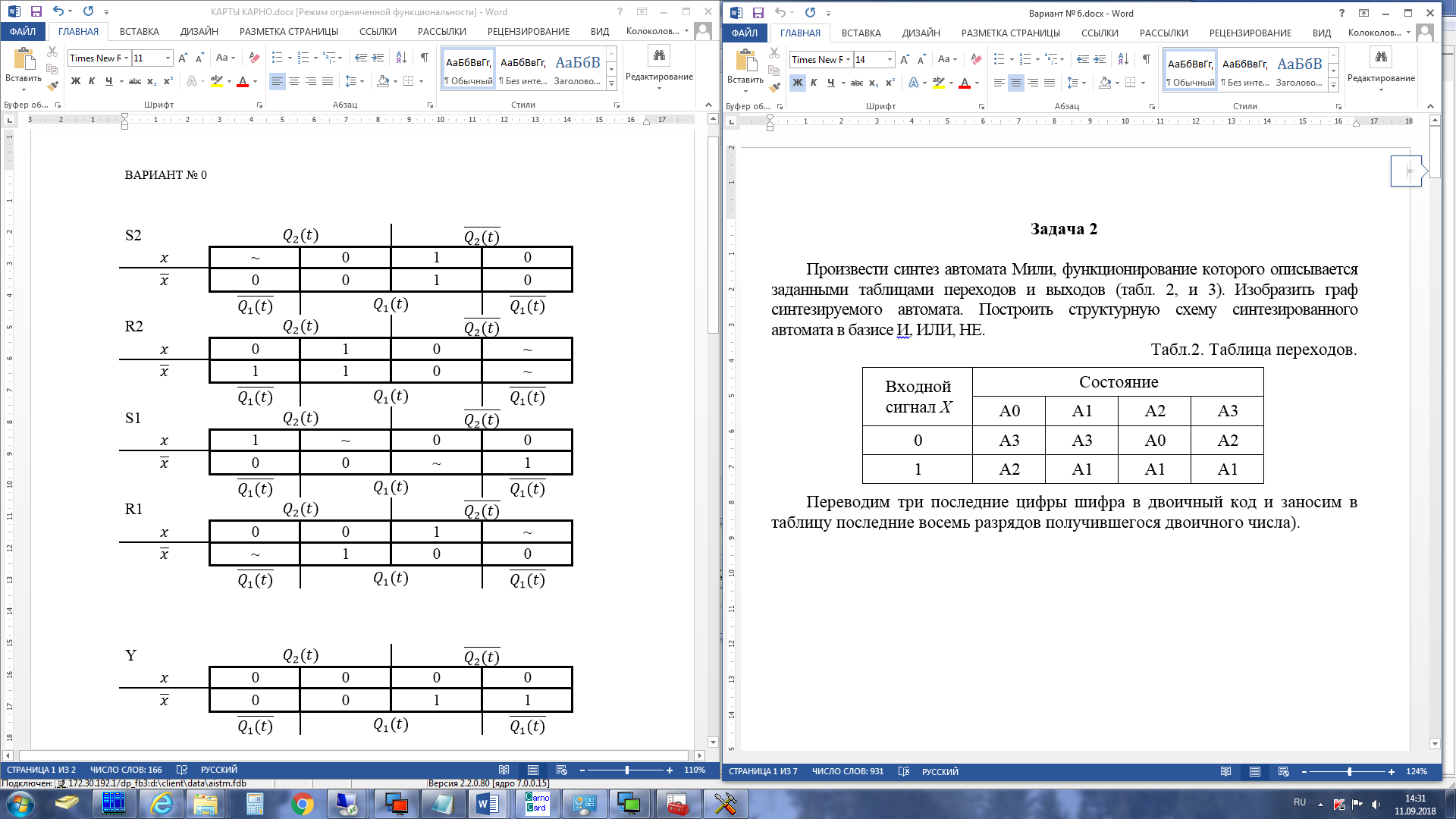 Составим карту Карно для выходного сигнала (Y).     2 1 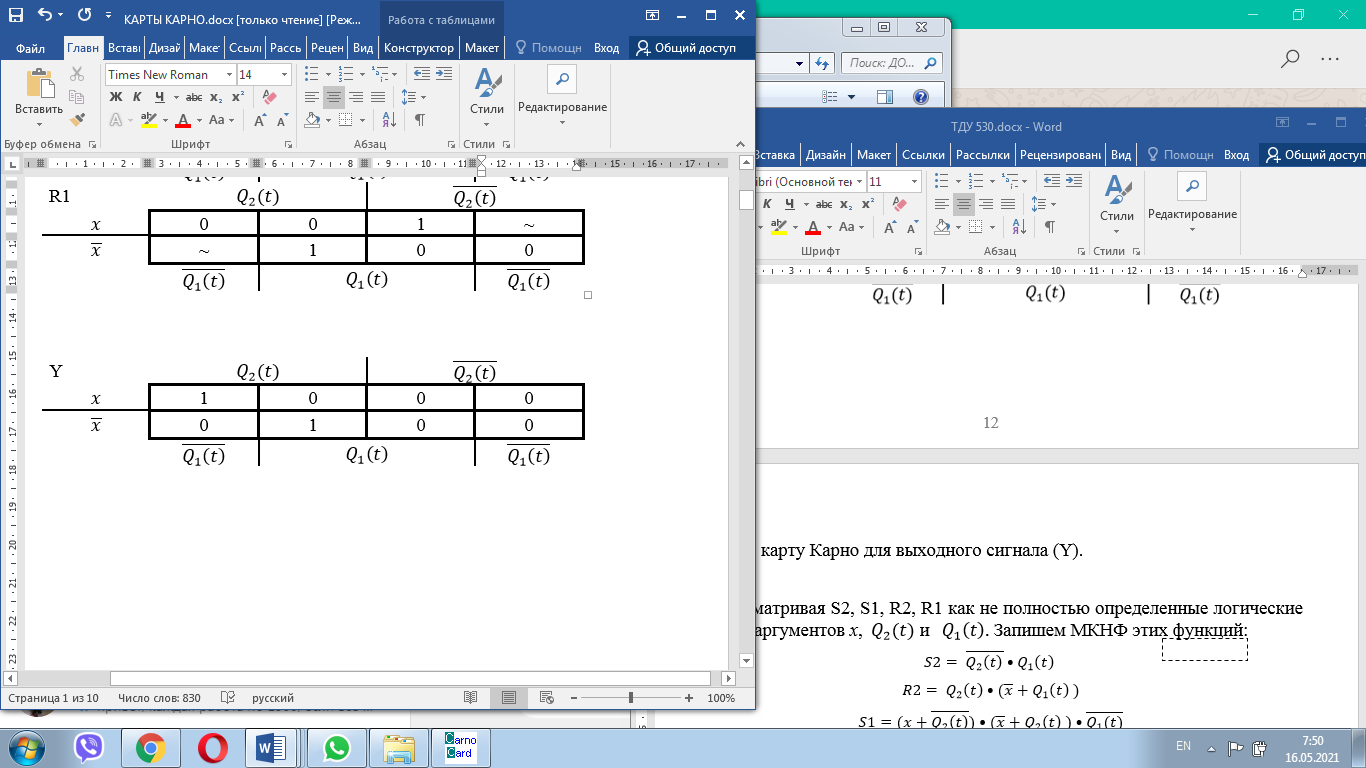 Рассматривая S2, S1, R2, R1 как не полностью определенные логические функции аргументов x, 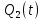 и и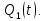 Запишем МКНФ этих функций: Запишем МКНФ этих функций: 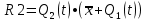 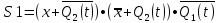  Для построения комбинационного устройства, формирующего выходной сигнал автомата, строим таблицу истинности для y в форме карт Карно: Минимальная ДНФ функции Y: 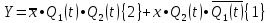 Используя полученные логические выражения и выбрав в качестве базиса логические элементы И, ИЛИ, НЕ, вычерчиваем структурную схему синтезируемого автомата (рис. 3). Для обеспечения правильной работы схемы автомата необходимо предусмотреть синхронизацию ее функционирования во времени, т.е. формирование тактов (временных интервалов) 1,2, ..., t, t+1, ..., во время действия которых осуществляются все логические зависимости. На схеме (рис. 3) предусмотрен сигнал управления Uynp, который в произвольный момент времени: разрешает подачу управляющих сигналов с выхода комбинационного устройства на входы триггеров. При этом триггеры Т1 и Т2 устанавливаются в состояние Q1(t+1), Q2(t+1), в соответствии с заданным таблицей переходов законом функционирования автомата. Однако на время действия сигнала Uупр (такта t) выходы (Q и  ) входных триггеров Т1 и Т2 блокированы группой схем И, на вход каждой из которых поступает сигнал, инверсный Uynp. В то же время группа выходных триггеров Т1^ и Т2^ сохраняют свои состояния Q1(t) и Q2(t), и только их выходные сигналы поступают на входы обеих комбинационных схем и совместно с входным сигналом X определяют логику работы автомата. ) входных триггеров Т1 и Т2 блокированы группой схем И, на вход каждой из которых поступает сигнал, инверсный Uynp. В то же время группа выходных триггеров Т1^ и Т2^ сохраняют свои состояния Q1(t) и Q2(t), и только их выходные сигналы поступают на входы обеих комбинационных схем и совместно с входным сигналом X определяют логику работы автомата.После окончания действия управляющего импульса Uyпp, в течение интервала между тактами tи (t + 1), сигналы с выходов Т1 и Т2 через схемы И, на входы которых уже поступает разрешающий инверсный сигнал Uyпp, подаются на соответствующие входы Т1^ и Т2^, в результате чего последние переходят в состояния Q1(t) и Q2(t). Благодаря наличию в схеме автомата дополнительных триггеров Т1^ и Т2^, сигналы Q1(t) и Q2(t)на входе комбинационного устройства сохраняются в течении всего времени (такта t) действия управляющего импульса.  Рис.3.Структурная схема синтезируемого автомата Список используемой литературы 1. Сапожников В.В., Кравцов Ю.А., Сапожников Вл.В. Теоретические основы железнодорожной автоматики и телемеханики: Учебник для вузов ж-д транспорта/ Под ред. В.В. Сапожникова. М.: ГОУ «Учебно-методический центр по образованию на железнодорожном транспорте», 2008.- 394 с. 2. Сапожников В.В., Кравцов Ю.А., Сапожников Вл.В. Теория дискретных устройств железнодорожной автоматики, телемеханики и связи: Учеб. для вузов ж.-д. трансп./Под ред. В.В. Сапожникова, 2-е изд., перераб. и доп.-М.: УМК МПС России, 2001.-312 с. 3. Горелик В.Ю., Ермаков А.Е., Ермакова О.П. Схемотехника ЭВМ: Учебное пособие для вузов ж-д транспорта.- М.: ГОУ «Учебно-методический центр по образованию на железнодорожном транспорте», 2007.- 174 с. 4. Шалягин Д.В. Теоретические основы автоматики и телемеханики на железнодорожном транспорте: Ч.1. Дискретные автоматы.- М.: РГОТУПС, 1998.-144 с. 5. Пухальский Г.И., Новосельцева Т.Я. Проектирование дискретных устройств на интегральных микросхемах.- М.:Радио и связь, 1990. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||