Практикалық жұмыс 2. Таырып Материялы нктені динамикасы. Тжірибелік саба 2. (1 саат)
 Скачать 4.27 Mb. Скачать 4.27 Mb.
|
|
Тақырып 2. Материялық нүктенің динамикасы. Тәжірибелік сабақ №2 . (1 сағат) Мақсаты: Материялық нүктенің динамикасы тарауының Ньютонның заңдарын және формулаларын білу және есептер шығаруға қолдану. Жоспар: Ньютон заңдары негізгі ұғымдары мен формулалары. Ньютон заңдары. Импульстің сақталу заңының негізгі ұғымдары мен формулалары. Импульстің сақталу заңы. Ньютон заңдары. 1. Материялық нүктенің қозғалыс теңдеуі (Ньютонның екінші заңы): векторлық түрінде 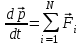 , немесе , немесе 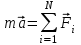 , ,мұндағы 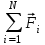 - материялық нүктеге әсер ететін күштердің геометриялық қосындысы; - материялық нүктеге әсер ететін күштердің геометриялық қосындысы; 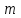 - массасы; - массасы; 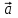 - үдеуі; - үдеуі; 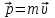 - импульсі; - импульсі; 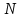 - нүктеге әсер ететін күштердің саны; - нүктеге әсер ететін күштердің саны;координаталық түрінде (скалярлық): 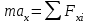 , , 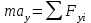 , , 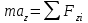 , ,немесе  , , 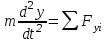 , , 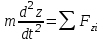 , ,мұнда қосынды таңбасының астында тұрған сәйкес координаталар остеріндегі 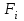 күштерінің проекциялары. күштерінің проекциялары.2. Серпімділік күші: 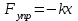 , ,мұндағы 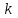 - серпімділік коэффициенті (серіппе болса қатаңдық); - серпімділік коэффициенті (серіппе болса қатаңдық); 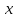 - абсолюттік деформация. - абсолюттік деформация.3. Гравитациялық өзара әсерлесу күші: 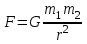 , ,мүндағы 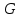 - гравитациялық тұрақты; - гравитациялық тұрақты;  және және 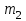 - материялық нүте ретінде қарастырылған әсерлесетін денелердің массалары; - материялық нүте ретінде қарастырылған әсерлесетін денелердің массалары; 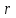 - олардың арақашықтығы. - олардың арақашықтығы.4. Сырғанау үйкеліс күші: 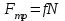 , ,мұндағы 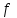 - сырғанау үйкеліс коэффициенті; - сырғанау үйкеліс коэффициенті; 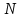 - нормаль қысым күші. - нормаль қысым күші.№1 есеп. Мұз бетінде 2,44 м/с жылдамдықпен сырғанап келе жатқан массасы 1,05 кг тас нйкеліс күшінің әсеренен 10 с - тан кейін тоқтады. Үйкеліс күшін тұрақты деп есептеп, оның мәнін табыңдар. Шешуі: Ньютонның екінші заңы бойынша:  мұндағы 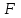 - дененің жылдамдығын - дененің жылдамдығын 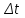 уақыт ішінде уақыт ішінде  - ден - ден 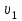 -ге кемітетін үйкеліс күші. Бұл жағдайда -ге кемітетін үйкеліс күші. Бұл жағдайда  болғандықтан болғандықтан 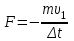 Минус таңбасы үйкеліс күшінің бағыты дененің 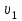 жылдамдығының бағытына қарсы екенін көрсетеді. Сандық мәндерін орнына қоямыз: жылдамдығының бағытына қарсы екенін көрсетеді. Сандық мәндерін орнына қоямыз:  №2 есеп. Біртекті шыбықтың ұштарына қарама-қарсы жаққа бағытталған екі күш түсірілген: 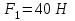 және және 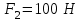 ( ( - сурет). - сурет).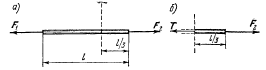 1 - сурет Шыбықты l 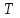 керілу күшін табыңдар. керілу күшін табыңдар.Шешуі: Егер 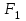 және және 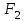 күштері тең болса, онда керілу күші шыбықтың кезкелген қимасында бірдей және шыбықтың ұштарына түсірілген күштерге тең болар еді. Бұл жағдайда шыбық тыныштықта болады. Бірақ біздің жағдайымызда шыбыққа әсер ететін күштердің қосындысы нөлге тең емес. Сондықтан шыбық шамасы мен бағыты Ньютонның екінші заңымен анақталатын үдеумен қозғалады: күштері тең болса, онда керілу күші шыбықтың кезкелген қимасында бірдей және шыбықтың ұштарына түсірілген күштерге тең болар еді. Бұл жағдайда шыбық тыныштықта болады. Бірақ біздің жағдайымызда шыбыққа әсер ететін күштердің қосындысы нөлге тең емес. Сондықтан шыбық шамасы мен бағыты Ньютонның екінші заңымен анақталатын үдеумен қозғалады: 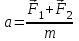 Мұндағы 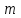 - шыбықтың массасы. Екі күш бір түзудің бойымен бағытталғандықтан геометриялық қосындыны алгебралықпен ауыстыруға болады: - шыбықтың массасы. Екі күш бір түзудің бойымен бағытталғандықтан геометриялық қосындыны алгебралықпен ауыстыруға болады: 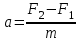 (1) (1)Шыбық үдемелі қозғалған кезде әртүрлі қиадағы керілу күші де әртүрлі болады. Бұл күштерді анықтау үшін мына әдісті қолданамыз: шыбықтың қимасын бізге қажетті екі бөлікке бөлеміз және олардың біреуін алып тастаймыз, мысалы сол жағын. Сол жақ бөлігіндегі әрекетті 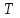 керілу күшімен ауыстырамыз (1б - сурет). керілу күшімен ауыстырамыз (1б - сурет). 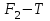 күштері айырымының әсер етуі нәтижесінде массасы күштері айырымының әсер етуі нәтижесінде массасы  -ге тең оң жағы шамасы мен бағыты бойынша бұрынғы үдеуге тең (1) формуладағы үдеумен қозғалады: -ге тең оң жағы шамасы мен бағыты бойынша бұрынғы үдеуге тең (1) формуладағы үдеумен қозғалады: 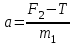 Шыбық біртекті болғандықтан 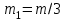 және бұдан және бұдан 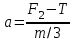 (2) (2)- ші және (2) - ші теңдеулердің оң жақтарын теңестіріп керілу күшін табамыз: 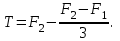 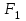 және және 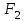 - нің сан мәндерін қоямыз: - нің сан мәндерін қоямыз: 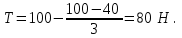 №3 есеп. Лифтің ішінде серіппелі таразыда массасы 10 кг дене бар (2-сурет). Лифт 2м/с2 үдеумен қозғалады. Екі жағдай үшін таразының көрсетуін табыңдар: 1) лифт тік жоғары көтерілгенде; 2) лифт тік төмен түскенде. 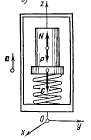 Шешуі: Таразының көрсетуін табу - бұл дененің салмағын табу, яғни дененің серіппеге әсер ету күшін. Бұл күш Ньютонның үшінші заңы бойынша 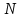 серпімділік күшіне (тіректің реакция күшіне) модулі бойынша тең, ал бағыты бойынша қарама-қарсы. серпімділік күшіне (тіректің реакция күшіне) модулі бойынша тең, ал бағыты бойынша қарама-қарсы.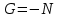 немесе немесе 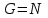 (1) (1)Демек, таразының көрсетуін табу дегеніміз тректің N реакция күшін табу. Денеге екі күш әсер етеді: ауырлық күші Р және N тректің реакция күші (қысым күші). z осін тік жоғары қарай бағыттап және оған денеге әсер ететін барлық күштердің проекциясын түсірейік. Күштерді бағыттары бойынша оң және теріс таңбамен аламыз. z осімен бағыттас күштерді - оң, ал оған қарсыны - теріс. Ньютонның екінші заңын жазайық: 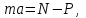 бұдан бұдан 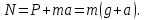 (2) (2)(1) - ші және (2) - ші теңдеулерден 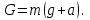 Таразының көрсетулерін есептеген кезде үдеудің таңбасын ескеру керек: Үдеу тік жоғары бағытталған 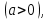 демек демек 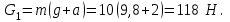 Үдеу тік төмен бағытталған 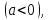 демек демек 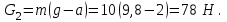      Импульстің сақталу заңы. 1. Материялық нүктенің қозғалыс теңдеуі (Ньютонның екінші заңы): векторлық түрінде 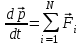 , немесе , немесе 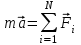 , ,мұндағы 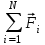 - материялық нүктеге әсер ететін күштердің геометриялық қосындысы; - материялық нүктеге әсер ететін күштердің геометриялық қосындысы; 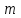 - массасы; - массасы; 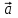 - үдеуі; - үдеуі; 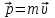 - импульсі; - импульсі; 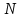 - нүктеге әсер ететін күштердің саны; - нүктеге әсер ететін күштердің саны;координаталық түрінде (скалярлық): 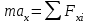 , , 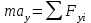 , , 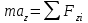 , ,немесе  , , 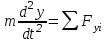 , , 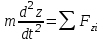 , ,мұнда қосынды таңбасының астында тұрған сәйкес координаталар остеріндегі 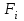 күштерінің проекциялары. күштерінің проекциялары.2. Серпімділік күші: 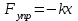 , ,мұндағы 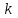 - серпімділік коэффициенті (серіппе болса қатаңдық); - серпімділік коэффициенті (серіппе болса қатаңдық); 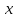 - абсолюттік деформация. - абсолюттік деформация.3. Гравитациялық өзара әсерлесу күші: 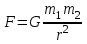 , ,мүндағы 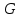 - гравитациялық тұрақты; - гравитациялық тұрақты;  және және 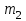 - материялық нүте ретінде қарастырылған әсерлесетін денелердің массалары; - материялық нүте ретінде қарастырылған әсерлесетін денелердің массалары; 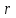 - олардың арақашықтығы. - олардың арақашықтығы.4. Сырғанау үйкеліс күші: 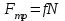 , ,мұндағы 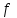 - сырғанау үйкеліс коэффициенті; - сырғанау үйкеліс коэффициенті; 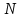 - нормаль қысым күші. - нормаль қысым күші.5. Импульстің сақталу заңы: 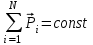 немесе немесе 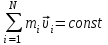 мұндағы 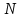 - жүйеге енетін материялық нүктелердің (немесе денелердің) саны. - жүйеге енетін материялық нүктелердің (немесе денелердің) саны.6. Шарлардың тура орталық соққысына энергия мен импульстің сақталу заңын қолданып, шарлардың абсолют серпімсіз соққыдан кейінгі жылдамдығының формуласын:  , ,және шарлардың абсолют серпімді соққыдан кейінгі жылдамдығының формуласын: 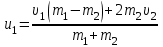 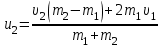 аламыз. аламыз.мұндағы  және және 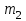 - шарлардың массалары; - шарлардың массалары; 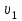 және және  - олардың соқтығысқанға дейінгі жылдамдықтары. - олардың соқтығысқанға дейінгі жылдамдықтары.№1 есеп. Массасы 64 кг адам мен массасы 32 кг арба бір-біріне қарсы қозғалады. Адамның жылдамдығы 5,4 км/сағ, арбаның жылдамдығы 1,8 км/сағ.Адам арбаға секіріп мінгендегі арба мен адамның жылдамдығын табыңдар. Шешуі: Импульстің сақталу заңы бойынша: 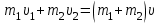 (1) (1)Мұндағы  - адамның массасы; - адамның массасы; 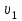 - адамның бастапқы жылдамдығы; - адамның бастапқы жылдамдығы; 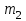 - арбаның массасы; - арбаның массасы;  - арбаның бастапқы жылдамдығы; - арбаның бастапқы жылдамдығы; 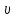 - адам мен арбаның жалпы жылдамдығы. - адам мен арбаның жалпы жылдамдығы.- ші өрнектен  Адам мен арбаның бастапқы жылдамдықтарының бағыттары қарсы болғандықтан, олардың жылдамдықтарының таңбалары да әр-түрлі болады. Адамның жылдамдығының бағыты оң деп алынса, арбаның жылдамдығының бағыты теріс болады. Сонда 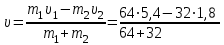 = 3,0 км/сағ = 0,83 м/с. = 3,0 км/сағ = 0,83 м/с.№2 есеп. Массасы 0,3 кг шар, 10 м/с жылдамдықпен қозғалып, қозғалмайтын тегіс қабырғаға жылдамдығы нормальмен 300 бұрыш жасап серпімді соқтығысады. Қабырғаның алатын р импульсін анықтаңдар. Шешуі: Алдымен есептің шартын талдайық. Қабырға қозғалмайды, сондықтан онымен байланысқан санақ жүйесі инерциалды болады. Шардың қабырғаға соқтығысуы серпімді, демек импульстің сақталу заңын қолданамыз. Қабырғаның массасы шардыкінен өте үлкен болғандықтан шардың соқтығысқанға дейінгі  және кейінгі және кейінгі  жылдамдықтарының модулдері тең болады. жылдамдықтарының модулдері тең болады.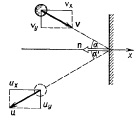 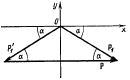 1-сурет 2-сурет Шардың қабырғадан шағылу бұрышы  шардың түсу шардың түсу  бұрышына тең болады. υ және u векторларының Ох және Оу остеріне проекцияларын түсіреміз (1-сурет). Қабырға тегіс болғандықтан бұрышына тең болады. υ және u векторларының Ох және Оу остеріне проекцияларын түсіреміз (1-сурет). Қабырға тегіс болғандықтан 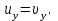  екенін ескерсек , екенін ескерсек , 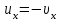 аламыз, бұдан түсу және шағылу бұрыштарының тең екені шығады аламыз, бұдан түсу және шағылу бұрыштарының тең екені шығады  . . Қабырғаның алған импульсін анықтау үшін импульстің сақталу заңын қолданамыз. Біздің жағдайда бұл заң былай жазылады: 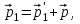 мұндағы  және және 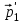 - шардың соқтығысқанға дейінгі және кейінгі импульстері. Бұдан қабырғаның алған импульсі: - шардың соқтығысқанға дейінгі және кейінгі импульстері. Бұдан қабырғаның алған импульсі:  2-суреттен көріп тұрғанымыз  векторы Ох осімен бағыттас және оның модулі: векторы Ох осімен бағыттас және оның модулі: 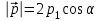 Осы формуладағы 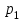 - дің орнына импульстің - дің орнына импульстің 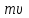 өрнектегіy қоямыз: өрнектегіy қоямыз: 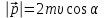 Сан мәндерін орындарына қоямыз:  №3 есеп. Тоғанның тыныш суында ұзындығы 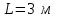 және массасы және массасы 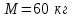 жағаға перпендикуляр оған тұмсығымен қарап қайық тұр. Қайықтың артқы жағында массасы жағаға перпендикуляр оған тұмсығымен қарап қайық тұр. Қайықтың артқы жағында массасы 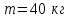 адам тұр. Егер адам қайықтың артынан тұмсығына келсе, қайық жағаға қандай адам тұр. Егер адам қайықтың артынан тұмсығына келсе, қайық жағаға қандай  қашықтыққа жақындайды. қашықтыққа жақындайды.Шешуі: Қайықтағы адам тұрақты жылдамдықпен қозғалсын. Бұл жағдайда қайықта бірқалыпты қозғалады. Сондықтан қайықтың жағаға қатысты орынауыстыруын мына формуламен табамыз:  (1) (1)мұндағы 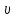 - қайықтың жағаға қатысты жылдамдығы; - қайықтың жағаға қатысты жылдамдығы; 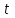 - адам мен қайықтың қозғалыс уақыты. Адамның орынауыстыруының бағытын оң деп алайық. - адам мен қайықтың қозғалыс уақыты. Адамның орынауыстыруының бағытын оң деп алайық.Қайықтың 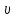 жылдамдығын импульстің сақталу заңынан табамыз. Есептің шарты бойынша адам – қайық жүйесі бастапқы мезетте жағаға қатысты тыныштықта болады, онда импульстің сақталу заңы бойынша: жылдамдығын импульстің сақталу заңынан табамыз. Есептің шарты бойынша адам – қайық жүйесі бастапқы мезетте жағаға қатысты тыныштықта болады, онда импульстің сақталу заңы бойынша:  мұндағы 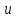 - адамның жағаға қатысты жылдамдығы; минус таңбасы адам мен қайықтың жылдамдықтары бағыттары бойынша қарама-қарсы екенін көрсетеді. Бұдан - адамның жағаға қатысты жылдамдығы; минус таңбасы адам мен қайықтың жылдамдықтары бағыттары бойынша қарама-қарсы екенін көрсетеді. Бұдан 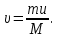 Қайықтың қозғалыс уақыты 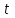 адамның қайықпен орынауыстырғандағы уақытына тең, яғни адамның қайықпен орынауыстырғандағы уақытына тең, яғни 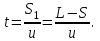 мұндағы 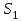 - адамның жағаға қатысты орынауыстыруы. - адамның жағаға қатысты орынауыстыруы.Жылдамдық 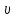 - мен уақыт - мен уақыт 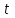 - ның өрнектерін (1) формулаға қоямыз: - ның өрнектерін (1) формулаға қоямыз: осыдан осыдан 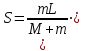 Сан мәндерін орындарына қоямыз: 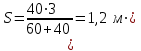 №4 есеп. Массалары 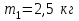 және және 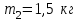 екі шар бір - біріне қарсы екі шар бір - біріне қарсы 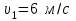 және және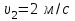 жылдамдықпен қозғалады. Мыналарды табыңда: 1) соқтығысқаннан кейінгі шарлардың жылдамдықпен қозғалады. Мыналарды табыңда: 1) соқтығысқаннан кейінгі шарлардың 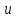 жылдамдығын; 2) соқтығысқанға дейінгі және соқтығысқаннан кейінгі шарлардың жылдамдығын; 2) соқтығысқанға дейінгі және соқтығысқаннан кейінгі шарлардың 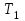 және және  кинетикалық энергияларын; 3) ішкі энергияға айналған шарлардың кинетикалық энергиясының кинетикалық энергияларын; 3) ішкі энергияға айналған шарлардың кинетикалық энергиясының 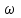 үлесін. Соққыны тура және серпімсіз деп есептеңдер. үлесін. Соққыны тура және серпімсіз деп есептеңдер.Шешуі: Серпімсіз шарлар соқтығысқаннан кейін өзінің бастапқы пішініне қайта келмейді. Демек шарларда бір-бірінен тебілетін күштер пайда болмайды және шарлар соқтығысқаннан кейін бірдей 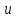 жылдамдықпен қозғалады. Бұл жылдамдықты импульстің сақталу заңымен анықтаймыз. Шарлар бір түзудің бойымен қозғалатындықтан, бұл заңды скаляр түрде былай жазамыз: жылдамдықпен қозғалады. Бұл жылдамдықты импульстің сақталу заңымен анықтаймыз. Шарлар бір түзудің бойымен қозғалатындықтан, бұл заңды скаляр түрде былай жазамыз: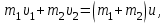 бұдан бұдан 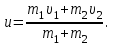 Бірінші шардың жылдамдығының бағытын оң деп алайық, сонда есептеген кезде екінші шардың жылдамдығын қарсы қозғалғандықтан минуспен алу керек: 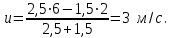 Соқтығысқанға дейінгі және соқтығысқаннан кейінгі шарлардың кинетикалық энергияларын мына формулалармен табамыз:  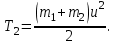 Сан мәндерін орындарына қойып есептейміз: 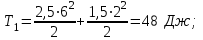 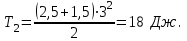 Соқтығысқанға дейінгі және соқтығысқаннан кейінгі шарлардың кинетикалық энергияларын салыстыратын болсақ, шарлардың серпімсіз соқтығысуының нәтижесінде олардың кинетикалық энергияларының кемитінін, осының есебінен ішкі энергияның артатынын көреміз. Ішкі энергияның артуына кеткен шарлардың кинетикалық энергиясының үлесін мына қатынаспен анықтаймыз: 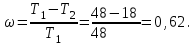 Есептер:       |
