Б3-31, порядковый 17. Техническая механика
 Скачать 370.88 Kb. Скачать 370.88 Kb.
|
|
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное государственное образовательное учреждение высшего образования «Саратовский государственный технический университет имени Гагарина Ю.А.» Кафедра: «Техническая механика и мехатроника» (ТММ) Расчетно-графическая работа По дисциплине «Техническая механика» Выполнил студент группы: Б3 -НФГДозипу-31 ААААААА Б.С. Шифр: 111222 Проверил: ст. преподаватель каф. ТММ: Пименов Д.А. Саратов 2022 СОДЕРЖАНИЕ
Лист заданияСогласно порядковому номеру студента по списку в журнале приняты следующие входные данные:
Согласно номеру группы (Б3 -НФГДозипу-31) приняты:  расчетный коэффициент для сосредоточенных сил – 1,6; расчетный коэффициент для сосредоточенных сил – 1,6; расчетный коэффициент для интенсивности распределения снеговой нагрузки – 1,1; расчетный коэффициент для интенсивности распределения снеговой нагрузки – 1,1; расчетный коэффициент для собственного веса – 2,0; расчетный коэффициент для собственного веса – 2,0; начальное сечение – (50×50)мм. начальное сечение – (50×50)мм.Согласно нормативам климатического распределения, при II снеговом районе нормативная нагрузка на квадратный метр будет равной 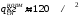 , соответственно нормативная погонная интенсивность распределения снеговой нагрузка будет равна произведению шага балочной конструкции на интенсивность распределения снеговой нагрузки на квадратный метр, т.е.: , соответственно нормативная погонная интенсивность распределения снеговой нагрузка будет равна произведению шага балочной конструкции на интенсивность распределения снеговой нагрузки на квадратный метр, т.е.: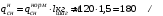 . .Расчетная интенсивность распределения снеговой нагрузки равна: 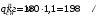 . .Расчетные значения сосредоточенных сил равны: 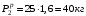 ; ; 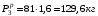 . . Поскольку по условию 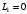 , следовательно сила , следовательно сила 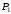 не нагружает балку в пролете и поэтому данную силу в расчетах не учитываем. не нагружает балку в пролете и поэтому данную силу в расчетах не учитываем.Расчетное сопротивление изгибу примем равным 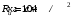 , расчетное сопротивление скалыванию вдоль волокон , расчетное сопротивление скалыванию вдоль волокон  . Объемный вес для породы липа . Объемный вес для породы липа 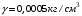 ; модуль упругости при изгибе ; модуль упругости при изгибе 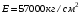 . Погонная нагрузка от собственного веса равна: . Погонная нагрузка от собственного веса равна: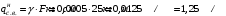 ; ;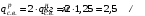 . .Здесь  – поперечное сечение балки. – поперечное сечение балки.1. Положение декартовой системы координатПоскольку поперечное сечение балки (квадрат) имеет две оси симметрии (оси х и у на рисунке 1), то центр тяжести сечения расположен в точке пересечения этих осей. 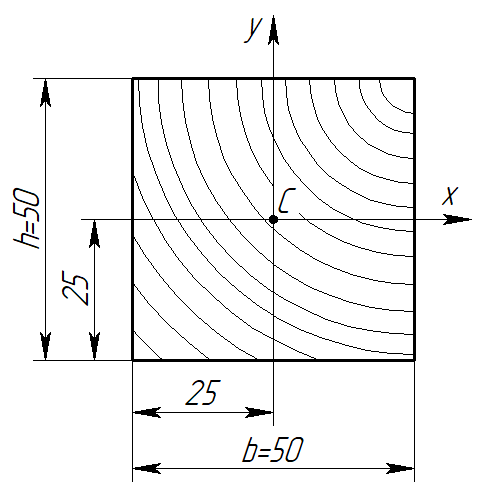 Рисунок 1 – Положение системы координат 2. Статическая определимость балочной конструкцииПо условию задачи, балочная конструкция закреплена по обоим концам шарнирно. Причем, левый конец будет шарнирно неподвижной опорой, а правый станет шарнирно подвижной (рисунок 2). Балка однопролетная.  Рисунок 2 – Статическая определимость балки В таком случае конструкция является статической определимой, так как на балку наложено три ограничения, а независимых уравнений равновесия для плоской системы сил можно также составить три. 3. Основные геометрические характеристики поперечного сеченияCтатический момент полусечения (рисунок 1): 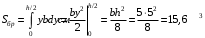 . .Высота и ширина балочной конструкции по условию равны 5 сантиметров . Момент инерции поперечного сечения балки (рисунок 1) определим по формуле: 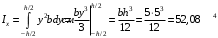 . .Центробежный моменты инерции сечения равен нулю, так как сечение имеет оси симметрии. Далее определим момент сопротивления сечения формуле: 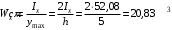 . .4. Определение опорных реакцийРасчетная схема балки показана на рисунке 3. На балку действуют три сосредоточенные силы 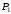 , , 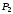 и и 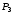 , равномерно распределенная нагрузка от собственного веса , равномерно распределенная нагрузка от собственного веса 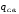 и равномерно распределенная снеговая нагрузка и равномерно распределенная снеговая нагрузка 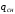 . Реакцию шарнирно неподвижной опоры 1 представляем двумя составляющими: вертикальной . Реакцию шарнирно неподвижной опоры 1 представляем двумя составляющими: вертикальной 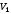 и горизонтальной и горизонтальной 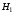 . Реакцию шарнирно подвижной опоры 2 . Реакцию шарнирно подвижной опоры 2 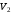 направлена перпендикулярно опорной плоскости, т.е. вертикально. направлена перпендикулярно опорной плоскости, т.е. вертикально.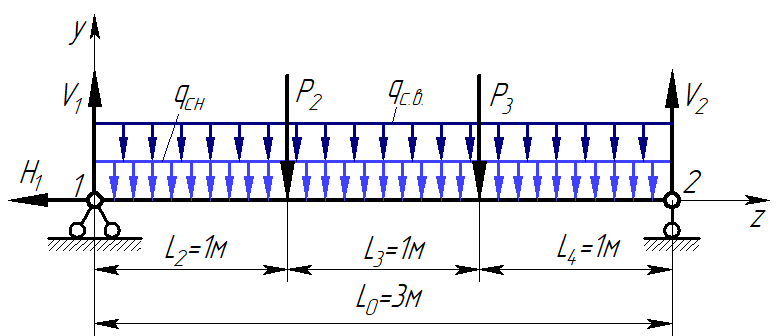 Рисунок 3 – Расчетная схема к определению опорных реакций Для полученной плоской системы сил составляем три уравнения равновесия. 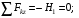 (1) (1)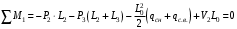 ; (2) ; (2) 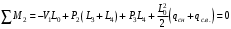 . (3) . (3) Из уравнения (1) : 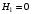 . .Из уравнения (3) : 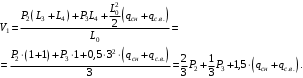 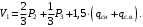 (4) (4)Из уравнения (2) : 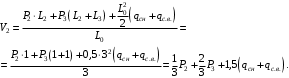 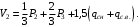 (5) (5)Проверка: 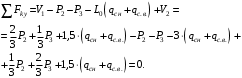 5. Корректировка поперечного сечения балки из условия прочностиРасчет из условий прочности (по несущей способности) должен производиться на воздействие расчетных нагрузок. Поэтому в ранее полученные выражения (4) и (5) подставляем значения расчетных нагрузок и определяем величины реакций опор. 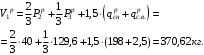 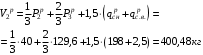 Расчетная схема балки показана на рисунке 4,а. Балку разбиваем на три участка, для каждого из участков запишем выражения для поперечных (перерезывающих) сил 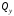 и изгибающих моментов и изгибающих моментов 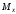 и определим значения этих сил в характерных сечениях. и определим значения этих сил в характерных сечениях.Участок I, 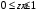 : :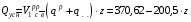 ; ;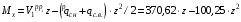 ; ;при  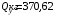 , , 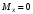 ; ;при 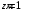 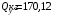 , , 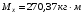 . .Участок II, 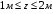 : :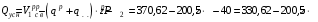 ; ;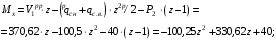 при 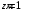 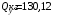 , , 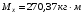 ; ;при 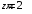 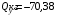 , , 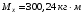 . .Так как на участке II поперечная сила меняет знак, то на эпюре изгибающего момента имеет место экстремум, положение которого определим из условия: 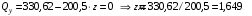 . .При 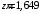 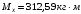 . .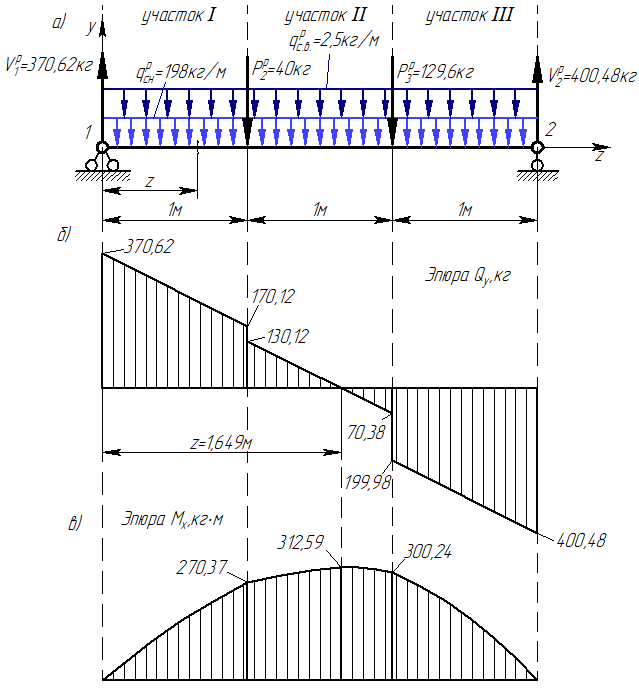 Рисунок 4 – Расчетная схема к определению внутренних силовых факторов Участок III, 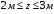 : :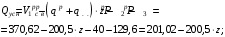 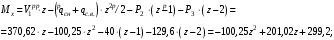 при при 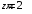 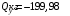 , , 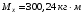 ; ;при 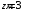 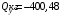 , ,  . .Эпюры поперечных сил и изгибающих моментов показаны на рисунке 4,б и 4,в. Из эпюры изгибающих моментов находим максимальный изгибающий момент, который равен: 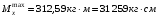 . .Условие прочности изгибаемых элементов: 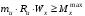 , ,где 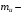 коэффициент условий работы, для бруса с размерами сечения коэффициент условий работы, для бруса с размерами сечения менее 15 см  ; ;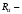 расчетное сопротивление изгибу, расчетное сопротивление изгибу, 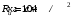 ; ;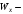 момент сопротивления рассматриваемого поперечного сечения; момент сопротивления рассматриваемого поперечного сечения;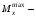 расчетный изгибающий момент, расчетный изгибающий момент, 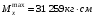 . .Требуемый из условия прочности момент сопротивления поперечного сечения равен: 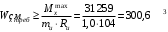 . .Момент сопротивления заданного сечения составляет 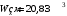 , что существенно меньше требуемого значения. Примем отношение высоты балки к ширине равным , что существенно меньше требуемого значения. Примем отношение высоты балки к ширине равным 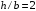 , тогда осевой момент сопротивления для прямоугольного сечения равен: , тогда осевой момент сопротивления для прямоугольного сечения равен: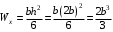 . .Тогда требуемая из условия прочности ширина поперечного сечения балки равна: 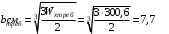 . .Примем  , тогда высота сечения будет равна , тогда высота сечения будет равна 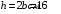 . .Осевой момент сопротивления для принятого сечения равен: 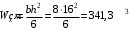 . .Момент инерции для принятого сечения равен: 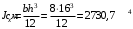 . .Статический момент полусечения для принятого сечения равен: 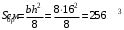 . .Так как высота сечения больше 15 см, то коэффициент условий работы, для бруса с размерами сечения более 15 см и соотношением сторон 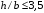 будет равен будет равен 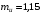 . Проверим выполнение условия прочности: . Проверим выполнение условия прочности: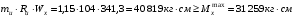 . .Условие прочности на изгиб выполняется. Условие прочности на скалывание: 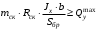 , ,где 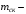 коэффициент условий работы на скалывание при изгибе, коэффициент условий работы на скалывание при изгибе, 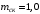 ; ;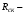 расчетное сопротивление на скалывание, расчетное сопротивление на скалывание,  ; ;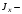 момент инерции поперечного сечения, момент инерции поперечного сечения, 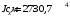 ; ;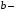 ширина сечения, ширина сечения,  ; ;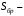 статический момент полусечения, статический момент полусечения,  ; ;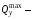 расчетная поперечная сила, расчетная поперечная сила, 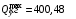 . .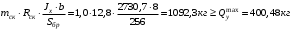 . .Условие прочности на скалывание выполняется. 6. Корректировка поперечного сечения балки из условия устойчивостиРасчет из условий устойчивости (расчет по деформациям) должен производиться на воздействие нормативных нагрузок. Поэтому в ранее полученные выражения (4) и (5) подставляем значения нормативных нагрузок и определяем величины реакций опор. 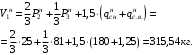  Расчетная схема балки показана на рисунке 5,а. 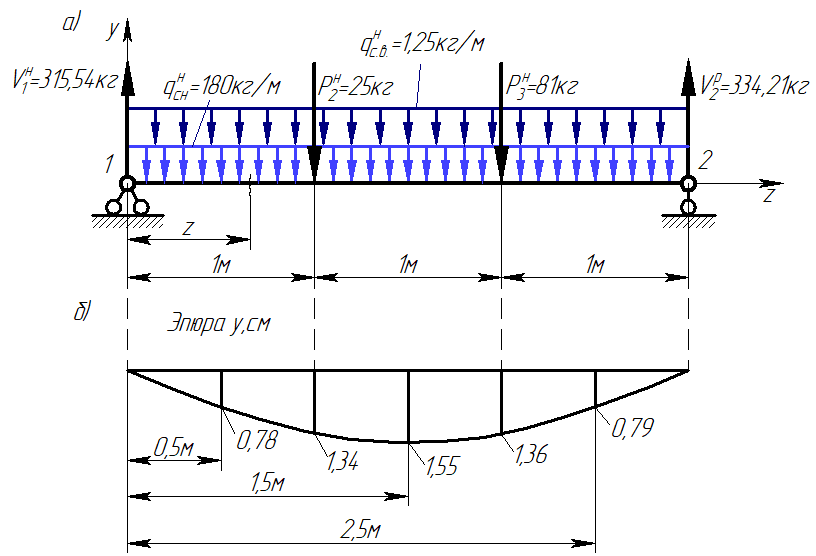 Рисунок 5 – Расчетная схема к определению величин прогибов балки С помощью метода начальных параметров найдем линейные перемещения сечений балки с принятым поперечным сечением в виде прямоугольника (8×16)см и построим эпюру этих перемещений. Составим уравнение метода начальных параметров для прогиба в опоре 2: 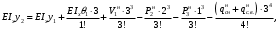 где 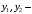 прогибы балки в опорах 1 и 2; прогибы балки в опорах 1 и 2;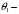 поворот сечения в опоре 1; поворот сечения в опоре 1;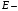 модуль продольной упругости, модуль продольной упругости, 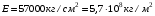 ; ;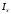 – осевой момент инерции поперечного сечения балки, – осевой момент инерции поперечного сечения балки, 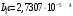 ; ;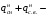 равномерно распределенная нагрузка, равномерно распределенная нагрузка, 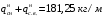 ; ;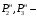 сосредоточенные силы, сосредоточенные силы, 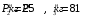 ; ;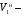 реакция опоры 1, реакция опоры 1, 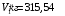 . .Так как 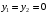 (прогибы в опорах 1 и 2 равны нулю), то получим: (прогибы в опорах 1 и 2 равны нулю), то получим: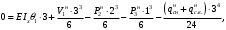 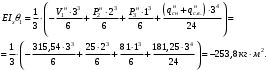 Для построения эпюр линейных перемещений сечений вычислим пять ординат в пролете балки, используя уравнение метода начальных параметров. При 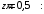 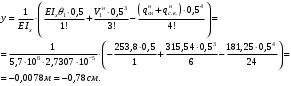 При 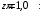 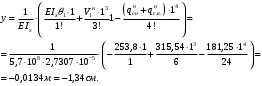 При 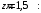 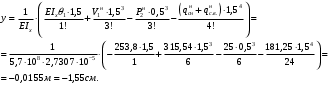 При 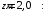 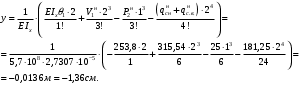 При 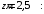 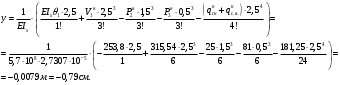 Эпюра линейных перемещений сечений балки показана на рисунке 5,б. Из эпюры линейных перемещений сечений балки определяем величину максимального прогиба: 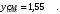 Максимально допустимая величину прогиба балки равна 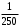 от общей длины балки, т.е. равна от общей длины балки, т.е. равна 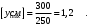 Поскольку Поскольку 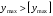 , условие жесткости не выполняется. В таком случае определим требуемое значение осевого момента инерции поперечного сечения балки. , условие жесткости не выполняется. В таком случае определим требуемое значение осевого момента инерции поперечного сечения балки.Так как величина прогиба обратно пропорциональна значению осевого момента инерции поперечного сечения балки, следовательно требуемое из условия жесткости значение этого параметра будет равно: 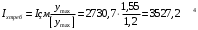 . . Момент инерции принятого при расчете на прочность сечения составляет 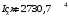 , что меньше требуемого из условия жесткости значения. При отношение высоты балки к ширине равном , что меньше требуемого из условия жесткости значения. При отношение высоты балки к ширине равном 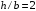 осевой момент инерции для прямоугольного сечения равен: осевой момент инерции для прямоугольного сечения равен: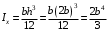 . .Тогда требуемая из условия жесткости ширина поперечного сечения балки равна: 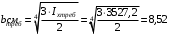 . .Примем 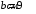 , тогда высота сечения будет равна , тогда высота сечения будет равна 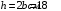 . .Таким образом, окончательные размеры поперечного сечения балки равны: 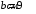 и и 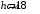 . .7. Заключение по работеВ процессе выполнения задания были усвоены следующие разделы: расчет и подбор геометрических характеристик прямоугольного сечения конструкции; разобраны методики расчета изгибаемых элементов по группам предельных состояний, а именно расчет на первую группу расчетную и на вторую группу нормативную. В процессе расчета были рассмотрены несколько вариантов изменения механических характеристик конструкции и предложены оптимальные пути решения поставленных задач. Список литературы1. СНиП II-25-80.1982. Деревянные конструкции. 2. Сборник задач по сопротивлению материалов: Учеб. пособие для вузов / Н. М. Беляев, Л. К. Паршин, Б. Е. Мельников и др.; под ред. Л. К. Паршина. - СПб. : Изд-во "Иван - 432 с. : ил. ; 21 см. |
