Билеты теплофизика. билеты по теплофизике. Техническая термодинамика цели и задачи. Основные понятия и определения рабочее тело, термодинамическая система (тдс), виды тдс

• Название: Техническая термодинамика цели и задачи. Основные понятия и определения рабочее тело, термодинамическая система (тдс), виды тдс
• Анкор: Билеты теплофизика
• Дата: 15.01.2023
• Размер: 1.23 Mb.
• Имя файла: билеты по теплофизике.doc
• Тип: Закон; #886945
• страница: 1 из 6

1. 
   Техническая термодинамика: цели и задачи. Основные понятия и определения: рабочее тело, термодинамическая система (ТДС), виды ТДС.
   

Термодинамика изучает законы превращения энергии в различных процессах, происходящих в макроскопических системах и сопровождающихся тепловыми эффектами.

Макроскопическая система – любой материальный объект, состоящий из большого числа частиц.

Техническая термодинамика – изучает закономерности взаимного превращения тепловой и механической энергии и свойства тел, участвующих в этих превращениях.

ТДС – представляет собой совокупность материальных тел находящихся в мех-ом и тепловом взаимодействии друг с другом и с внешней средой.

В самом общем случае ТДС может обмениваться со средой и веществом, такая ТДС называется открытой.

ТДС которая не может обмениваться с окружающей средой, называют теплоизолированной или адиабатной.

ТДС не обменивающаяся с внешней средой ни теплом, ни веществом, называется изолированной.

Простейшей ТДС является рабочее тело, осуществляющее взаимное превращение теплоты и работы.

2. 
   Основные параметры состояния: температура
   

Температурой называется фи­зическая величина, характеризующая степень нагретости тела. Понятие о тем­пературе вытекает из следующего утвер­ждения: если две системы находятся в тепловом контакте, то в случае нера­венства их температур они будут обмени­ваться теплотой друг с другом, если же их температуры равны, то теплообмена не будет.

С точки зрения молекулярно-кинетических представлений температура есть мера интенсивности теплового движения молекул. Ее численное значение связано с величиной средней кинетической энер­гии молекул вещества:

, (1.2)

где k— постоянная Больцмана, равная 1,380662•10ˉ²³ Дж/К. Температура T, определенная таким образом, называет­ся абсолютной.

В системе СИ единицей температуры является кельвин (К); на практике широ­ко применяется градус Цельсия (°С). Со­отношение между абсолютной Т и стогра­дусной Iтемпературами имеет вид

.

В промышленных и лабораторных ус­ловиях температуру измеряют с по­мощью жидкостных термометров, пиро­метров, термопар и других приборов.
3. Основные параметры состояния: давление.

Давление обусловлено взаимо­действием молекул рабочего тела с по­верхностью и численно равно силе, дей­ствующей на единицу площади повер­хности тела по нормали к последней. В соответствии с молекулярно-кинетической теорией давление газа определяется соотношением

, (1.1)

где n — число молекул в единице объема;

т — масса молекулы; с²— сред­няя квадратическая скорость поступательного движения молекул.

В Международной системе единиц (СИ) давление выражается в паскалях (1 Па=1 Н/м²). Поскольку эта едини­ца мала, удобнее использовать 1 кПа = 1000 Па и 1 МПа=10⁶ Па.

Давление измеряется при помощи манометров, барометров и вакуумметров.

Жидкостные и пружинные манометры измеряют избыточное давление, пред­ставляющее собой разность между пол­ным или абсолютным давлением р изме­ряемой среды и атмосферным давлением pатм, т.е.

Приборы для измерения давлений ниже атмосферного называются вакуум­метрами; их показания дают значение разрежения (или вакуума):

, т. е. избыток атмосферного давления над абсолютным.

Следует отметить, что параметром состояния является абсолютное давле­ние. Именно оно входит в термодинами­ческие уравнения.
4.Основные параметры состояния: объем.

Удельныйобъемv— это объем единицы массы вещества. Если однородное тело массой М занимает объем v, то по определению

v= V/М.

В системе СИ единица удельного объема 1 м³/кг. Между удельным объемом вещества и его плотность существует очевидное соотношение:



Для сравнения величин, характери­зующих системы в одинаковых состояни­ях, вводится понятие «нормальные физи­ческие условия»:

p=760 мм рт.ст.= 101,325 кПа; T=273,15 K.

В разных отраслях техники и разных странах вводят свои, несколько отличные от приведенных «нормальные условия», например, «технические» ( p= 735,6 мм рт.ст.= 98 кПа , t=15˚C) или нормальные условия для оценки производительности компрессоров (p=101,325 кПа, t=20˚С ) и т. д.

Если все термодинамические пара­метры постоянны во времени и одинако­вы во всех точках системы, то такое состояние системы называется равно­весным.

Если между различными точками в системе существуют разности темпера­тур, давлений и других параметров, то она является неравновесной. В такой системе под действием гради­ентов параметров возникают потоки теп­лоты, вещества и другие, стремящиеся вернуть ее в состояние равновесия. Опыт показывает, что изолированная система с течением времени всегда приходит в со­стояние равновесия и никогда самопро­извольно выйти из него не может. В классической термодинамике рассмат­риваются только равновесные системы.
5.Термодинамические процессы: равновесные, неравновесные, обратные, прямые, обратимые, необратимые, замкнутые.

Изменение состояния термодинами­ческой системы во времени называется термодинамическим процессом. Так, при перемещении поршня в цилиндре объём, а с ним давление и температура находящегося внутри газа будут изменяться, будет совершаться процесс расширения или сжатия газа.

Термодинамический процесс называется равновесным, если все пара­метры системы при его протекании меня­ются достаточно медленно по сравнению с соответствующим процессом релакса­ции. В этом случае система фактически все время находится в состоянии равно­весия с окружающей средой, чем и опре­деляется название процесса.

Чтобы процесс был равновесным, скорость изменения параметров систе­мы должна удовлетворять соотно­шению



где А — параметр, наиболее быстро из­меняющийся в рассматриваемом процес­се; с_рел — скорость изменения этого па­раметра в релаксационном процессе; τрел — время релаксации.

Рассмотрим, например, процесс сжа­тия газа в цилиндре. Если время смеще­ния поршня от одного положения до дру­гого существенно превышает время ре­лаксации, то в процессе перемещения поршня давление и температура успеют выровняться по всему объему цилиндра.

Это выравнивание обеспечивается непре­рывным столкновением молекул, в ре­зультате чего подводимая от поршня к газу энергия достаточно быстро и рав­номерно распределяется между ними. Если последующие смещения поршня бу­дут происходить аналогичным образом, то состояние системы в каждый момент времени будет практически равновесным. Таким образом, равновесный процесс состоит из непрерывного ряда последо­вательных состояний равновесия, поэто­му в каждой его точке состояние термо­динамической системы можно описать уравнением состояния данного рабочего тела. Именно поэтому классическая термодинамика в своих исследованиях оперирует только равновесными процес­сами. Они являются удобной идеализа­цией реальных процессов, позволяющей во многих случаях существенно уп­ростить решение задачи. Такая идеали­зация вполне обоснована, так как условие (1.8) выполняется на практике до­статочно часто. Поскольку механические возмущения распространяются в газах со скоростью звука, процесс сжатия газа и цилиндре будет равновесным, если ско­рость перемещения поршня много мень­ше скорости звука.

Процессы, не удовлетворяющие усло­вию , протекают с нарушени­ем равновесия, т. е. являются неравновесными. Если, например, быстро увеличит температуру окружающей среды, то газ в цилиндре будет постепенно прогреваться через его стенки, релаксируя к состоянию равновесия, соответ­ствующему новым параметрам окружаю­щей среды. В процессе релаксации газ не находится в равновесии с окружаю­щей средой и его нельзя характеризовать уравнением состояния хотя бы потому, что в разных точках объема газа темпе­ратура имеет различные значения.

Последовательный ряд термодинамических процессов, в которых рабочее тело изменяет свое состояние и в результате возвращается в первоначальное состояние, называется круговым процессом, или циклом. Циклы могут быть обратимыми, состоящими из обратимых процессов, и необратимыми. Циклы подразделяются также на прямые и обратные. Прямыми называются циклы, в которых теплота преобразуется в работу, обратными — те, в которых теплота передается от более холодного тела к более нагретому.
Прямые циклы в диаграммах изображаются по часовой стрелке (по таким циклам работают все тепловые двигатели), обратные — против часовой стрелки (по таким циклам работают холодильные машины).
6. Понятие идеального газа.

Идеальным называется газ, у которого объемы молекул бесконечно малы и отсутствуют силы молекулярного взаимодействия. Молекулы идеального газа представляют собой материальные точки, взаимодействие между которыми ограничено молекулярными соударениями.

Любой реальный газ тем ближе к идеальному, чем ниже его давление и выше температура. Например, окружающий нас воздух можно считать идеальным газом. Понятие идеального газа и законы идеальных газов полезны в качестве предела законов реального газа.

На практике часто приходится иметь дело с газами при невысоких давлениях, поэтому расчеты различных термодинамических процессов с достаточной степенью точности можно проводить по уравнениям идеального газа.
7. Уравнение состояния идеального газа.

Из уравнений , и , следует, что .

Рассмотрим 1 кг газа. Учитывая, что в нем содержится N молекул и, следова­тельно, , получим: .

Постоянную величину Nk, отнесен­ную к 1 кг газа, обозначают буквой Rи называют газовойпостоян­ной. Поэтому

, или . (1.3)

Полученное соотношение представляет собой уравнение Клапейрона.

Умножив (1.3) на М, получим урав­нение состояния для произвольной массы газа М:

. (1.4)

Уравнению Клапейрона можно при­дать универсальную форму, если отнести газовую постоянную к 1 кмолю газа, т. е. к количеству газа, масса которого в килограммах численно равна молеку­лярной массе μ. Положив в (1.4) М=μ и V=V μ, получим для одного моля урав­нение Клапейрона — Менделеева:

.

Здесь — объем киломоля газа, а — универсальная газовая постоянная.

В соответствии с законом Авогадро (1811г.) объем 1 кмоля, одинаковый в одних и тех же условиях для всех иде­альных газов, при нормальных физических условиях равен 22,4136 м³, поэтому



Газовая постоянная 1 кг газа составляет .
8. Газовые смеси. Закон Дальтона.

В инженерной прак­тике часто приходится иметь дело с газо­образными веществами, близкими по свойствам к идеальным газам и пред­ставляющими собой механическую смесь отдельных компонентов различных газов, химически не реагирующих между собой. Это так называемые газовые сме­си. В качестве примера можно назвать продукты сгорания топлива в двигателях внутреннего сгорания, топках печей и па­ровых котлов, влажный воздух в сушиль­ных установках и т. п.

Основным законом, определяющим поведение газовой смеси, является закон Дальтона: полное давление смеси иде­альных газов равно сумме парциальных давлений всех входящих в нее компо­нентов: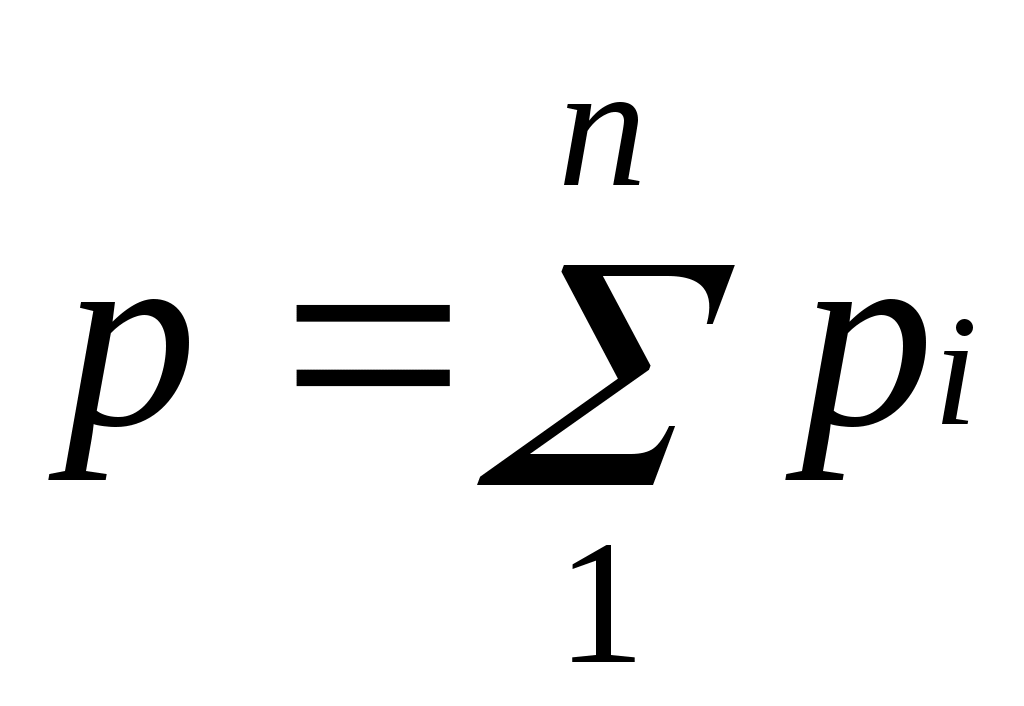



Парциальноедавление pi — давление, которое имел бы газ, если бы он один при той же температуре занимал весь объем смеси.
9. Способы задания состава газовых смесей.

Состав га­зовой смеси может быть задан массовы­ми, объемными или мольными долями.

Массовой долей называется отношение массы отдельного компонента Мi, к массе смеси М:

.

Очевидно, что 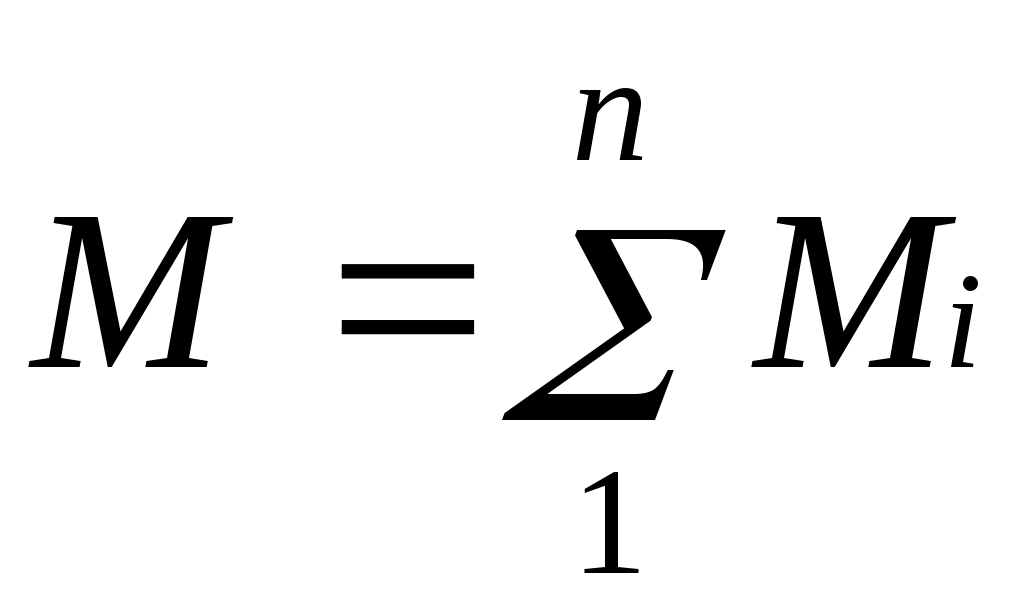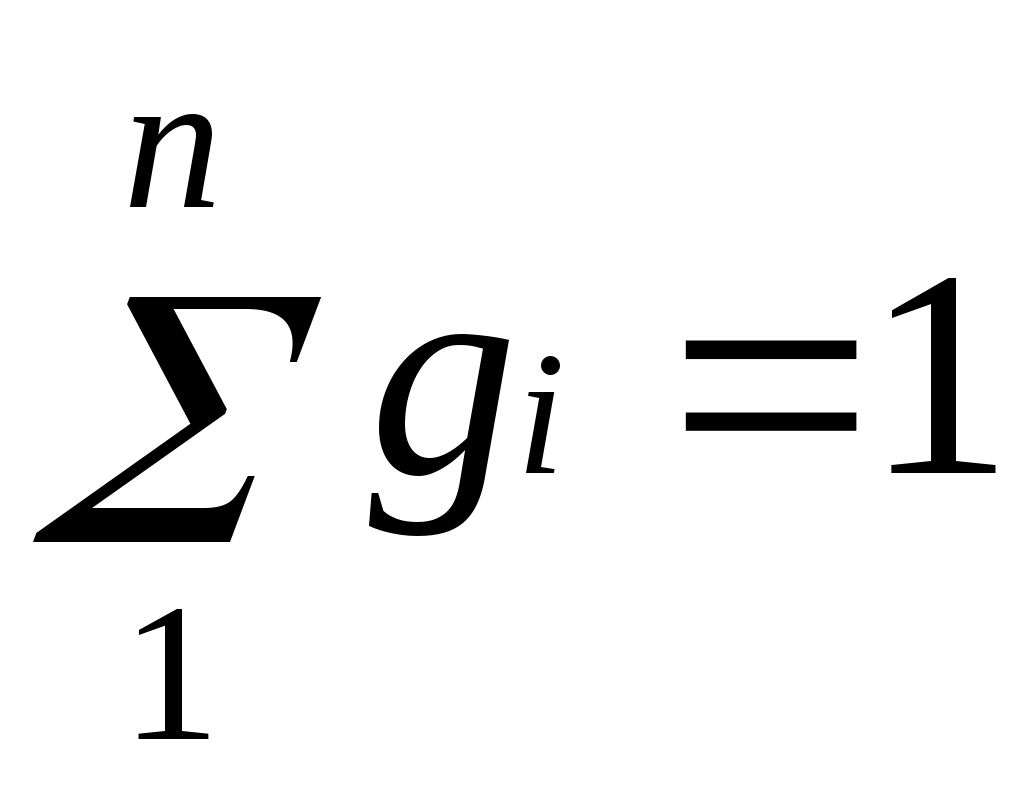и .

Массовые доли часто задаются в процентах. Например, для сухого воздуха ; .

Объемная доля представляет собой отношение приведенного объема газа V, к полному объему смеси V: .

Приведенным называется объем, который занимал бы компонент газа, ес­ли бы его давление и температура равня­лись давлению и температуре смеси.

Для вычисления приведенного объема запишем два уравнения состоя­ния i-го компонента:

; (2.1)

.

Первое уравнение относится к состоянию компонента газа в Смеси, когда он имеет парциальное давление pi и занимает пол­ный объем смеси, а второе уравнение — к приведенному состоянию, когда давле­ние и температура компонента равны, как и для смеси, р и Т. Из уравнений следует, что

. (2.2)

Просуммировав соотношение (2.2) для всех компонентов смеси, получим с учетом закона Дальтона 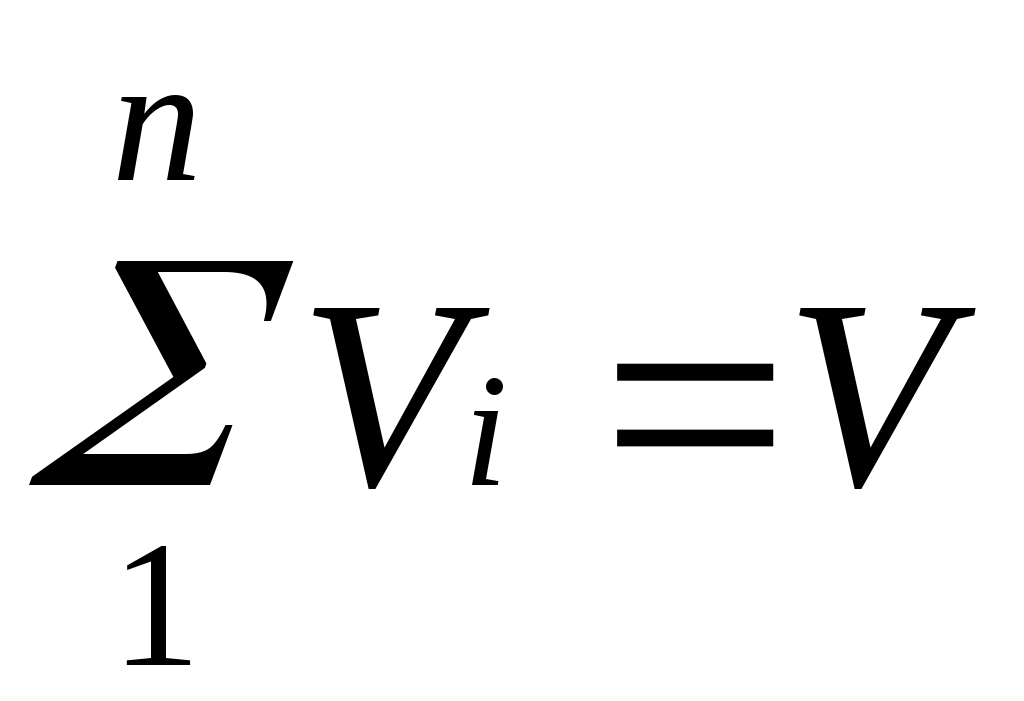,откуда . Объемные доли также часто задаются в процентах. Для воз­духа , .

Иногда бывает удобнее задать со­став смеси мольными долями. Моль­ной долей называется отношение количества молей Ni рассматриваемого компонента к общему количеству молей смеси N.

Пусть газовая смесь состоит из N1 молей первого компонента, N2 молей вто­рого компонента и т. д. Число молей смеси , а мольная доля компонента будет равна .

В соответствии с законом Авогадро объемы моля любого газа при одинако­вых р и Т, в частности при температуре и давлении смеси, в идеально газовом состоянии одинаковы. Поэтому приве­денный объем любого компонента может быть вычислен как произведение объема моля на число молей этого компо­нента, т. е. а объем смеси — по формуле . Тогда , и, следовательно, задание смесильных газов мольными долями равно заданию ее объемными долями.

10. Теплоемкость, определение, виды, уравнения связи.

Отношение количества теплоты , полученного телом при бесконечно малом изменении его состояния, к связанному с этим изменению температуры тела , называется теплоемкостью тела в данном процессе:

.

Обычно теплоемкость относят к еди­нице количества вещества и в зависимо­сти от выбранной единицы различают:

удельную массовую теп­лоемкость c , отнесенную к 1 кг газа,

Дж/(кг·К);

удельнуюобъемную теп­лоемкость c´, отнесенную к количеству газа, содержащегося в 1 м³ объема при нормальных физических условиях, Дж/(м³·К);

удельнуюмольнуютепло­емкость , отнесенную к одному киломолю, Дж/(кмоль·К).

Зависимость между удельными теплоемкостями устанавливается очевидны­ми соотношениями: ;

Здесь — плотность газа при нормаль­ных условиях.

Изменение температуры тела при од­ном и том же количестве сообщаемой теплоты зависит от характера происходя­щего при этом процесса, поэтому тепло­емкость является функцией процесса. Это означает, что одно и то же рабочее тело в зависимости от процесса требует для своего нагревания на 1 К различного ко­личества теплоты. Численно величина с изменяется в пределах от +∞ до -∞.

В термодинамических расчетах боль­шое значение имеют:

теплоемкость при посто­янном давлении

,

равная отношению количества теплоты , сообщенной телу в процессе при по­стоянном давлении, к изменению температуры тела dT

теплоемкость при посто­янном объеме

, (1.5)

равная отношению количества теплоты , подведенной к телу в процессе при постоянном объеме, к изменению темпе­ратуры тела .

В соответствии с первым законом термодинамики для закрытых систем, в которых протекают равновесные про­цессы , и

.

Для изохорного процесса (v=const) это уравнение принимает вид , и, учитывая (1.5), по­лучаем, что

,

т. е. теплоемкость тела при постоянном объеме равна частной производной от его внутренней энергии по температуре и характеризует темп роста внутренней энергии в изохорном процессе с увеличе­нием температуры.

Для идеального газа

Для изобарного процесса () из уравнения (2.16) и (2.14) получаем



или



Это уравнение показывает связь между теплоемкостями с_ри сv. Для иде­ального газа оно значительно упрощает­ся. Действительно, внутренняя энергия идеального газа определяется только его температурой и не зависит от объема, поэтому и, кроме того, из уравнения состояния следует , откуда

.

Это соотношение называется уравнением Майера и является одним из основных в технической термодинамике идеальных газов.

В процессе v=const теплота, сооб­щаемая газу, идет лишь на изменение его внутренней энергии, тогда как в про­цессе р = const теплота расходуется и на увеличение внутренней энергии и на со­вершение работы против внешних сил. Поэтому с_рбольше сvна величину этой работы.

Для реальных газов , по­скольку при их расширении (при p=const) совершается работа не только против внешних сил, но и против сил притяжения, действующих между моле­кулами, что вызывает дополнительный расход теплоты.

Числовое значение теплоемкости идеаль­ного газа позволяет найти классическая тео­рия теплоемкости, основанная на теореме о равномерном распределении энергии по сте­пеням свободы молекул. Согласно этой теоре­ме внутренняя энергия идеального газа прямо пропорциональна числу степеней свободы мо­лекул и энергии kТ/2, приходящейся на одну степень свободы. Для 1 моля газа

,

где Nо — число Авогадро; i— число степеней свободы (число независимых координат, которые нужно задать для того, чтобы полно­стью определить положение молекулы в про­странстве) .

Поскольку для идеального газа , то мольные теплоемкости одно-, двух- и многоатомных газов равны со­ответственно:

; ; .

.

Теплоемкость реального газа зависит от давления, правда, очень слабо.

Поскольку теплоемкость реального газа зависит от температуры, в термоди­намике различают истинную и среднюю теплоемкости.

Среднейтеплоемкостью с_ср данного процесса в интер­вале температур от t1 доt2 называется отношение количества тепло­ты, сообщаемой газу, к разности конеч­ной и начальной температур:



Выражение

*

определяет теплоемкость при данной температуре или так называемую истиннуютеплоемкость. Из * следует, что



поэтому

.

Для практических расчетов теплоем­кости всех веществ сводят в таблицы, причем с целью сокращения объема таб­лиц средние теплоемкости приводят в них для интервала температур от 0 до t.
11. Внутренняя энергия.

Внутренняя энергия системы включа­ет в себя:

кинетическую энергию поступатель­ного, вращательного и колебательного движения частиц;

потенциальную энергию взаимодей­ствия частиц;

энергию электронных оболочек атомов;

внутриядерную энергию.

В большинстве теплоэнергетических процессов две последние составляющие остаются неизменными. Поэтому в даль­нейшем под внутренней энер­гией будем понимать энергию хаотиче­ского движения молекул и атомов, вклю­чающую энергию поступательного, вра­щательного и колебательного движений как молекулярного, так и внутримолекулярного, а также потенциальную энергию сил взаимодействия между молекулами.

Кинетическая энергия молекул явля­ется функцией температуры, значение потенциальной энергии зависит от сред­него расстояния между молекулами и, следовательно, от занимаемого газом объема V, т. е. является функцией V. По­этому внутренняя энергия U есть функ­ция состояния тела.

Для сложной системы она определя­ется суммой энергий отдельных частей, т. е. обладает свойством аддитивности. Величина и=U/М, называемая удельнойвнутренней энер­гией (Дж/кг), представляет собой внутреннюю энергию единицы массы ве­щества.

В дальнейшем для краткости будем называть величину и просто внутренней энергией. Поскольку внутренняя энергия есть функция состояния тела, то она мо­жет быть представлена в виде функции двух любых независимых параметров, определяющих это состояние:

; ; .

Ее изменение в термодинамическом процессе не зависит от характера процесса и определяется только началь­ным и конечным состояниями тела:

;

— значение внутренней энергии в начальном состоянии, а — в конечном. Математически это означает, что бесконечно малое измене­ние внутренней энергии duесть полный дифференциал и; если выразить внутрен­нюю энергию в виде функции удельного объема и температуры, то



Внутренняя энергия идеального газа, в котором отсутствуют силы взаимодей­ствия между молекулами, не зависит от объема газа или давления , а определяется только его температурой, поэтому производная от внутренней энергии идеального газа по температуре есть полная производная:



Для задач технической термодинами­ки важно не абсолютное значение внут­ренней энергии, а ее изменение в различ­ных термодинамических процессах. По­этому начало отсчета внутренней энер­гии может быть выбрано произвольно. Например, в соответствии с международ­ным соглашением для воды за нуль при­нимается значение внутренней энергии при температуре 0,01 °С и давление 610,8 Па, а для идеальных газов — при 0 °С вне зависимости от давления.
12. Энтальпия.

В термодинамике важную роль игра­ет сумма внутренней энергии системы Uи произведения давления системы р на ее объем V, называемая энтальпией и обозначаемая Н: