|
|
Билеты теплофизика. билеты по теплофизике. Техническая термодинамика цели и задачи. Основные понятия и определения рабочее тело, термодинамическая система (тдс), виды тдс
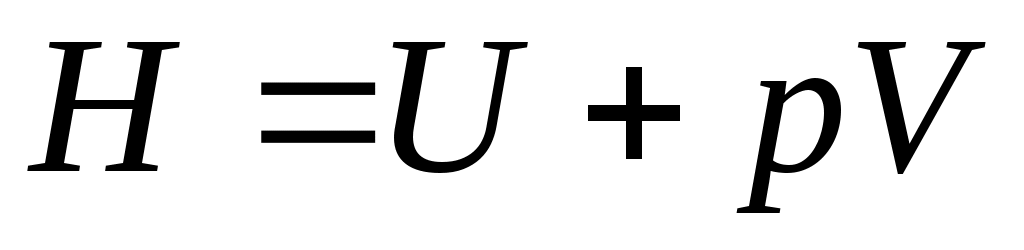 . .
Так как входящие в нее величины являются функциями состояния, то и сама энтальпия является функцией состояния. Так же как внутренняя энергия, работа и теплота, она измеряется в джоулях (Дж).
Энтальпия обладает свойством аддитивности. Величина
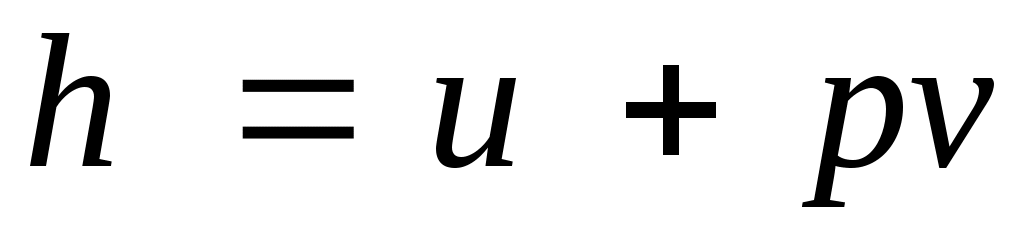 , ,
называемая удельной энтальпией (h = H/M), представляет собой энтальпию системы, содержащей 1 кг вещества, и измеряется в Дж/кг.
Поскольку энтальпия есть функция состояния, то она может быть представлена в виде функции двух любых параметров состояния:
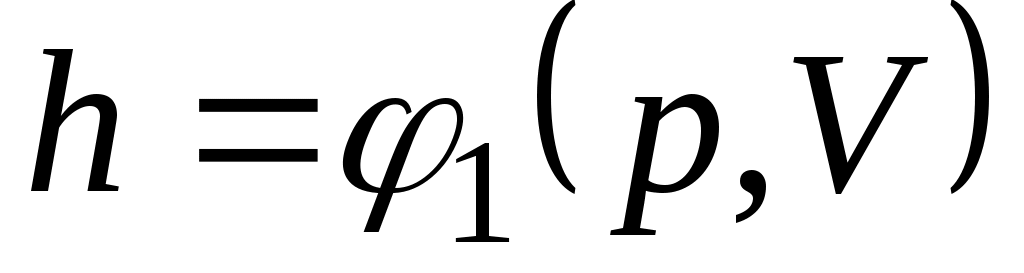 ; ; 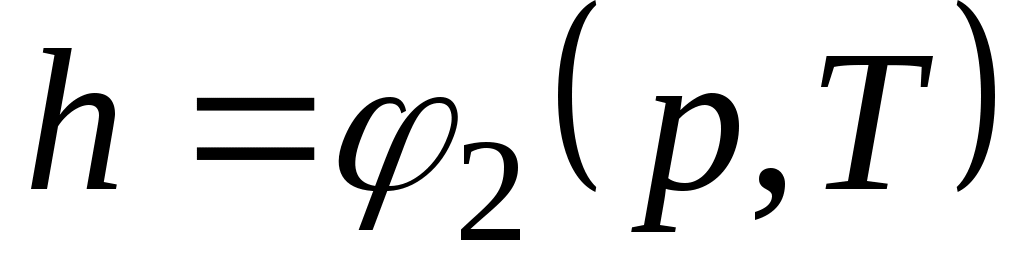 ; ; 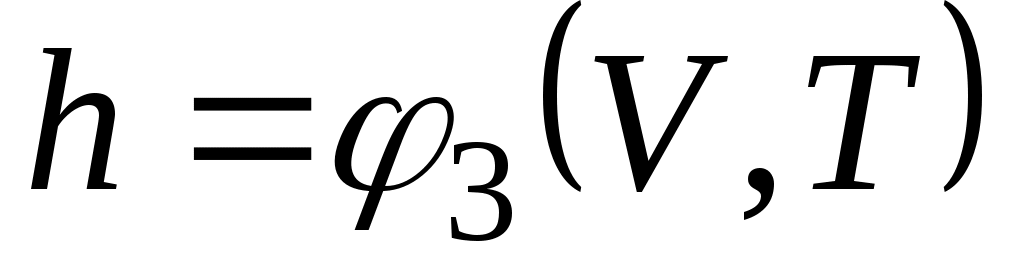 , ,
а величина dhявляется полным дифференциалом.
Изменение энтальпии в любом процессе определяется только начальным и конечным состояниями тела и не зависит от характера процесса.
Физический смысл энтальпии выясним на следующем примере. Рассмотрим расширенную систему, включающую газ в цилиндре и поршень с грузом общим весом G .
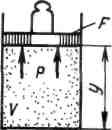
Энергия этой системы складывается из внутренней энергии газа и потенциальной энергии поршня с грузом в поле внешних сил: . В условиях равновесия (G = pF) эту функцию можно выразить через параметры газа: . В условиях равновесия (G = pF) эту функцию можно выразить через параметры газа: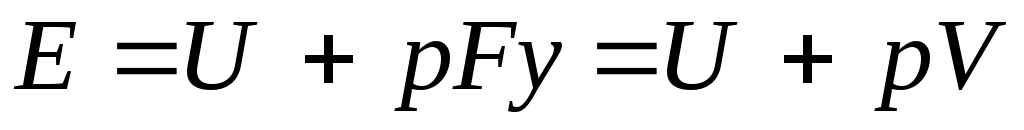 . Получаем, что . Получаем, что 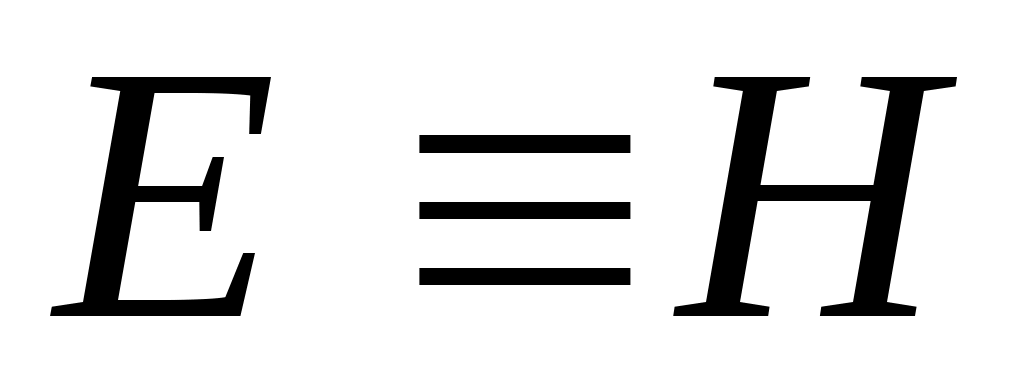 , т.е. энтальпию можно трактовать как энергию расширенной системы. , т.е. энтальпию можно трактовать как энергию расширенной системы.
Уравнение  в случае, когда единственным видом работы является работа расширения, с учетом очевидного соотношения в случае, когда единственным видом работы является работа расширения, с учетом очевидного соотношения  может быть записано в виде может быть записано в виде 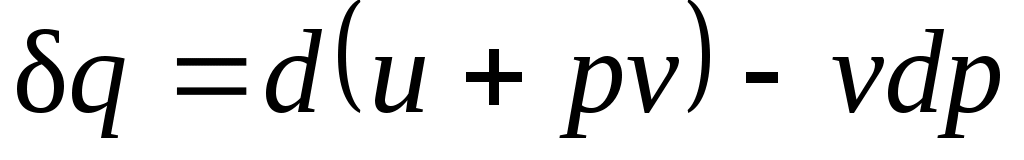 , или , или
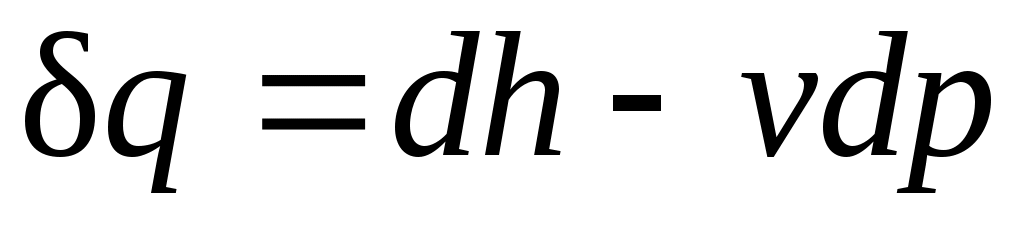 . .
Из этого соотношения следует, что если давление системы сохраняется неизменным, т. е. осуществляется изобарный процесс (dp=0), то
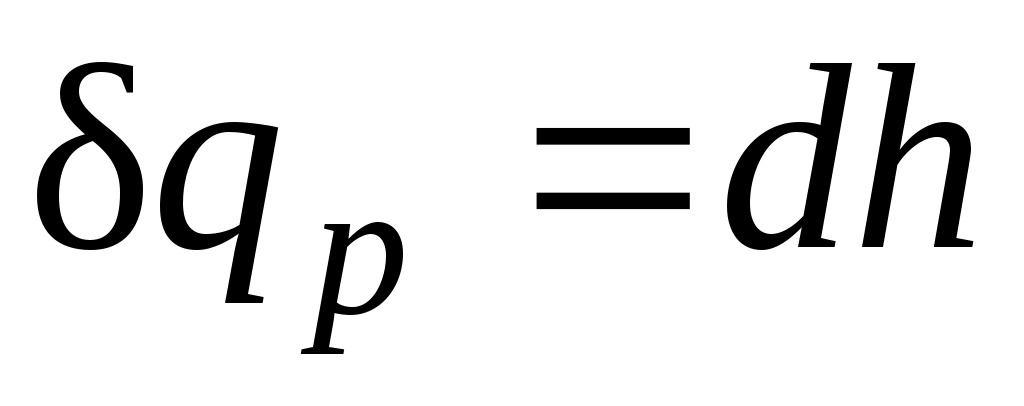 и и  . .
т. е. теплота, подведенная к системе при постоянном давлении, идет только на изменение энтальпии данной системы.
Это выражение очень часто используется в расчетах, так как огромное количество процессов подвода теплоты в теплоэнергетике (в паровых котлах, камерах сгорания газовых турбин и реактивных двигателей, теплообменных аппаратах), а также целый ряд процессов химической технологии и многих других осуществляется при постоянном давлении. Кстати, по этой причине в таблицах термодинамических свойств обычно приводятся значения энтальпии, а не внутренней энергии.
Для идеального газа с учетом получим
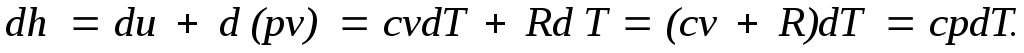
Так как между энтальпией и внутренней энергией существует связь 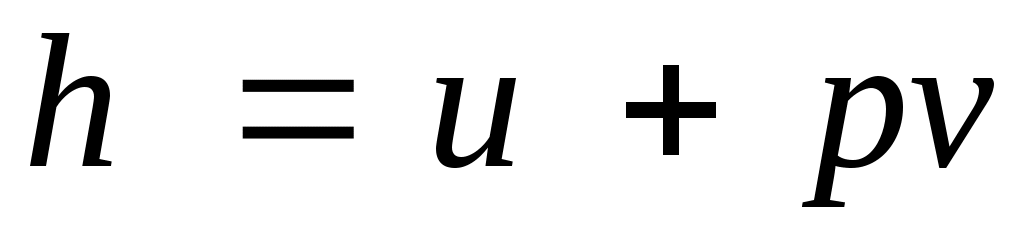 , выбор начала отсчета одной из них не произволен: в точке, принятой за начало отсчета внутренней энергии, h = pv. , выбор начала отсчета одной из них не произволен: в точке, принятой за начало отсчета внутренней энергии, h = pv.
Например, для воды при t=0.01ºC и р =610,8 Па, u = 0, a
h = pv = 0,611 Дж/кг.
При расчетах практический интерес представляет изменение энтальпии в конечном процессе: 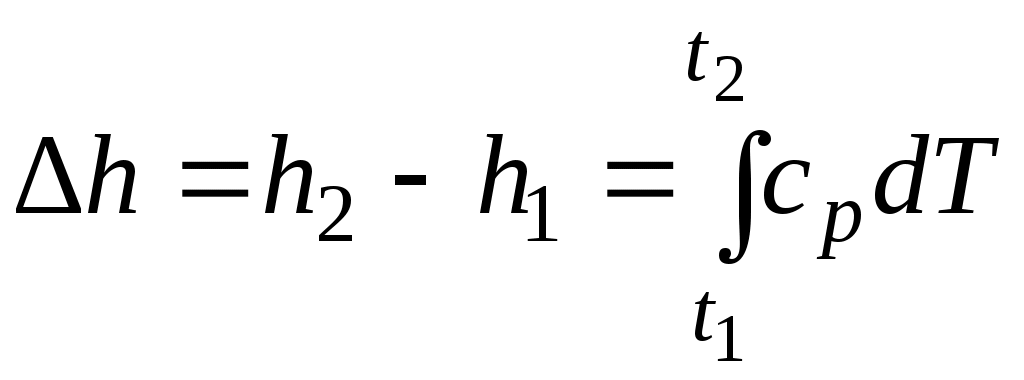 . .
13. Теплота.
Помимо макрофизической формы передачи энергии — работы существует также и микрофизическая, т. е. осуществляемая на молекулярном уровне форма обмена энергией между системой и окружающей средой. В этом случае энергия может быть передана системе без совершения работы. Мерой количества энергии, переданной микрофизическим путем, служит теплота.
Теплота может передаваться либо при непосредственном контакте между телами (теплопроводностью, конвекцией), либо на расстоянии (излучением), причем во всех случаях этот процесс возможен только при наличии разности температур между телами.
Как будет показано ниже, элементарное количество теплоты  , так же как и L, не является полным дифференциалом в отличие от дифференциала внутренней энергии dU. За этой математической символикой скрыт глубокий физический смысл различия понятий внутренней энергии, теплоты и работы. , так же как и L, не является полным дифференциалом в отличие от дифференциала внутренней энергии dU. За этой математической символикой скрыт глубокий физический смысл различия понятий внутренней энергии, теплоты и работы.
Внутренняя энергия — это свойство самой системы, она характеризует состояние системы. Теплота и работа — это энергетические характеристики процессов механического и теплового взаимодействий системы с окружающей средой. Они характеризуют те количества энергии, которые переданы системе или отданы ею через ее границы в определенном процессе.
14. Работа.
Работа в термодинамике, так же как и в механике, определяется произведением действующей на рабочее тело силы на путь ее действия.
Р ассмотрим газ массой М и объемом V, заключенный в эластичную оболочку с поверхностью F. ассмотрим газ массой М и объемом V, заключенный в эластичную оболочку с поверхностью F.
Если газу сообщить некоторое количество теплоты, то он будет расширяться, совершая при этом работу против внешнего давления р, оказываемого на него средой. Газ действует на каждый элемент оболочки dFс силой, равной pdFи, перемещая ее по нормали к поверхности на расстояние dn, совершает элементарную работу pdFdn. Общую работу, совершенную в течение бесконечно малого процесса, получим, интегрируя данное выражение по всей поверхности Fоболочки: 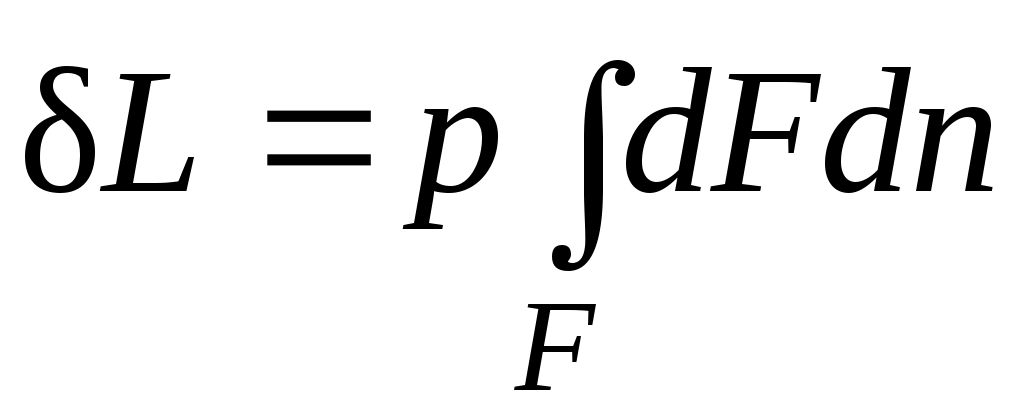 . .
Из рисунка видно, что изменение объема dVвыражается в виде интеграла по поверхности: 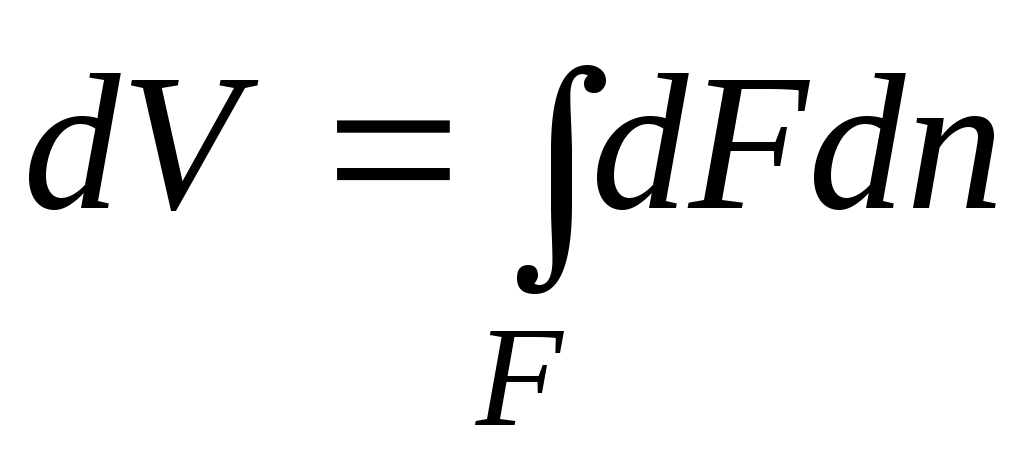 , следовательно , следовательно
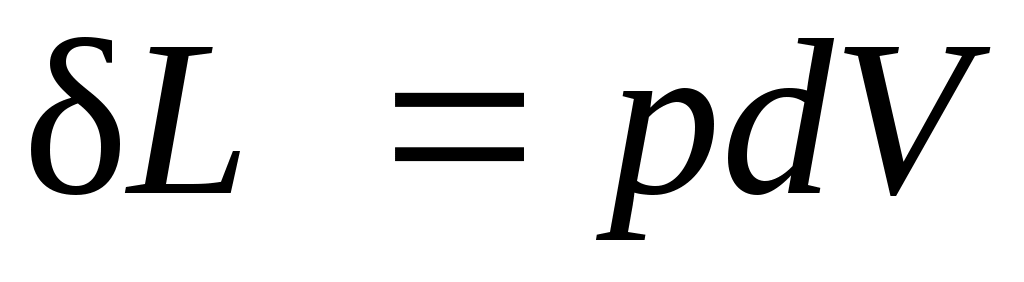 . (3.1) . (3.1)
При конечном изменении объема работа против сил внешнего давления, называемая работойрасширения, равна
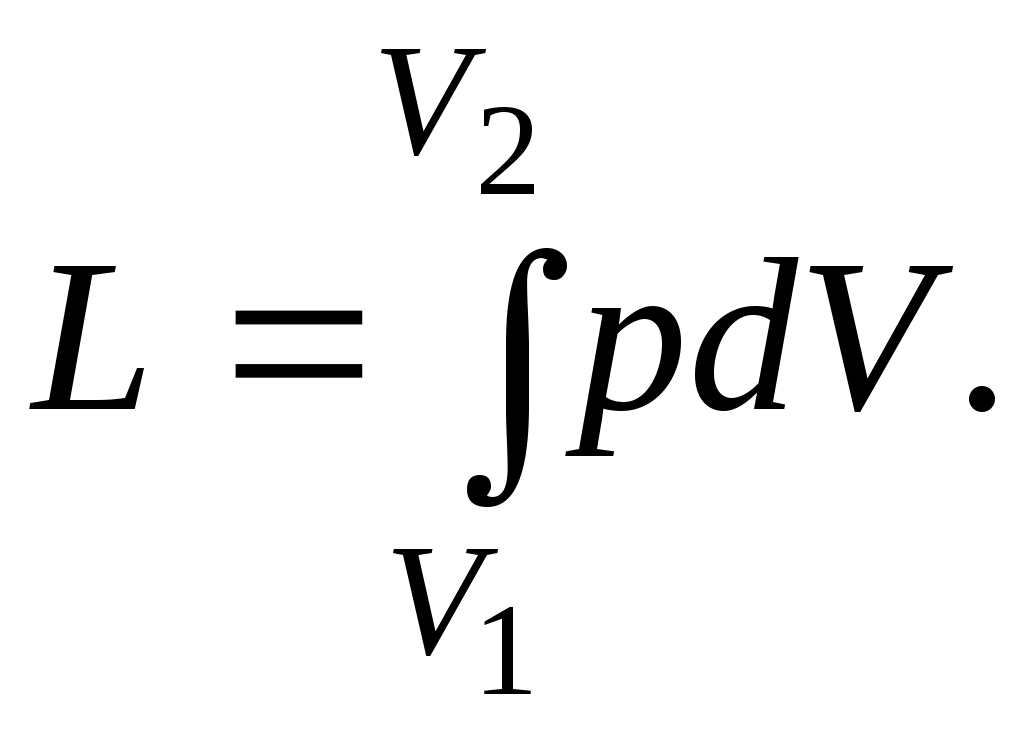
Из (3.1) следует, что 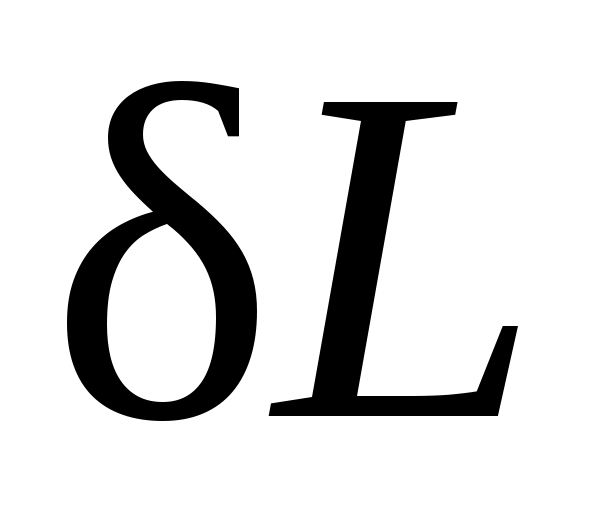 и dVвсегда имеют одинаковые знаки: и dVвсегда имеют одинаковые знаки:
если dV>0, то и 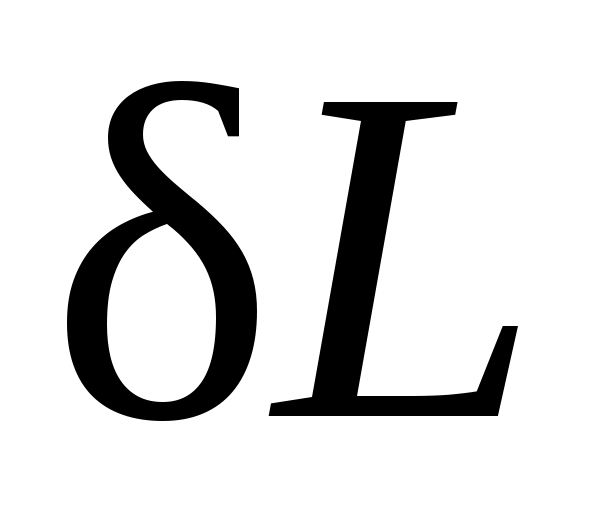 >0, т. е. при расширении работа тела положительна, при этом тело само совершает работу; >0, т. е. при расширении работа тела положительна, при этом тело само совершает работу;
если же dV<0, то и 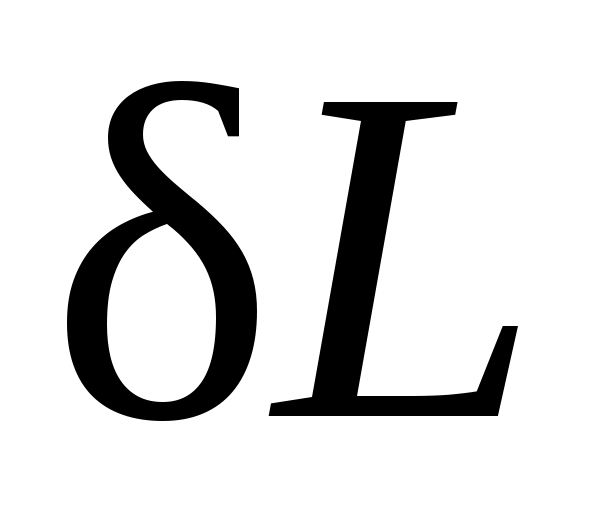 <0, т. е. при сжатии работа тела отрицательна: это означает, что не тело совершает работу, а на его сжатие затрачивается работа извне. Единицей измерения работы в СИ является джоуль (Дж). <0, т. е. при сжатии работа тела отрицательна: это означает, что не тело совершает работу, а на его сжатие затрачивается работа извне. Единицей измерения работы в СИ является джоуль (Дж).
Отнеся работу расширения к 1 кг массы рабочего тела, получим
l = L/M; 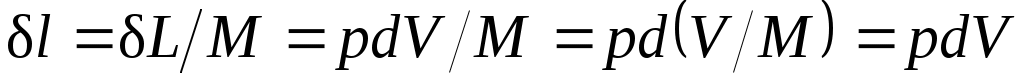 . .
Величина , представляющая собой удельную работу, совершаемую системой, содержащей 1 кг газа, равна
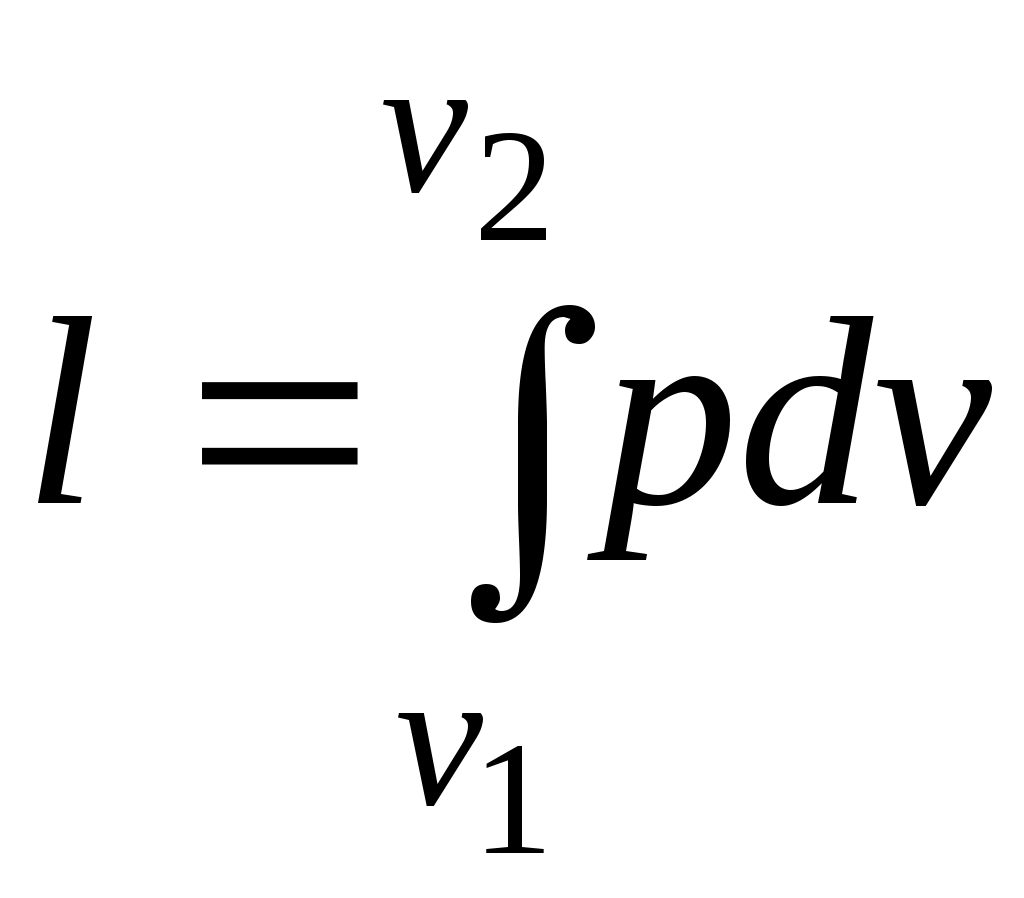 . (3.2) . (3.2)
Поскольку в общем случае р — величина переменная, то интегрирование возможно лишь тогда, когда известен закон изменения давления р = р(v).
Формулы (3.1) — (3.2) справедливы только для равновесных процессов, при которых давление рабочего тела равно давлению окружающей среды.
В термодинамике для исследования равновесных процессов широко используют р,v– диаграмму, в которой осью абсцисс служит удельный объем, а осью ординат — давление. Поскольку состояние термодинамической системы определяется двумя параметрами, то на р,v– диаграмме оно изображается точкой. На рисунке точка 1 соответствует начальному состоянию системы, точка 2 — конечному, а линия 12 — процессу расширения рабочего тела от v1 до v2. При бесконечно малом изменении объема площадь заштрихованной вертикальной полоски равна 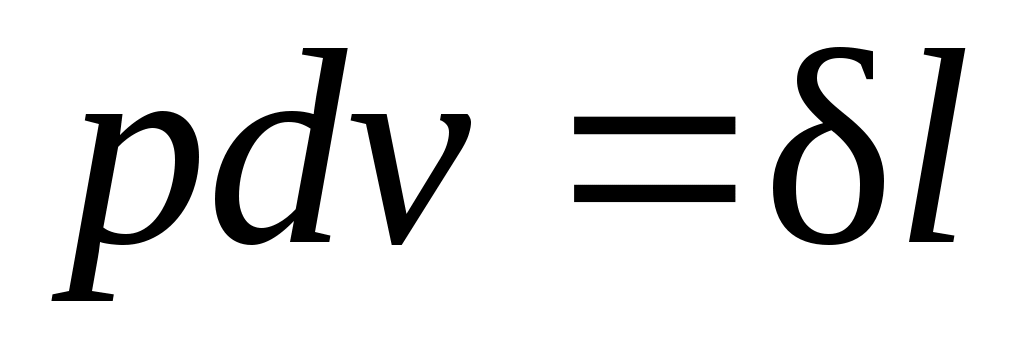 ; следовательно, работа процесса 12 изображается площадью, ограниченной кривой процесса, осью абсцисс и крайними ординатами. ; следовательно, работа процесса 12 изображается площадью, ограниченной кривой процесса, осью абсцисс и крайними ординатами.
Таким образом, работа изменения объема эквивалентна площади под кривой процесса в диаграмме р, v (рисунок 3.1).
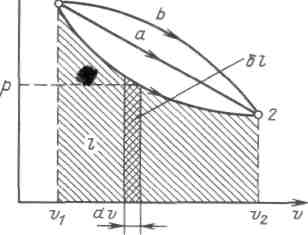
Рисунок 3.1 - Графическое изображение работы в р, v – координатах
Каждому пути перехода системы из состояния / в состояние 2 (например, 12, 1а2 или 1b2) соответствует своя работа расширения.Следовательно, работа зависит от характера термодинамического процесса, а не является функцией только исходного и конечного состояний системы. С другой стороны,  зависит от пути интегрирования и, следовательно, элементарная работа зависит от пути интегрирования и, следовательно, элементарная работа 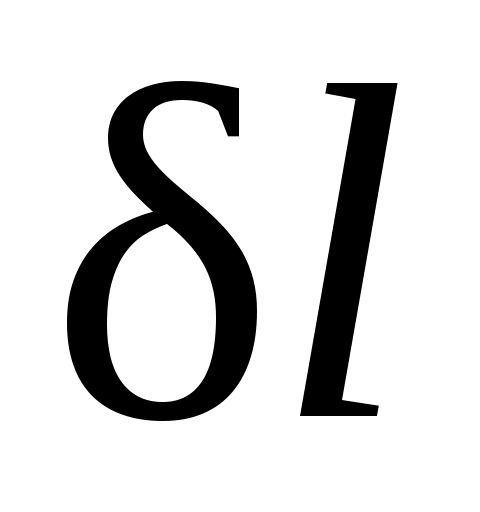 не является полным дифференциалом. не является полным дифференциалом.
Работа всегда связана с перемещением макроскопических тел в пространстве, например перемещением поршня, деформацией оболочки, поэтому она характеризует упорядоченную (макрофизическую) форму передачи энергии от одного тела к другому и является мерой переданной энергии. Поскольку величина 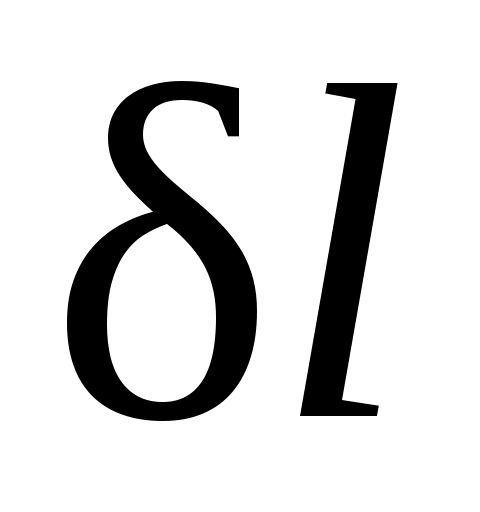 пропорциональна увеличению объема, то в качестве рабочих тел, предназначенных для преобразования тепловой энергии в механическую, целесообразно выбирать такие, которые обладают способностью значительно увеличивать свой объем. Этим качеством обладают газы и пары жидкостей. Поэтому, например, на тепловых электрических станциях рабочим телом служат пары воды, а в двигателях внутреннего сгорания — газообразные продукты сгорания того или иного топлива. пропорциональна увеличению объема, то в качестве рабочих тел, предназначенных для преобразования тепловой энергии в механическую, целесообразно выбирать такие, которые обладают способностью значительно увеличивать свой объем. Этим качеством обладают газы и пары жидкостей. Поэтому, например, на тепловых электрических станциях рабочим телом служат пары воды, а в двигателях внутреннего сгорания — газообразные продукты сгорания того или иного топлива.
15. Первый закон термодинамики. Аналитическое выражение, частные случаи.
Первый закон термодинамики представляет собой частный случай всеобщего закона сохранения и превращения энергии применительно к тепловым явлениям.
Пусть некоторому рабочему телу с объемом Vи массой М, имеющему температуру Т и давление р, сообщается извне бесконечно малое количество теплоты  . В результате подвода теплоты тело нагревается на dTи увеличивается в объеме на dV. . В результате подвода теплоты тело нагревается на dTи увеличивается в объеме на dV.
Повышение температуры тела свидетельствует об увеличении кинетической энергии его частиц. Увеличение объема тела приводит к изменению потенциальной энергии частиц. В результате внутренняя энергия тела увеличивается на dU. Поскольку рабочее тело окружено средой, которая оказывает на него давление, то при расширении оно производит механическую работу  против сил внешнего давления. Так как никаких других изменений в системе не происходит, то по закону сохранения энергии против сил внешнего давления. Так как никаких других изменений в системе не происходит, то по закону сохранения энергии
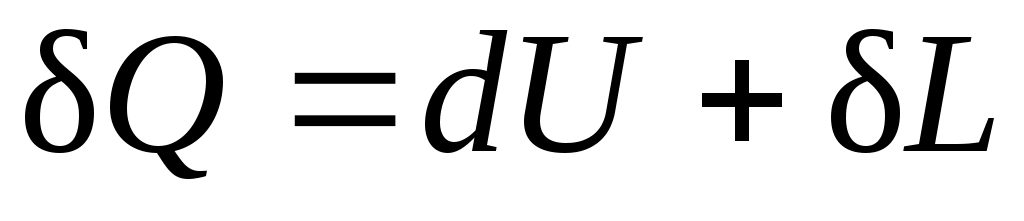 (2.8) (2.8)
т. е. теплота, сообщаемая системе, идет на приращение ее внутренней энергии и на совершение внешней работы.
Полученное уравнение является математическим выражением первого закона термодинамики. Каждый из трех членов этого соотношения может быть положительным, отрицательным или равным нулю. Рассмотрим некоторые частные случаи.
1.  — теплообмен системы с окружающей средой отсутствует, т. е. теплота к системе не подводится и от нее не отводится. Процесс без теплообмена называется адиабатным. Для него уравнение (2.8) принимает вид: — теплообмен системы с окружающей средой отсутствует, т. е. теплота к системе не подводится и от нее не отводится. Процесс без теплообмена называется адиабатным. Для него уравнение (2.8) принимает вид:
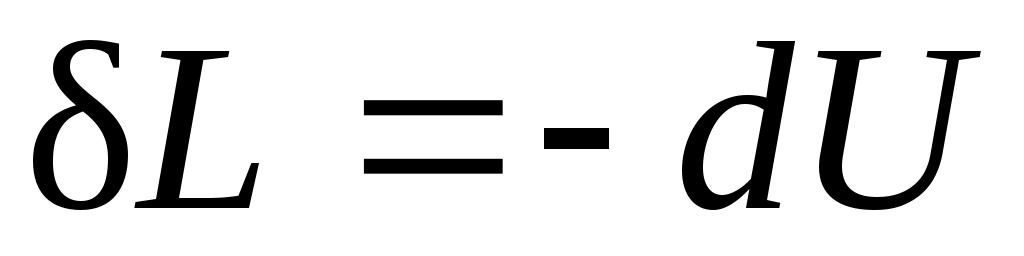 . .
Следовательно, работа расширения, совершаемая системой в адиабатном процессе, равна уменьшению внутренней энергии данной системы. При адиабатном сжатии рабочего тела затрачиваемая извне работа целиком идет на увеличение внутренней энергии системы.
2.  — при этом объем тела не изменяется, dV=0 . Такой процесс называется изохорным, для него — при этом объем тела не изменяется, dV=0 . Такой процесс называется изохорным, для него
 , ,
т. е. количество теплоты, подведенное к системе при постоянном объеме, равно увеличению внутренней энергии данной системы.
dU=0 – внутренняя энергия системы не изменяется и
 , ,
т.е. сообщаемая системе теплота превращается в эквивалентную ей внешнюю работу.
Для системы, содержащей 1 кг рабочего тела
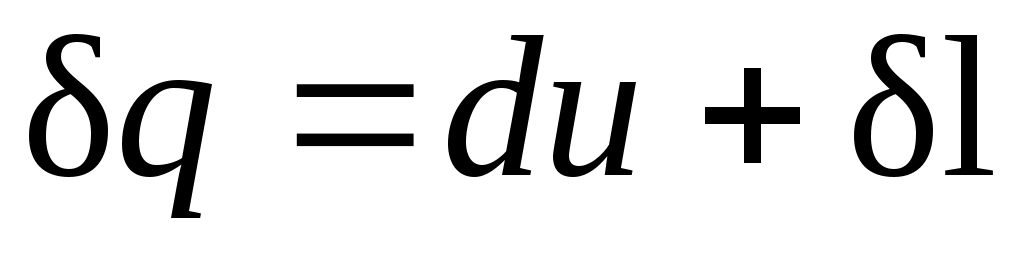 . (2.9) . (2.9)
Проинтегрировав уравнения (2.8) и (2.9) для некоторого процесса, получим выражение первого закона термодинамики в интегральной форме:
 ; ; 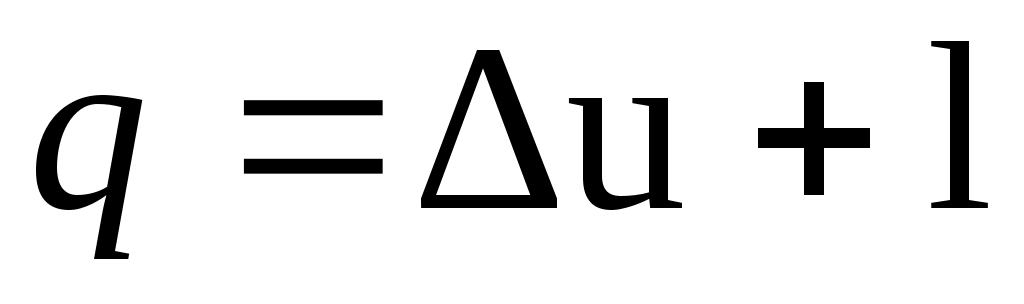 . .
16 Энтропия.
Как уже указывалось, величина  не является полным дифференциалом. Действительно, для того чтобы проинтегрировать правую часть этого выражения, нужно знать зависимость р от v, т. е. процесс, который совершает газ. не является полным дифференциалом. Действительно, для того чтобы проинтегрировать правую часть этого выражения, нужно знать зависимость р от v, т. е. процесс, который совершает газ.
В математике доказывается, что дифференциальный двучлен всегда можно превратить в полный дифференциал путем умножения (или деления) на интегрирующий множитель (или делитель). Таким интегрирующим делителем для элементарного количества теплоты qявляется абсолютная температура Т.
Покажем это на примере изменения параметров идеального газа в равновесных процессах:
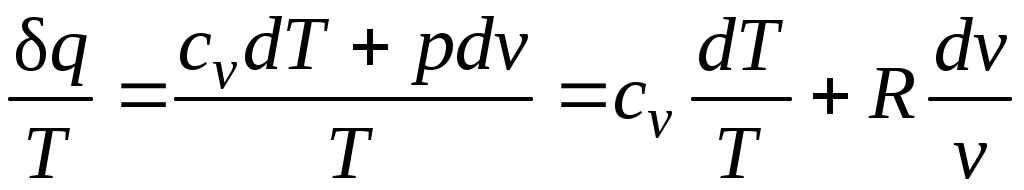 . (3.3) . (3.3)
Выражение  при равновесном изменении состояния газа есть полный дифференциал некоторой функции состояния. Она называется энтропией, обозначается для 1 кг газа через s и измеряется в Дж/(кгК). Для произвольного количества газа энтропия, обозначаемая через S, равна S=Msи измеряется в Дж/К. при равновесном изменении состояния газа есть полный дифференциал некоторой функции состояния. Она называется энтропией, обозначается для 1 кг газа через s и измеряется в Дж/(кгК). Для произвольного количества газа энтропия, обозначаемая через S, равна S=Msи измеряется в Дж/К.
Таким образом, аналитически энтропия определяется следующим образом:
 . (3.4) . (3.4)
Формула (3.4) справедлива как для идеальных газов, так и для реальных тел. Подобно любой другой функции состояния энтропия может быть представлена в виде функции любых двух параметров состояния:
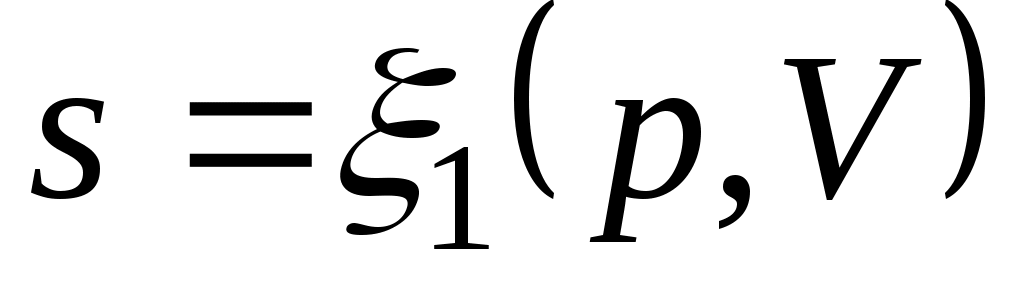 ; ; 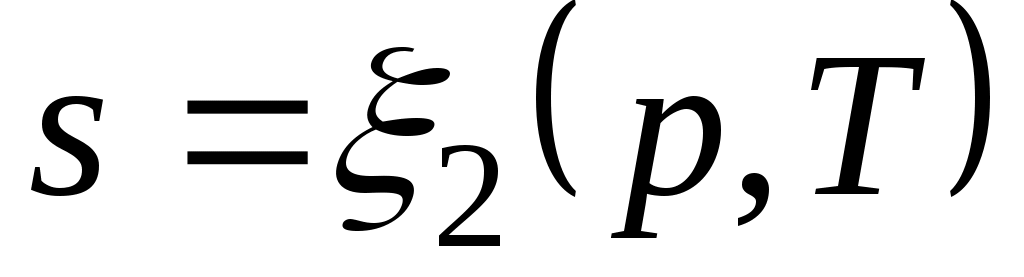 ; ; 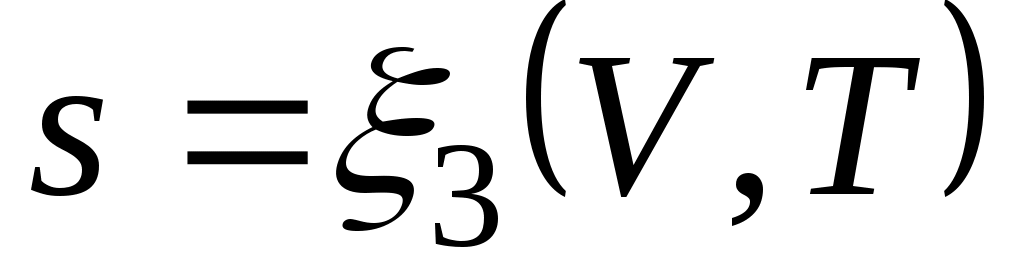 . .
Значение энтропии для заданного состояния определяется интегрированием уравнения (3.4):
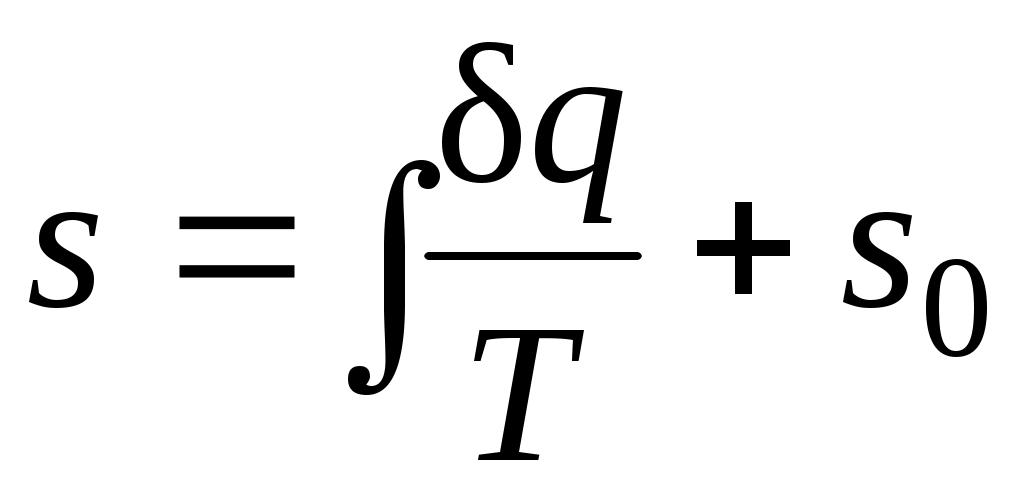
где  — константа интегрирования. — константа интегрирования.
При температурах, близких к абсолютному нулю, все известные вещества находятся в конденсированном состоянии. В. Нернст (1906 г.) экспериментально установил, а М. Планк (1912 г.) окончательно сформулировал следующий принцип: при температуре , стремящейся к абсолютному нулю, энтропия вещества, находящегося в конденсированном состоянии с упорядоченной кристаллической структурой, стремится к нулю, т. е. s0 = 0 при Т = 0 К. Этот закон называют третьимзаконом термодинамики или тепловой теоремой Нернста. Он позволяет рассчитать абсолютное значение энтропии в отличие от внутренней энергии и энтальпии, которые всегда отсчитываются от произвольного уровня.
Однако в технической термодинамике обычно используется не абсолютное значение энтропии, а ее изменение в каком-либо процессе:
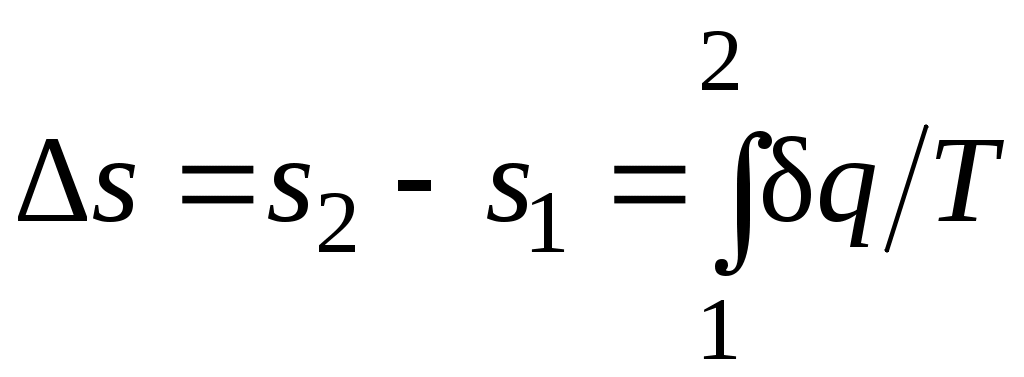 , ,
поэтому энтропию тоже часто отсчитывают от произвольно выбранного уровня.
Получим формулы, позволяющие вычислить изменение энтропии идеального газа. Для этого проинтегрируем уравнение (3.3), положив для простоты cv= const:
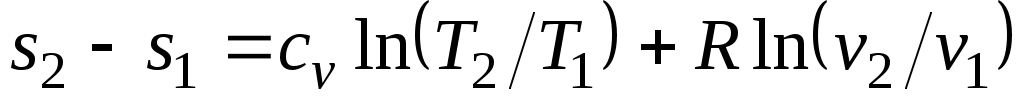 . (3.5) . (3.5)
Из уравнения Клапейрона, записанного для состояний 1 и 2, следует:
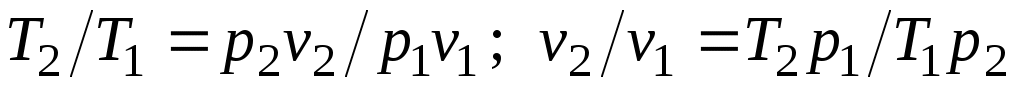 . .
После подстановки отношений и в выражение (3.4) получим следующие формулы для изменения энтропии идеального газа:
 ; ;
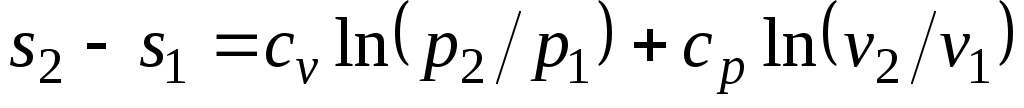 . (3.6) . (3.6)
Поскольку энтропия есть функция состояния рабочего тела, уравнениями (3.5) — (3.6) можно пользоваться вне зависимости от пути перехода рабочего тела между состояниями 1 и 2 и, в частности, от того, равновесный этот переход или нет.

Рисунок 3.2 - Графическое изображение теплоты в T, s– координатах
Понятие энтропии позволяет ввести чрезвычайно удобную для термодинамических расчетов Т, s-диаграмму, на которой (как и на p,v -диаграмме) состояние термодинамической системы изображается точкой, а равновесный термодинамический процесс линией (Рисунок 3.2).
В равновесном процессе
 ; ;
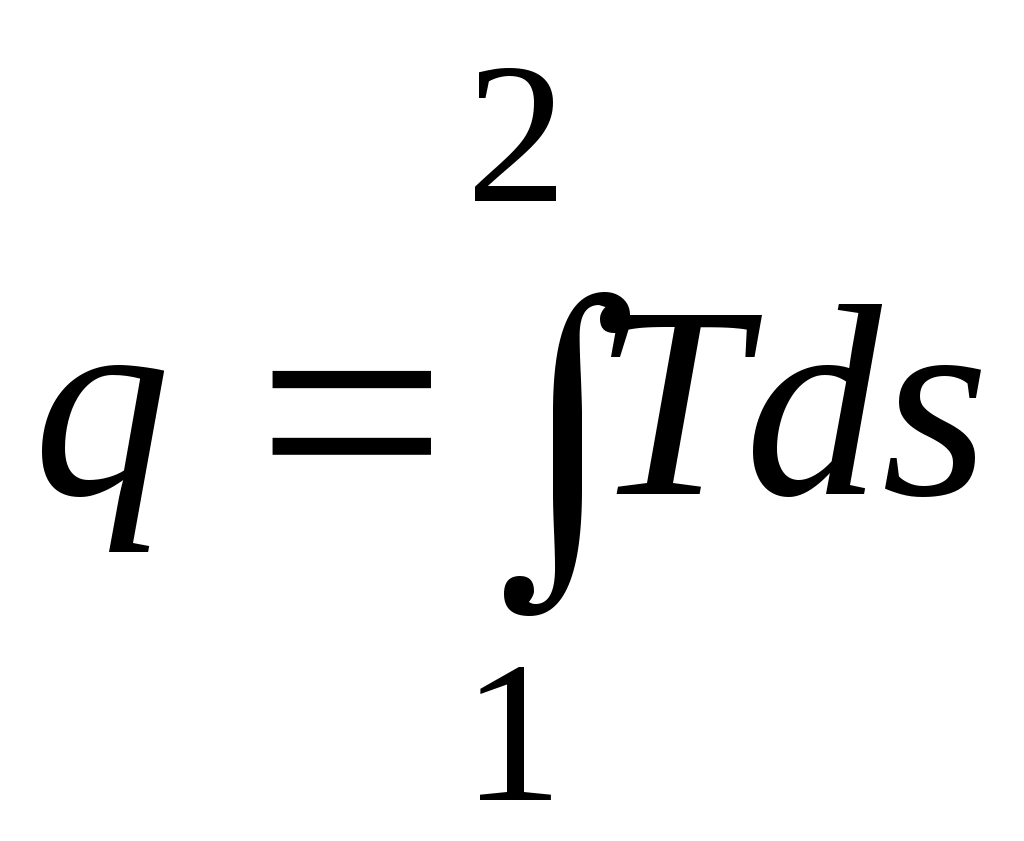 . .
Очевидно, что в Т, s-диаграмме элементарная теплота процесса  изображается элементарной площадкой с высотой Т и основанием ds, а площадь, ограниченная линией процесса, крайними ординатами и осью абсцисс, эквивалентна теплоте процесса. изображается элементарной площадкой с высотой Т и основанием ds, а площадь, ограниченная линией процесса, крайними ординатами и осью абсцисс, эквивалентна теплоте процесса.
Формула  показывает, что dsи показывает, что dsи  имеют одинаковые знаки, следовательно, по характеру изменения энтропии в равновесном процессе можно судить о том, в каком направлении происходит теплообмен. При подводе теплоты к телу ( имеют одинаковые знаки, следовательно, по характеру изменения энтропии в равновесном процессе можно судить о том, в каком направлении происходит теплообмен. При подводе теплоты к телу ( >0) его энтропия возрастает (ds>0), а при отводе теплоты ( >0) его энтропия возрастает (ds>0), а при отводе теплоты ( <0) — убывает (ds<0). <0) — убывает (ds<0).
17. Уравнение Майера.
внутренняя энергия идеального газа определяется только его температурой и не зависит от объема, поэтому 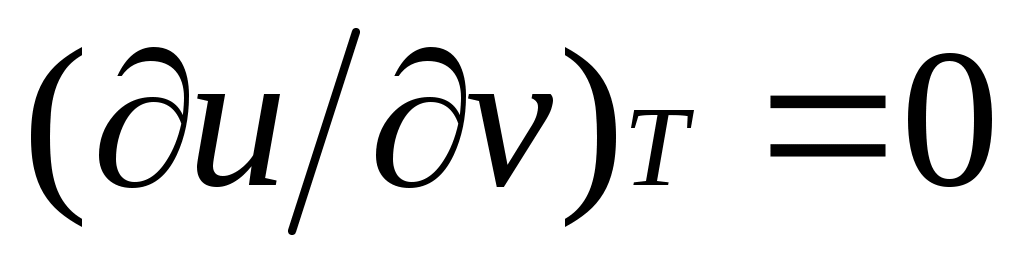 и, кроме того, из уравнения состояния следует и, кроме того, из уравнения состояния следует 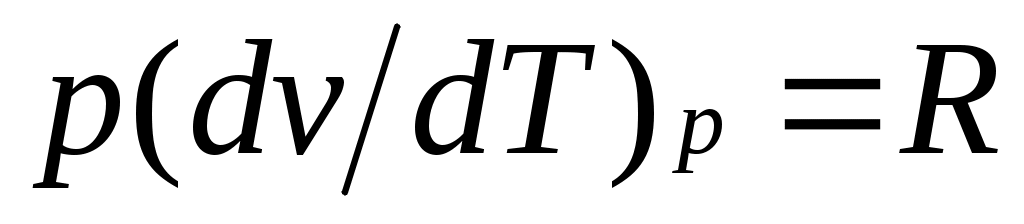 , откуда , откуда
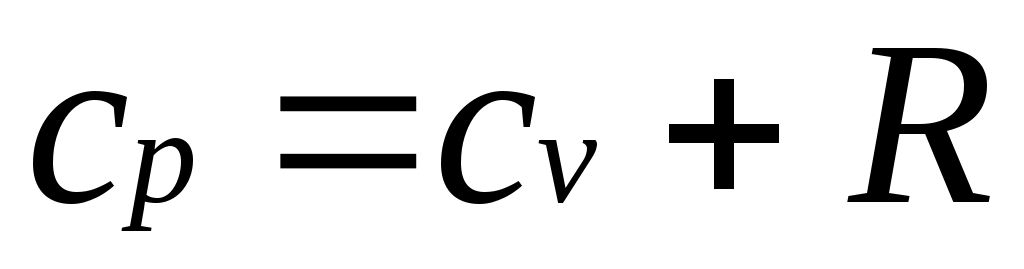 . .
Это соотношение называется уравнением Майера и является одним из основных в технической термодинамике идеальных газов.
18. Цикл Карно.
Рассмотрим простейший случай, когда имеется один горячий с температурой T1 и один холодный с температурой T2 источники теплоты. Теплоемкость каждого из них столь велика, что отъем рабочим телом теплоты от одного источника и передача ее другому практически не меняет их температуры.
цикл, состоящий из двух изотерм и двух адиабат, носит название цикла К а р н о, поскольку именно с его помощью С. Карно в 1824 г. установил основные законы превращения тепловой энергии в механическую.
Осуществление цикла Карно в тепловой машине можно представить следующим образом. Газ (рабочее тело) с начальными параметрами, характеризующимися точкой а, помещен в цилиндр под поршень, причем боковые стенки цилиндра и поршень абсолютно нетеплопроводны, так что теплота может передаваться только через основание цилиндра.
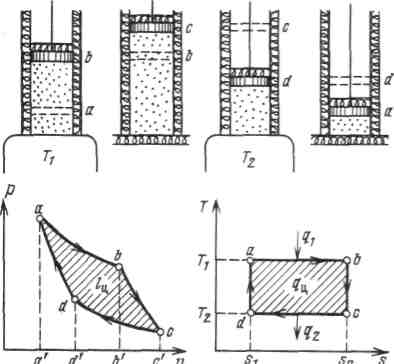
Рисунок 4.3 - Прямой цикл Карно
Вводим цилиндр в соприкосновение с горячим источником теплоты. Расширяясь изотермически при температуре от объема vaдо объема vb, газ забирает от горючего источника теплоту 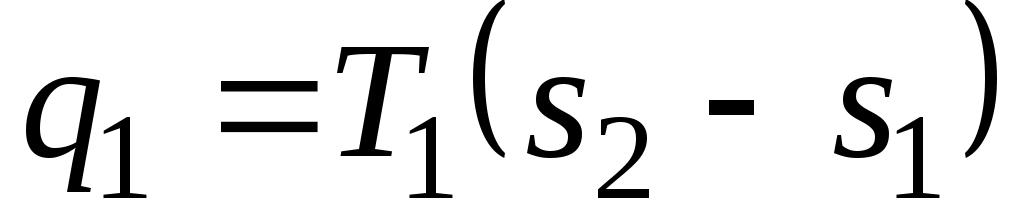 .В точке bподвод теплоты прекращаем и ставим цилиндр на теплоизолятор. Дальнейшее расширение рабочего тела происходит адиабатно. Работа расширения совершается при этом только за счет внутренней энергии, в результате чего температура газа падает до T2. .В точке bподвод теплоты прекращаем и ставим цилиндр на теплоизолятор. Дальнейшее расширение рабочего тела происходит адиабатно. Работа расширения совершается при этом только за счет внутренней энергии, в результате чего температура газа падает до T2.
Теперь возвратим тело в начальное состояние. Для этого сначала поместим цилиндр на холодный источник с температурой T2 и будем сжимать рабочее тело по изотерме cd, совершая работу l2 и отводя при этом к нижнему источнику от рабочего тела теплоту 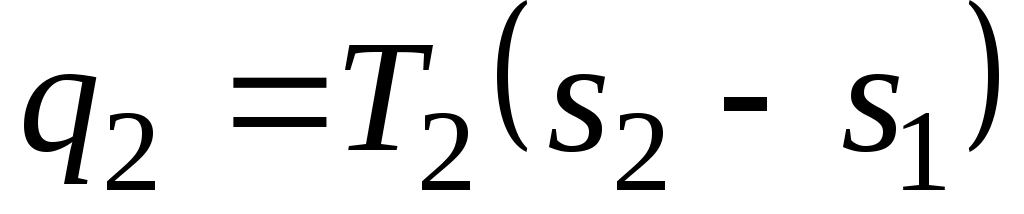 . Затем снова поставим цилиндр на теплоизолятор и дальнейшее сжатие проведем в адиабатных условиях. Работа, затраченная на сжатие по линии da, идет на увеличение внутренней энергии, в результате чего температура газа увеличивается до T1. . Затем снова поставим цилиндр на теплоизолятор и дальнейшее сжатие проведем в адиабатных условиях. Работа, затраченная на сжатие по линии da, идет на увеличение внутренней энергии, в результате чего температура газа увеличивается до T1.
Таким образом, в результате цикла каждый килограмм газа получает от горячего источника теплоту q1, отдает холодному теплоту q2 и совершает работу lц.
Подставив в формулу  , справедливую для любого цикла, выражения для q1и q2,получим, что термический КПД цикла Карно определяется формулой , справедливую для любого цикла, выражения для q1и q2,получим, что термический КПД цикла Карно определяется формулой
 . .
Из нее видно, что термический КПД цикла Карно зависит только от абсолютных температур горячего и холодного источников. Увеличить КПД цикла можно либо за счет увеличения температуры горячего источника, либо за счет уменьшения температуры холодного, причем влияние температур и на значение различно:
 , ,
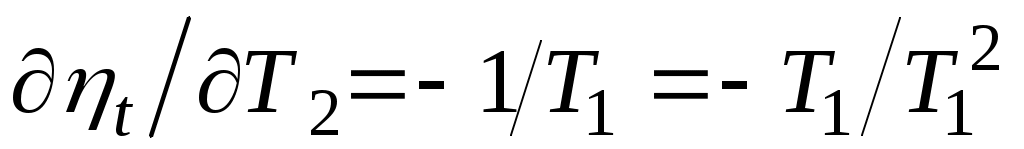 , ,
а так как  . .
Таким образом, увеличение температуры горячего источника в меньшей степени повышает КПД цикла Карно, чем такое же (в Кельвинах) уменьшение температуры холодного.
Являясь следствием второго закона термодинамики, формула для КПД цикла Карно, естественно, отражает его содержание. Из нее видно, что теплоту горячего источника можно было бы полностью превратить в работу, т. е. получить КПД цикла, равный единице, лишь в случае, когда  либо либо 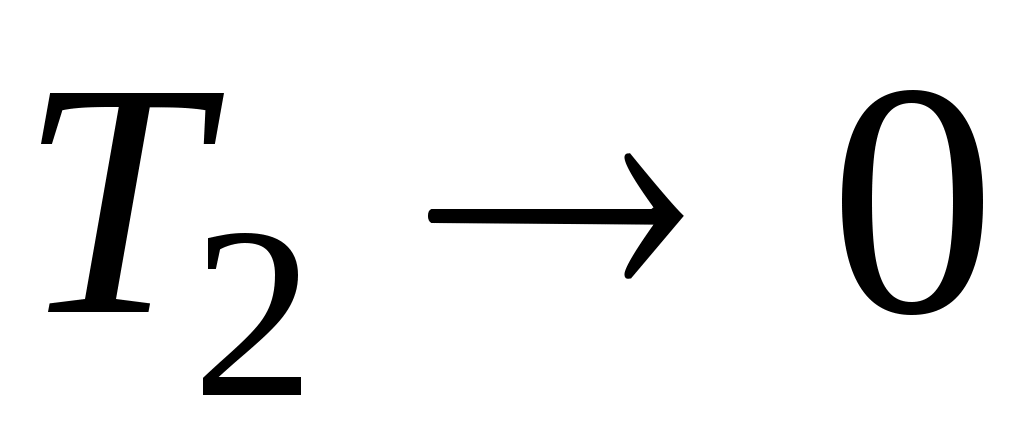 . Оба значения температур недостижимы. (Недостижимость абсолютного нуля температур следует из третьего начала термодинамики). . Оба значения температур недостижимы. (Недостижимость абсолютного нуля температур следует из третьего начала термодинамики).
При T1=T2 термический КПД цикла равен нулю.
Это указывает на невозможность превращения теплоты в работу, если все тела системы имеют одинаковую температуру, т. е. находятся между собой в тепловом равновесии. Для ориентировки приводим значения термического КПД цикла Карно при различных температурах горячего источника и при температуре холодного источника, равной 10 °С.
t,°С
|
200
|
400
|
600
|
800
|
1000
|
1200
|
1400
|
1600
|

|
0,40
|
0,58
|
0,68
|
0,74
|
0,78
|
0,81
|
0,83
|
0,85
|
Приведенные цифры дают КПД идеального цикла. Коэффициент полезного действия реального теплового двигателя, конечно, ниже.
|
|
|
 Скачать 1.23 Mb.
Скачать 1.23 Mb.

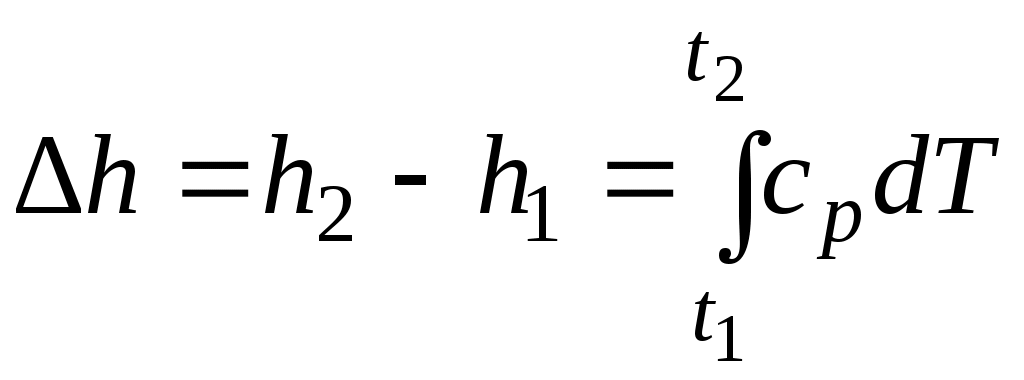 .
. ассмотрим газ массой М и объемом V, заключенный в эластичную оболочку
ассмотрим газ массой М и объемом V, заключенный в эластичную оболочку 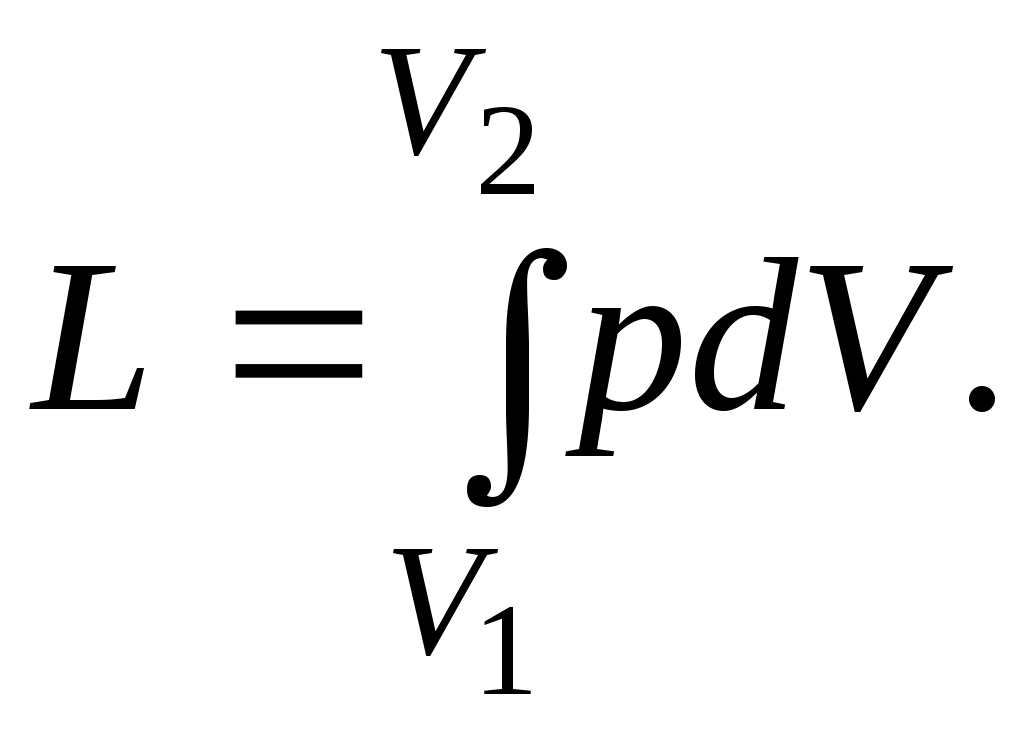
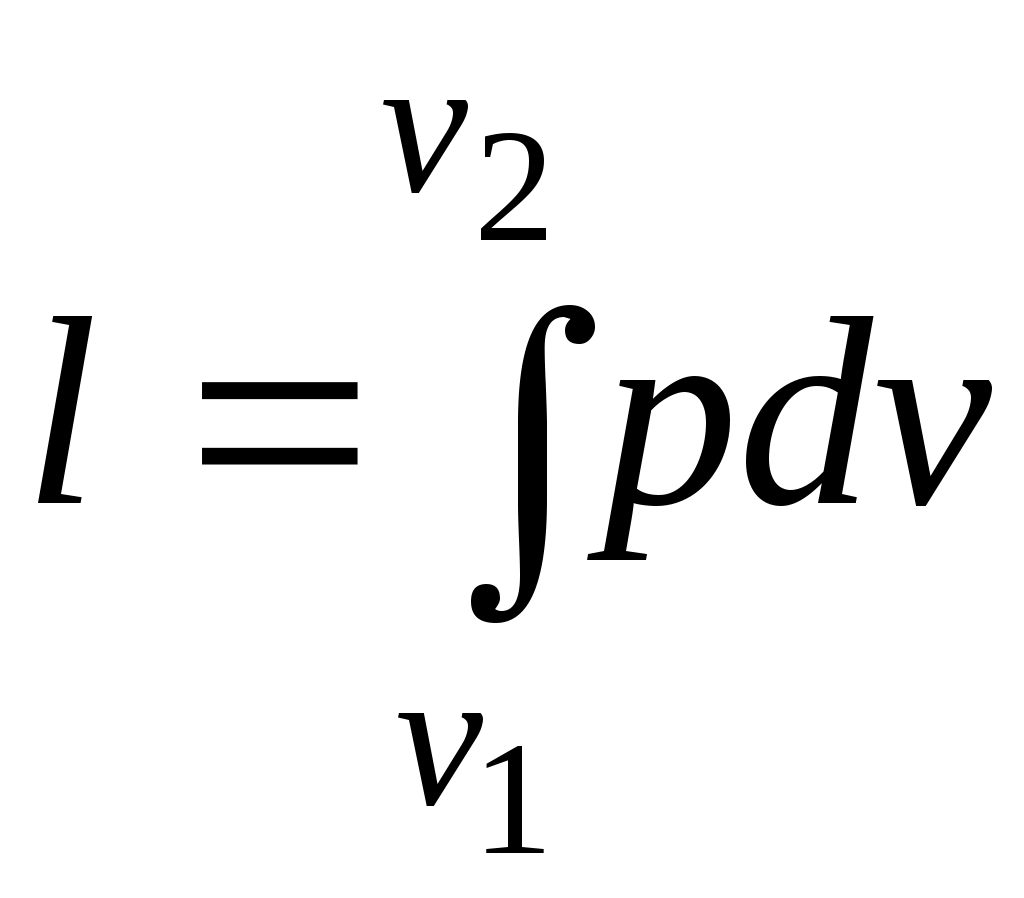 . (3.2)
. (3.2)

