курсовая. Техническое задание 8 2 Расчет принципиальной схемы фнч и выбор компонентов
 Скачать 475.45 Kb.
|
   ОглавлениеВведение 5 1 Техническое задание 8 2 Расчет принципиальной схемы ФНЧ и выбор компонентов 10 2.1 ФНЧ первого порядка 10 2.2 ФНЧ второго порядка 12 2.3 ФНЧ четвертого порядка 18 2.4 Расчет параметров элементов схемы ФНЧ первого порядка 22 2.5 Расчет параметров элементов схемы ФНЧ второго порядка 24 2.6 Расчет параметров элементов схемы ФНЧ четвертого порядка 27 2.7 Выбор операционного усилителя 32 3 Исследование характеристик фильтра 35 3.1 Исследование ФНЧ Баттерворта первого порядка 35 3.2 Исследование ФНЧ Баттерворта второго порядка 40 3.3 Исследование ФНЧ Баттерворта четвертого порядка 46 Вывод 55 Список использованных источников 57 ВведениеФильтром называется электронная схема, пропускающая или усиливающая синусоидальные сигналы в определенном диапазоне частот и ослабляющая сигналы с частотами, выходящими за пределы заданного диапазона. Область применения фильтров в электронике и вычислительной технике очень широка и схемы отличаются большим разнообразием. Простые пассивные фильтры строятся на основе таких элементов как: резисторы, конденсаторы и катушки индуктивности. Более сложные активные на базе операционных усилителей и цепей из резисторов и конденсаторов. Активными фильтрами принято называть схемы, состоящие из резисторов, конденсаторов и операционных усилителей в качестве активных элементов. За счет высокого входного сопротивления ОУ (МОм), его коэффициента усиления (104-106) и малого выходного сопротивления (десятки Ом) удалось резко повысить качественные показатели активных фильтров при совместном применении с пассивными RC-цепями. Различают фильтры нижних частот, верхних частот и полосовые фильтры. Основные параметры фильтров можно определить по амплитудно-частотным характеристикам (АЧХ). Основными параметрами фильтров нижних и верхних частот являются коэффициент передачи в полосе пропускания K0, частота среза fс, соответствующая уровню 0,707K0, а также наклон АЧХ в полосе ограничения и неравномерность в полосе пропускания. Для полосовых фильтров параметрами являются коэффициент передачи K0 на частоте резонанса f0 и добротность  , где ∆f - полоса пропускания на уровне 0,707K0.АЧХ фильтра Баттерворта монотонно убывает с ростом частоты. По этой причине его называют фильтром с максимально плоскими характеристиками. АЧХ фильтра Баттерворта так же имеет довольно длинный горизонтальный участок и резко спадает за частотой среза. Переходная характеристика такого фильтра при ступенчатом входном сигнале имеет колебательный характер. С увеличением порядка фильтра колебания усиливаются. Цель работы: проектирование активных фильтров Баттерворта нижних частот первого, второго и четвертого порядков в соответствии с техническим заданием, расчет их передаточных характеристик. 1 Техническое заданиеРассчитать фильтры низкой частоты со следующими параметрами:
2 Расчет принципиальной схемы ФНЧ и выбор компонентов2.1 ФНЧ первого порядкаАктивный фильтрнижних частот первого порядка на основе инвертирующего усилителя представлен на рисунке 1. 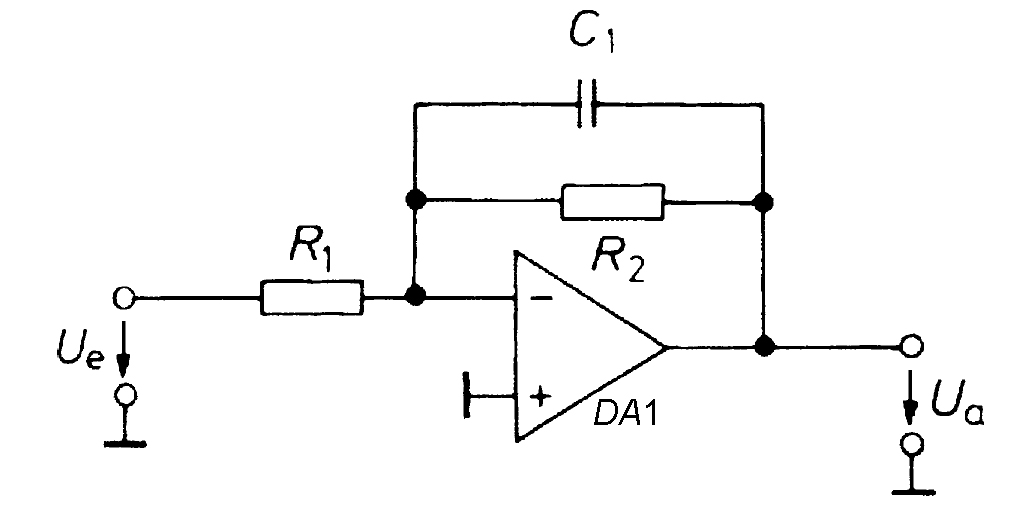 Рисунок 1 – ФНЧ первого порядка на основе инвертирующего усилителя Передаточная функция фильтра нижних частот первого порядка в общем случае имеет вид:  , (1)где a1 – коэффициент передаточной функции, K0 – коэффициент усиления фильтра в полосе пропускания,  , 0 – частота среза.Передаточная функция фильтра нижних частот первого порядка имеет вид:  . (2)Откуда вытекают формулы для расчета:  , (3) . (4)Для расчета параметров схемы (R1 и R2) необходимо задать частоту среза, отрицательный, в данном случае, коэффициент передачи постоянного напряжения K0 и емкость C1. Приравнивая коэффициенты передаточной функции к коэффициентам в выражении (1), получаем:  , (5) . (6)2.2 ФНЧ второго порядкаАктивный фильтрнижних частот второго порядка на основе схемы Рауха (с многопетлевой отрицательной обратной связью) представлен на рисунке 2. 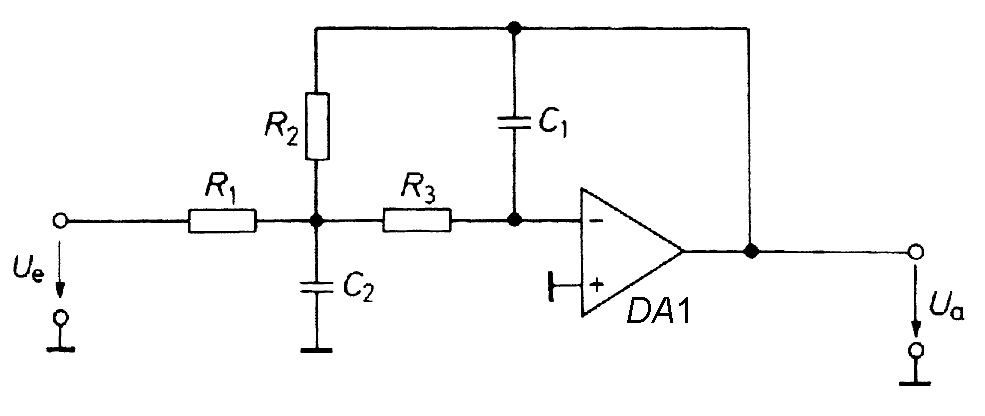 Рисунок 2 – ФНЧ второго порядка на основе схемы Рауха Передаточная функция фильтра нижних частот второго порядка в общем случае имеет вид:  . (7)Передаточная функция фильтра нижних частот второго порядка в общем случае имеет вид:  . (8)С учетом коэффициентов уравнения (7) получаем систему уравнений для расчета параметров фильтра:  , (9) , (10) . (11)Для определения параметров фильтра можно, например, задать сопротивления резисторов R1 и R3 и по расчетным формулам вычислить значения R2, C1 и C2. Как видно, такой расчет параметров возможен для всех положительных значений a1 и b1. Следовательно, можно реализовать любой желаемый тип фильтра. Коэффициент передачи постоянного сигнала K0 является отрицательным, поэтому фильтр на низких частотах инвертирует сигнал. При переходе от расчетных значений сопротивлений и емкостей RC-цепей следует учитывать конструктивные и технологические особенности элементов. Выполнить подбор сопротивлений резисторов достаточно легко, так как они выбираются из стандартных рядов номинальных значений, например ряда Е24: 10, 11, 12, 13, 14, 15, 16, 18, 20, 22, 24, 27, 30, 33, 36, 39, 43, 47, 51, 56, 62, 68, 82, 91. Конденсаторы устанавливаются из стандартного ряда Е12: 10, 12, 15, 18, 22, 27, 30, 33, 39, 47, 56, 68, 82. Используемые значение сопротивления и емкости из ряда могут быть умножены на  , где n – целое положительное число или нуль. Например, можно использовать резисторы: 13 Ом, 130 Ом, 1,3 кОм, 13 кОм, 130 кОм и т.д.Использовать в схеме резисторы с сопротивлением менее 1 кОм нежелательно так как это неминуемо приведет к увеличению энергопотребление схемы и затруднит выбор операционного усилителя. При этом лучше при расчете фильтра выбрать номинал конденсатора и вычислить сопротивления резисторов. Для этого решим уравнения относительно сопротивлений и получим:  , (12) , (13) . (14)Для того, чтобы сопротивление резистора R2 было действительным, должно выполняться условие:  . (15)Благоприятные расчетные параметры получаются, когда задают значение  и выбирают следующее по величине нормированное значение  . Параметры фильтра относительно слабо зависят от точности номиналов компонентов схемы. Эту схему рекомендуют для реализации фильтров с высокой добротностью.Чтобы операционной усилитель мог считаться идеальным, на частоте среза фильтра он должен иметь высокий коэффициент петлевого усиления. По этой причине даже при низких частотах среза требуются быстродействующие операционные усилители. Выбор усилителя необходимо выполнять исходя из следующих условий:
где Rmin и Rmax – соответственно номиналы минимального и максимального резисторов в схеме спроектированного фильтра, fT – частота единичного усиления. 2.3 ФНЧ четвертого порядкаЕсли в области среза амплитудно-частотная характеристика фильтра недостаточно крута, следует применять фильтр более высокого порядка. Для этого последовательно включают фильтры первого и второго порядков. При этом амплитудно-частотные характеристики отдельных фильтров перемножаются. Однако было бы неправильно, например, включать последовательно два одинаковых фильтра Баттерворта второго порядка, чтобы получить фильтр Баттерворта четвертого порядка. Получающийся при этом фильтр имел бы другую частоту среза и другую амплитудно-частотную характеристику. Поэтому необходимо задавать коэффициенты отдельных фильтров так, чтобы произведение амплитудно-частотных характеристик соответствовало желаемому оптимальному типу фильтра. Для упрощения расчета отдельных фильтров (звеньев) полиномы передаточных функций различных типов фильтров разлагаются в ряд. Коэффициенты a1 и b1 отдельных звеньев фильтра известны. Каждый коэффициент при bi≠ 0 можно реализовать на основе одного описанного фильтра второго порядка. Необходимо лишь заменить их коэффициенты a1 и b1 на коэффициенты aiи bi. Для расчета параметров схемы следует подставить в данные формулы желаемую частоту среза результирующего фильтра. Отдельные звенья фильтра, как правило, имеют разные частоты среза. Фильтры нечетного порядка содержат член с bi= 0. Этот член можно реализовать на основе описанного фильтра первого порядка, причем a1 следует заменить на ai. Также здесь вместо значения fgнужно подставить частоту среза результирующего фильтра. Для звеньев фильтра автоматически выбирают значение ai, соответствующее частоте среза fgi. В принципе, безразлично, в каком порядке расположены отдельные звенья фильтра, так как результирующая амплитудно-частотная характеристика в любом случае будет одной и той же. На практике, однако, существуют различные точки зрения относительно последовательности включения звеньев фильтра. Например, с точки зрения перегрузки схемы лучше располагать звенья фильтра в порядке возрастания частоты среза и фильтр с меньшей частотой среза включать на входе. В противном случае уже первый каскад может оказаться перегруженным, тогда как на выходе второго каскада уровень сигнала будет меньше предельного. Это происходит потому, что звенья фильтра с более высокой частотой среза всегда имеют более высокую добротность полюсов и, следовательно, подъем амплитудно-частотной характеристики вблизи частоты среза. Меньшая перегрузка схемы соответствует случаю, когда звенья с меньшей частотой среза находятся в начале цепочки фильтров. Другая точка зрения относительно порядка расположения звеньев фильтра может быть связана с шумами. В этом случае желательна обратная последовательность включения звеньев, потому что фильтры с меньшей частотой среза в конце цепочки ослабляют шумы входных каскадов. На рисунке 3 приведена схема ФНЧ Баттерворта четвертого порядка, составленная из двух звеньев ФНЧ второго порядка.  Рисунок 3 – ФНЧ четвертого порядка на основе двух ФНЧ второго порядка2.4 Расчет параметров элементов схемы ФНЧ первого порядкаПроизведем расчет параметров элементов ФНЧ (рисунок 1) по формулам (2), (5), (6). Задаем исходные данные: a1=1 f0=40 кГц 0=2  f00=2.513*105  K0=26 Выбираем номинал С1 из ряда Е12: C1=30*10-12 Ф Находим по формулам (5), (6) значения сопротивлений: R1=5.101*103 Ом R2=1.326*105 Ом Из ряда Е24 выбираем: R1=5100 Ом R2=130000 Ом Рассчитываем характеристики фильтра (АЧХ, ФЧХ) в диапазоне от нуля до 100кГц:  =  В логарифмическом масштабе  = 20  = arg( Итоговые номинальные значения: C1=30 пФ; R1=5100 Ом; R2=130 кОм; 2.5 Расчет параметров элементов схемы ФНЧ второго порядкаПроизведем расчет параметров элементов ФНЧ (рисунок 2) по формулам (8), (12), (13), (14), (15). Задаем исходные данные: a1=1 b1=1.4142 f0=40 кГц 0=2 f0 0=2.513*105 K0= − 26 Из ряда Е12 выбираем: C1=18*10-12 Ф Для того, чтобы сопротивление резистора R2 было действительным, рассчитываем С2 по формуле:   Ф Из ряда Е12 выбираем:  ФРассчитываем сопротивления:   Ом  Ом = = Ом Из ряда Е24 выбираем:  =  Рассчитываем характеристики фильтра (АЧХ, ФЧХ) в диапазоне от 0 до 100 кГц: K(f)=  В логарифмическом масштабе: = 20 = arg(Итоговые номинальные значения: R1 = 5.1 кОм, R2 = 130 кОм, R3 = 6.8 кОм, С1 = 18 пФ, С2 = 1.8 нФ. 2.6 Расчет параметров элементов схемы ФНЧ четвертого порядкаПроизведем расчет параметров элементов для двух ФНЧ второго порядка (рисунок 3) по формулам (8), (12), (13), (14), (15). Для первого ФНЧ выбираем коэффициент K01 = -2, для второго K02= -13. Расчеты производятся аналогично расчетам, приведенным в параграфе 2.5. Расчет параметров для первого звена ФНЧ четвертого порядка. a1=1.8478; a2=0.7654 b1=1.0000; b2=1.0000 k1=0.719; k2=1.390 K01= −2; K02= −13. f0=40 кГц 0i=ki2  01=1.807*105 ; 02=3.493*105 hi=  ;h1=3.515 h2=95.59. Из доступных номиналов выбираем емкости С: С11=12-9 Ф; С12=12-10 Ф; С2i=1.5hiС1i С21=1.163*10-9 Ф; С22=2.326*10-9 Ф; R2i=  R21=9.402*103 Ом; R22=2.85*104 Ом; R1i=  R11=4.701*103 Ом; R12=2.192*103 Ом; R3i=  R31=1.445*104 Ом; R32=7.654*103 Ом; n=103 j=1..n f1=100 fj+1=fj  (2f0)1/nРасчет АЧХ: K1(  = K2( = Передаточную функцию для ФНЧ четвертого порядка, составленную из двух звеньев ФНЧ второго порядка, получаем перемножением передаточных функций этих звеньев: K(  K1( K2(Расчет ФЧХ: A(f)=  Итоговые номинальные значения: R1=4.7 103 Ом; R4=2.2103 Ом;R2=9.1 103 Ом; R5=2.7104 Ом;R3=1.4 104 Ом; R6=8.2103 Ом;С1=2.2 10-10 Ф; С3=1.210-9 Ф;С2=18 10-12 Ф; С4=2.710-9 Ф;2.7 Выбор операционного усилителяДля выбора операционного усилителя определим номиналы минимального и максимального сопротивлений в схемах. Таким образом, определим операционный усилитель, который будет подходить для всех схем фильтров. Параметры операционного усилителя определяются условиями (16), (17), (18). Из приведенных расчетов получаем: Для фильтра первого порядка: Rmin=5100 Ом= 5.1 кОм, Rmax= 1.3 105 Ом= 130 кОм.Следовательно, параметры усилителя должны удовлетворять:  , , .Для фильтра второго порядка: Rmin=5100 Ом=5.1 кОм, Rmax= 130000 Ом=130 кОм. Следовательно, параметры усилителя должны удовлетворять: , ,.Для фильтра четвертого порядка: Rmin=2200 Ом=2.2 кОм, Rmax= 27000 Ом=27 кОм. Следовательно, параметры усилителя должны удовлетворять:  , ,.Таким образом, для рассчитанных параметров подходит операционный усилитель К544УД2А, имеющий следующие характеристики:  , ,fT ≥ 15 МГц. Подходящими параметрами обладают также усилители К544УД2Б, К544УД2В, усилители серии К574УД1(А, Б, В). 3 Исследование характеристик фильтра3.1 Исследование ФНЧ Баттерворта первого порядкаИсходя из расчетов параметров элементов ФНЧ приведенных в параграфе 2.4, окончательная принципиальная схема фильтра показана на рисунке 4. Используемые элементы прописаны в таблице 1. Рисунок 4 – Принципиальная схема ФНЧ Баттерворта первого порядка Таблица 1.
На рисунке 5 приведена АЧХ ФНЧ Баттерворта первого порядка, по горизонтали приведены значения частоты от 0 до 100000 Гц, а по вертикали модуль передаточной функции в дБ. На графике помечены уровни, соответствующие максимальному значению (28,35 дБ) и уровню на частоте среза 40000 Гц (25,4 дБ). Разница между ними составляет 3.05 дБ.  Рисунок 5 – АЧХ ФНЧ Баттерворта первого порядка На рисунке 6 приведена ФЧХ ФНЧ Баттерворта первого порядка. По горизонтали отложена частота от 0 до 100000 Гц, а по вертикали фаза.  Рисунок 6 – ФЧХ ФНЧ Баттерворта первого порядка 3.2 Исследование ФНЧ Баттерворта второго порядкаИсходя из расчетов параметров элементов ФНЧ Баттерворта второго порядка приведенных в параграфе 2.5, окончательная принципиальная схема фильтра показана на рисунке 7. Используемые элементы прописаны в таблице 2. Ниже представлена принципиальная схема фильтра. Рисунок 7 – Принципиальная схема ФНЧ Баттерворта второго порядка Таблица 2.
На рисунке 8 приведена АЧХ ФНЧ Баттерворта второго порядка, по горизонтали приведены значения частоты от 0 до 100000 Гц, а по вертикали модуль передаточной функции в дБ. На графике помечены уровни, соответствующие среднему значению в полосе пропускания (28.2 дБ) и уровню на частоте среза 40000 Гц (25.225 дБ). Разница между ними составляет 3 дБ. На рисунке 9 приведена ФЧХ ФНЧ Баттерворта второго порядка. По горизонтали отложена частота от 100 до 1000000 Гц, а по вертикали фаза. В расчетном диапазоне частот изменения фазы составляет от до 0,5.  Рисунок 8 – АЧХ ФНЧ Баттерворта второго порядка Ниже представлена ФЧХ фильтра второго порядка.  Рисунок 9 – ФЧХ ФНЧ Баттерворта второго порядка 3.3 Исследование ФНЧ Баттерворта четвертого порядкаИсходя из расчетов параметров элементов ФНЧ Чебышева четвертого порядка, приведенных в параграфе 2.6, окончательная принципиальная схема фильтра показана на рисунке 10. Используемые элементы прописаны в таблице 3. Ниже представлена принципиальная схема фильтра. Рисунок 10 – Принципиальная схема ФНЧ Баттерворта четвертого порядка Таблица 3.
На рисунке 11 приведена АЧХ двух звеньев ФНЧ Баттерворта четвертого порядка, по горизонтали приведены значения частоты от 100 до 10000000 Гц, а по вертикали модуль передаточной функции в дБ. Сплошной – для первого звена, пунктирной – для второго звена.  Рисунок 11 – АЧХ двух звеньев ФНЧ Баттерворта четвертого порядка Как видно из графика, максимальные значения АЧХ двух звеньев различны, это объясняется разными значениями коэффициента усиления. На графике также отмечены частоты срезов звеньев: для первого звена ��1 = 28759 Гц (3 дБ), для второго – ��2 = 55592 Гц (19 дБ). Можно заметить, что начальная частота среза фильтра, равная 40 кГц, находится между данными значениями. На рисунке 12 приведен график АЧХ всего фильтра, и ФЧХ. Сплошной – амплитудно-частотная характеристика, пунктирной – фазочастотная характеристика. По горизонтали отложена частота от 100 до 10000000 Гц, по вертикали на левой оси модуль передаточной функции в дБ, а на правой - фаза. На графике отмечена точка максимального значения характеристики (28,4 дБ), а также точка, соответствующая частоте среза 40 кГц (25,6 дБ).   Рисунок 12 – АЧХ и ФЧХ ФНЧ Баттерворта четвертого порядка Ниже представлены АЧХ двух звеньев и АЧХ всего фильтра на одном графике.  Рисунок 13 – АЧХ: всего фильтра и отдельных звеньев ВыводПри выполнении курсовой работы были выбраны схемы активных фильтров Баттерворта низких частот 1, 2 и 4 порядков. Рассчитаны номиналы элементов цепи, при которых характеристики фильтров удовлетворяют техническому заданию. Выбран операционный усилитель К544УД2А, параметры которого обеспечивают предъявляемые к активному элементу требования по входному и выходному сопротивлению, а также по частоте единичного усиления. Исходя из найденных значений параметров элементов, с учетом ряда номиналов конденсаторов Е12 и ряда номиналов резисторов Е24, построены АЧХ и ФЧХ фильтров низких частот. Исследование характеристик показало, что они полностью удовлетворяют техническому заданию с точность 5%. Таким образом, можно сделать вывод, что значения элементов фильтров подобраны правильно. Список использованных источников
|
; (16)
; (17)
, (18)