Сапромат Курсовая задание вариант 9, аэрокосмический факультет. Техническое задание Ри Схема нагружения вала Табл. 1 Исходные данные Примечание. Состояние поверхности 1 полирование, 2 шлифование, 3 тонкое точение, 4 грубое точение, 5 наличие окалины. 3
 Скачать 119.88 Kb. Скачать 119.88 Kb.
|
|
1 Техническое задание 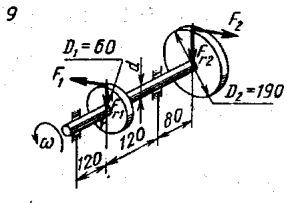 Рис1. Схема нагружения вала 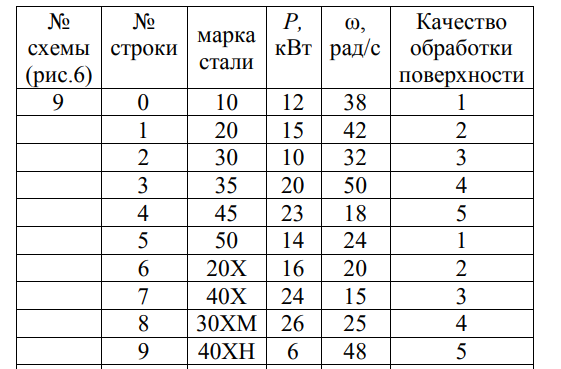 Табл. 1 Исходные данные Примечание. Состояние поверхности: 1 – полирование, 2 – шлифование, 3 – тонкое точение, 4 – грубое точение, 5 – наличие окалины. 3 2 Расчетная часть 2.1 Расчет на прочность вала при изгибе с кручением. Для ведущего вала прямозубой цилиндрической передачи редуктора с двумя зубчатыми колесами (рис. 1), передающего мощность Р, 6 кВт, при угловой скорости , 48 рад/с (числовые значения этих величин взяты, согласно варианта из табл. 1) определить вертикальные и горизонтальные составляющие реакций подшипников. Fr1 = 0,4F1; Fr2 = 0,4F2. 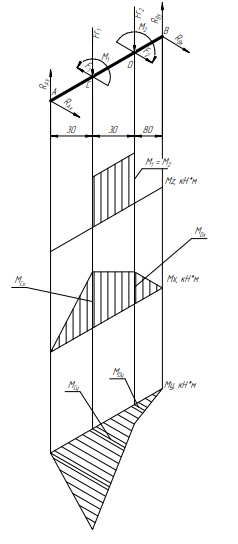 4 Составляем расчетную схему вала, приводя действующие на вал нагрузки к оси (рис. 2, б). При равномерном вращении вала: М1 = М2, где М1 и М2 — скручивающие пары, которые добавляются при переносе сил F1 и F2 на ось вала. Определяем вращающий момент, действующий на вал: М1 = М2 = P/ = 0,125·103 Н·м = 0,125 кН·м. Вычислим нагрузки, приложенные к валу: F1 = 2M1/d1 = 2·0,125·103 /0,06 = 4,17·103Н = 4,17 кН; Fr1 = 0,4·4,17 = 1,67 кН; F2 = 2M2/d2 = 2·0,125·103 /0,19 = 1,3·103Н = 1,3 кН; Fr2 = 0,4·1,3 = 0,52 кН; Определяем реакции опор в вертикальной плоскости (рис. 2, б): МА = Fr1·АС+ Fr2·АD –RBy·AB= 0; RBy= (Fr1·АС+ Fr2·АD)/AB = (1,67·0,12+0,52·0,24)/0,32 = 1,02 кН; МB = RAy·AB – Fr1·BС– Fr2·DB = 0; RAy= (Fr1·BС + Fr2·DB)/AB = (0,52·0,08+1,67·0,2)/0,32 = 1,17 кН; Y = RAy – Fr1 – Fr2 +RBy= 1,17 – 1,67 – 0,52 + 1,17 = 0. Y = 0, следовательно, RAy и RBy найдены правильно. Определяем реакции опор в горизонтальной плоскости (рис. 2, б): МА = F1·АС – F2·АD –RBx·AB= 0; RBx= (F1·АС– F2·АD)/AB = (4,17·0,12 – 1,3·0,24)/0,32 = 0,59 кН; МB = RAx·AB – F1·СB + F2·DB = 0; RAx= (F1·СB – F2·DB)/AB = (4,17·0,2 – 1,3·0,08)/0,32 = 2,28 кН; X = RAx – F1 + F2 + RBx= 2,28 – 4,17+ 1,3 + 0,59 = 0. 5 X = 0, следовательно, RAx и RBx найдены верно. На основе полученных ранее данных, строим эпюру крутящих моментов(рис.2 б). Определяем в характерных сечениях значения изгибающих моментов Мх в вертикальной плоскости и Му в горизонтальной плоскости и строим эпюры (рис. 2, г, д): МСх= RAy·АС = 1,17·0,12 = 0,14 кН·м; МDх= RAy·AD – Fr1·СD = 1,17·0,24 – 1,67·0,12 = 0,08 кН·м; МСy= RAx·АС = 2,28·0,12 = 0,274 кН·м; МDу= RAх·AD – F1·СD = 2,28·0,24 – 4,17·0,12 = 0,047 кН·м. Вычисляем наибольшее значение эквивалентного момента по заданным гипотезам прочности. Так как в данном примере значение суммарного изгибающего момента в сечении С больше, чем в сечении D, MИс = 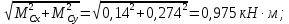 MИD = 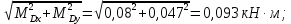 то сечение С и является опасным. Определяем эквивалентный момент в сечении С, согласно гипотезе потенциальной энергии формоизменения: МЭКВⅣ = 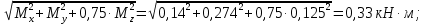 Вычисляем допускаемое нормальное напряжение: [𝜎] = 𝜎т /[𝑛] = 800/2 = 400 МПа, где 𝜎т = 800МПа, (согласно табл.1, Приложения методических указаний) [1, с.21]. Определяем требуемые размеры вала: 6 d = 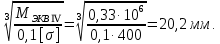 Принимаем dвала = 20мм. 2.2 Расчет вала на сопротивление многоцикловой усталости. Определяем требуемые размеры вала на участках AC, СD и DB. Допускаемые напряжения при действии знакопеременных нагрузок значительно ниже, чем в случае статической нагрузки (примерно в 1,9). Для стали 40ХН примем [σ]p = 160МПа [2, с. 264]. I участок АС: 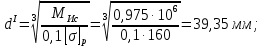 Принимаем стандартное значение d = 40 мм. II участок СD: 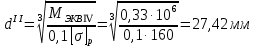 ; ;Принимаем стандартное значение d = 28 мм. III участок DB: 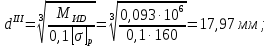 Принимаем стандартное значение d = 20 мм. На II участке CD диаметр вала рассчитан в I части курсовой работы dII = 20 мм. Определение геометрических характеристик опасных сечений вала: 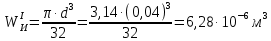 ; ;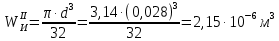 ; ;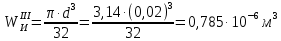 , ,с учетом ослабления пазами для двух стандартных шпонок (табл. 3 приложения методических указаний) [1, с.21] : 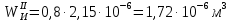 7 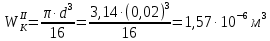 с учетом ослабления пазами для двух стандартных шпонок (табл. 3 приложения методических указаний) [1, с.21] : 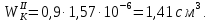 Вычисляем номинальные напряжения: 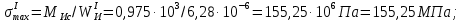 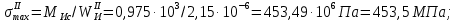 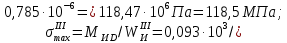 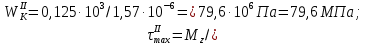 Вычисляем амплитуды и средние напряжения цикла: I. 𝜎а = 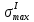 = = 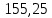 МПа; 𝜎𝑚 = 0; МПа; 𝜎𝑚 = 0; II. 𝜎а = 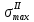 = = 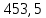 МПа; 𝜎𝑚 = 0; МПа; 𝜎𝑚 = 0; 𝜏𝑚 = 𝜏𝑎 = 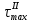 /2 = 39,8 МПа. /2 = 39,8 МПа. III. 𝜎а = 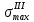 = = 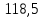 МПа; 𝜎𝑚 = 0. МПа; 𝜎𝑚 = 0.Определяем радиусы галтелей: 𝜌 1 = (𝑑 𝐼 − 𝑑 𝐼I )/2 = (40 − 28)/2 = 6 мм; 𝜌 2 = (𝑑 𝐼𝐼 − 𝑑 𝐼𝐼𝐼)/2 = (28 − 20)/2 = 4 мм. Определяем коэффициенты концентрации напряжений. При 𝜌1 /𝑑𝐼 = 6/40 =0,15 и 𝑑𝐼/𝑑𝐼I= 2 по графику на рисунке 3 имеем (К𝜎 )0 =1,4 [1,c.14]. При 𝜌2 /𝑑𝐼𝐼𝐼 = 4/20 = 0,2 и 𝑑𝐼𝐼/𝑑𝐼𝐼𝐼= 2 по графику на рисунке 3 имеем (К𝜎 )0 = 1,3 [1,c.14]. 8 Учитывая, что в нашем случае D/d = 𝑑𝐼/𝑑𝐼I=1,43 и 𝑑𝐼I/𝑑𝐼II =1,4, используя график на рис. 4, находим поправочные коэффициенты =0,9 (для изгиба, участок I) =0,9 (для изгиба, участок III) [1, c.15]. Находим эффективные коэффициенты концентрации напряжений по формулам: 𝐾𝜎 = 1 +[(𝐾𝜎 )0 − 1], 𝐾𝜏 = 1 +[(𝐾𝜏 )0 − 1], где (𝐾𝜎 )0 и (𝐾𝜏 )0 — эффективные коэффициенты концентрации, соответствующие отношению D/d = 2. 𝐾𝜎 = 1 + 0,9(1,4 – 1) = 1,36. 𝐾𝜏 = 1,7. 𝐾𝜎 = 1,8 (табл. 3, приложение) [1, c.15]. 𝐾𝜎 = 1 + 0,9(1,3 – 1) = 1,27. Коэффициенты влияния абсолютных размеров для вала. dI = 40 мм по рис. 5 (кривая 2) Кd = 0,8. dII = 28 мм по рис. 5 (кривая 2) Кd = 0,85. Приближенно принимаем Кdτ = Кd = 0,85. dIII = 20 мм по рис. 5 (кривая 2) Кd = 0,90[1, c.16]. На поверхности вала наличие окалины, поэтому KF= 0,78 [1, c.22]. Определяем коэффициент чувствительности материала к асимметрии цикла 𝜏 по таблице 2 приложения [1, c.21]. Для стали 40ХН σв = 1000 МПа, тогда 𝜏 = 0,07. Вычисляем коэффициенты запаса прочности: По пределу выносливости: 𝑛𝜎 = 𝜎−1 / (𝐾𝜎  𝜎𝑎/(𝐾𝑑 𝜎𝑎/(𝐾𝑑 𝐾𝐹 )+ 𝜎 𝐾𝐹 )+ 𝜎 𝜎𝑚) . 𝜎𝑚) . 𝑛𝜏 = 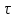 −1 / (𝐾𝜏 −1 / (𝐾𝜏  𝜏𝑎/(𝐾𝑑𝜏 𝜏𝑎/(𝐾𝑑𝜏 𝐾𝐹 ) + 𝜏 𝐾𝐹 ) + 𝜏 𝜏𝑚) . 𝜏𝑚) . I. 𝑛𝜎 = 400/ (( 1,36 · 155,25)/(0,8 · 0,78) + 0) =1,18. II. 𝑛𝜎 = 400 / ((1,8 ·453,5)/(0,85 · 0,78) + 0) = 0,3. 9 𝑛𝜏 = 240/ ((1,7 · 39,8)/(0,85 · 0,78) + 0,04 · 39,8 = 3,86 𝑛 = 𝑛𝜎𝑛𝜏 / √𝑛𝜎2 + 𝑛𝜏2 = 0,3· 3,86/√0,32+3,862 = 0,3. III. 𝑛𝜎 = 400/((1,27 · 118,5)/(0,90 · 0,78)) + 0 = 1,85. По пределу текучести: 𝑛𝜎 = 𝜎т⁄𝜎𝑚𝑎𝑥. 𝑛𝜏 = 𝜏т⁄𝜎𝑚𝑎𝑥. I. 𝑛𝜎 = 800⁄155,25 = 5,15 II. 𝑛𝜎 = 800⁄453,5 = 1,76; 𝑛𝜏 = 390⁄79,6 = 4,9. 𝑛 = 𝑛𝜎𝑛𝜏 √𝑛𝜎 2 + 𝑛𝜏 2 = 1,76 · 4,9/ √1,762+4,92 = 1,66. III. 𝑛𝜎 = 800 ⁄ 118,5 = 6,75. Запасы прочности по пределу выносливости сравним с нормативным коэффициентом запаса прочности [n] = 1,8. Фактические запасы прочности значительно меньше нормативного, поэтому необходимо или увеличить диаметры ступеней вала, определив их из расчета на выносливость, или применить более прочную сталь. 10 Вывод Как показывает анализ причин отказов технических систем, более чем в 70% случаев, разрушения связаны с усталостным повреждением элементов машин, оборудования и сооружений [3]. Такое положение объясняют спецификой явления многоцикловой усталости, в частности: - зарождением и развитием трещин при относительно низких напряжениях; - чувствительностью к различным конструкторским, технологическим факторам; - значительным рассеянием характеристик выносливости по сравнению с характеристиками статической прочности; - локальным и избирательным характером зарождения трещин и их развитием без проявления видимых остаточных перемещений вплоть до момента возникновения аварийных ситуаций. Поэтому актуальной становится проблема предотвращения усталостных разрушений ответственных деталей. 11 Список литературы. 1. МЕТОДИЧЕСКИЕ УКАЗАНИЯ к выполнению курсовой работы по дисциплине «Сопротивление материалов», Пермь, 2017. 2. Гафаров Р.Х., Жернаков В.С. Что нужно знать о сопротивлении материалов: Учеб. Пособие. — М.: Машиностроение, 2001. — 276 с. 3. Александров А.В., Потапов В.Д., Державин Б.П. Сопротивление материалов. — 3е изд. испр. — М.: Высш. шк., 2003. — 560 с. 12 |
