курсовая. КП Лысяникова. Технологический расчет магистрального нефтепровода
 Скачать 2.79 Mb. Скачать 2.79 Mb.
|
|
5 Проверка нефтепровода на прочность, деформацию и общую устойчивость Подземные и наземные (в насыпи) трубопроводы проверяют на прочность, деформацию и общую устойчивость в продольном направлении. Проверку на прочность подземных и наземных (в насыпи) трубопроводов в продольном направлении производят по условию: 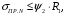 (17) (17)где 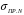 – продольное осевое напряжение от расчетных нагрузок и воздействий, МПа; – продольное осевое напряжение от расчетных нагрузок и воздействий, МПа;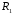 – то же, что и в формуле (10); – то же, что и в формуле (10);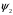 – коэффициент, учитывающий двухосное напряженное состояние металла труб, определяемый по формуле – коэффициент, учитывающий двухосное напряженное состояние металла труб, определяемый по формуле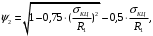 (18) (18)где 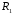 – то же, что и в формуле (10); – то же, что и в формуле (10);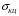 – кольцевые напряжения от расчетного внутреннего давления, МПа, определяются по формуле – кольцевые напряжения от расчетного внутреннего давления, МПа, определяются по формуле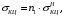 (19) (19)где 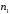 – то же, что и в формуле (9); – то же, что и в формуле (9);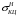 – кольцевые напряжения от рабочего давления, МПа, определяются по формуле – кольцевые напряжения от рабочего давления, МПа, определяются по формуле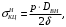 (20) (20)где 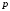 – то же, что и в формуле (9); – то же, что и в формуле (9);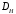 – то же, что и в формуле (9); – то же, что и в формуле (9);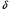 – то же, что и в формуле (16). – то же, что и в формуле (16).Подставив значения в формулу (20), получаем 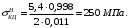 Подставив значения в формулу (19), получаем 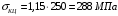 Подставив значения в формулу (18), получаем 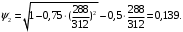 Произведем проверку нефтепровода на прочность по условию, подставив значения в формулу (28), получаем 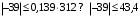 . .Условие выполняется. Проверку на отсутствие недопустимых пластических деформаций подземных и наземных (в насыпи) трубопроводов производят по условиям 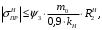 (21) (21)где 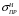 – максимальные суммарные продольные напряжения в трубопроводе от нормативных нагрузок и воздействий, МПа; – максимальные суммарные продольные напряжения в трубопроводе от нормативных нагрузок и воздействий, МПа;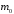 – то же, что и в формуле (10); – то же, что и в формуле (10);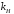 – то же, что и в формуле (10); – то же, что и в формуле (10);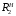 – нормативное сопротивление, которое равно пределу текучести – нормативное сопротивление, которое равно пределу текучести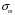 , для нашей марки стали принимаем , для нашей марки стали принимаем 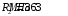 ; ;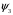 – коэффициент, учитывающий двухосное напряженное состояние металла труб, определяется по формуле – коэффициент, учитывающий двухосное напряженное состояние металла труб, определяется по формуле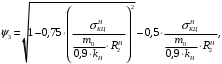 (22) (22)где 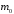 – то же, что и в формуле (10); – то же, что и в формуле (10);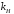 – то же, что и в формуле (10); – то же, что и в формуле (10);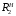 – то же, что и в формуле (21); – то же, что и в формуле (21);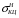 – концевые напряжения, определяющиеся по формулев – концевые напряжения, определяющиеся по формулев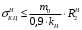 (23) (23)где 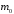 – то же, что и в формуле (10); – то же, что и в формуле (10);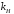 – то же, что и в формуле (10); – то же, что и в формуле (10);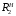 – то же, что и в формуле (21); – то же, что и в формуле (21);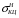 – то же, что и в формуле (20). – то же, что и в формуле (20).Подставив значения в формулу (22), получаем 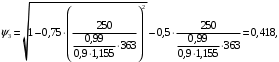 Максимальные суммарные продольные напряжения в трубопроводе от нормативных нагрузок и воздействий определяются по формуле 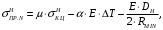 (24) (24)где 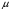 – то же, что и в формуле (23); – то же, что и в формуле (23);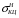 – то же, что и в формуле (20); – то же, что и в формуле (20);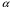 – то же, что и в формуле (12); – то же, что и в формуле (12);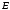 – то же, что и в формуле (12); – то же, что и в формуле (12);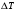 – то же, что и в формуле (13); – то же, что и в формуле (13);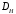 – то же, что и в формуле (11); – то же, что и в формуле (11);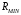 – минимально допустимый радиус упругого изгиба нефтепровода определяется из условий прочности поперечных сварных швов и упругой работы металла труб по формуле – минимально допустимый радиус упругого изгиба нефтепровода определяется из условий прочности поперечных сварных швов и упругой работы металла труб по формуле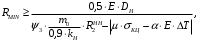 (25) (25)где 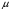 – то же, что и в формуле (23); – то же, что и в формуле (23);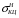 – то же, что и в формуле (20); – то же, что и в формуле (20);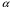 – то же, что и в формуле (12); – то же, что и в формуле (12);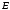 – то же, что и в формуле (12); – то же, что и в формуле (12);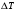 – то же, что и в формуле (3); – то же, что и в формуле (3);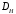 – то же, что и в формуле (11); – то же, что и в формуле (11);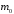 – то же, что и в формуле (10); – то же, что и в формуле (10);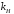 – то же, что и в формуле (10); – то же, что и в формуле (10);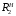 – то же, что и в формуле (21); – то же, что и в формуле (21);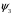 – то же, что и в формуле (22). – то же, что и в формуле (22).Подставив значения в формулу (25), получаем 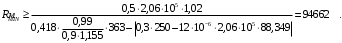 Подставив значения в формулу (24), получаем 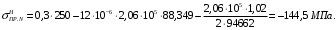 Произведем проверку нефтепровода на отсутствие недопустимых пластических деформаций по условиям. Подставив значения в формулу (23), получаем 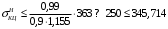 . .Подставив значения в формулу (21), получаем 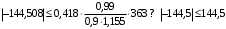 . .Так как неравенства выполняются, делаем вывод о том, что недопустимые пластические деформации нефтепровода отсутствуют. Проверку общей устойчивости трубопровода в продольном направлении в плоскости наименьшей жесткости системы производят по неравенству 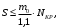 (26) (26)где 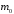 – то же, что и в формуле (10); – то же, что и в формуле (10);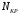 – продольное критическое усилие для прямолинейных участков, Н. – продольное критическое усилие для прямолинейных участков, Н.Находим площадь поперечного сечения металла трубы и осевой момент инерции: 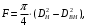 (27) (27)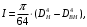 (28) (28)где 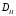 – то же, что и в формуле (11); – то же, что и в формуле (11);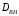 то же, что и в формуле (20). то же, что и в формуле (20).Подставив значения в формулу (27), получаем 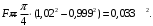 Подставив значения в формулу (28), получаем 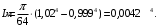 Нагрузка от собственного веса металла трубы рассчитывается по формуле 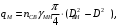 (29) (29)где 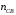 – коэффициент надежности по нагрузкам от действия собственного веса (при расчете на продольную устойчивость – коэффициент надежности по нагрузкам от действия собственного веса (при расчете на продольную устойчивость 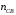 =0,95); =0,95);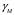 – удельный вес металла, из которого изготовлена труба, для стали – удельный вес металла, из которого изготовлена труба, для стали 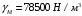 ; ;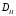 – то же, что и в формуле (11); – то же, что и в формуле (11);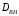 то же, что и в формуле (20). то же, что и в формуле (20).Подставив значения в формулу (29), получаем 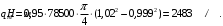 Нагрузку от собственного веса изоляции принимаем равной 10% от 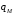 , т.е. , т.е. 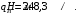 Нагрузка от веса нефти, находящегося в трубопроводе единичной длины, рассчитывается по формуле 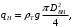 (30) (30)где 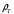 – то же, что и в формуле (1); – то же, что и в формуле (1);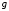 – то же, что и в формуле (8); – то же, что и в формуле (8);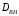 – то же, что и в формуле (20). – то же, что и в формуле (20).Подставив значения в формулу (30), получаем 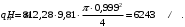 То есть нагрузка от собственного веса заизолированного трубопровода с перекачиваемым нефтепродуктом 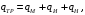 (31) (31)где 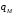 – то же, что и в формуле (29); – то же, что и в формуле (29);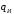 – нагрузку от собственного веса изоляции, Н / м; – нагрузку от собственного веса изоляции, Н / м;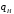 – то же, что и в формуле (30). – то же, что и в формуле (30).Подставив значения в формулу (31), получаем 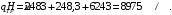 Предположим, что наш трубопровод уложен в песок. Для песка коэффициент сцепления 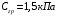 , угол внутреннего трения грунта , угол внутреннего трения грунта 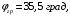 удельный вес песка удельный вес песка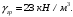 Среднее удельное давление на единицу поверхности контакта трубопровода с грунтом: 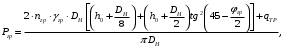 (32) (32)где 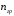 – коэффициент надежности по нагрузке от веса грунта, nгр= 0,8; – коэффициент надежности по нагрузке от веса грунта, nгр= 0,8;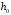 – высота слоя засыпки от верхней образующей трубопровода до поверхности грунта, – высота слоя засыпки от верхней образующей трубопровода до поверхности грунта, 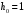 ; ;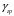 – удельный вес песка, – удельный вес песка, 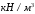 ; ;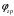 – угол внутреннего трения грунта – угол внутреннего трения грунта 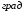 ; ;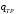 – то же, что и в формуле (31); – то же, что и в формуле (31);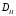 – то же, что и в формуле (11). – то же, что и в формуле (11).Подставив значения в формулу (32), получаем 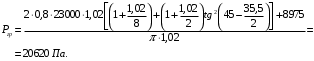 Сопротивление грунта продольным перемещениям отрезка трубопровода единичной длины рассчитывается по формуле 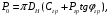 (33) (33)где 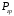 – то же, что и в формуле (32); – то же, что и в формуле (32);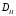 – то же, что и в формуле (11); – то же, что и в формуле (11);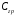 – коэффициент сцепления, – коэффициент сцепления, 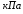 ; ;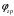 – то же, что и в формуле (32). – то же, что и в формуле (32).Подставив значения в формулу (33), получаем 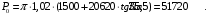 Сопротивление вертикальным перемещениям отрезка трубопровода единичной длины рассчитывается по формуле 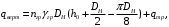 (34) (34)где 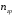 – то же, что и в формуле (32); – то же, что и в формуле (32);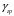 – то же, что и в формуле (32); – то же, что и в формуле (32);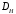 – то же, что и в формуле (11); – то же, что и в формуле (11);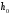 – то же, что и в формуле (32); – то же, что и в формуле (32);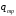 – то же, что и в формуле (31). – то же, что и в формуле (31).Подставив значения в формулу (34), получаем 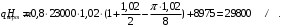 Продольное критическое усилие для прямолинейных участков в случае пластической связи трубы с грунтом находим по формуле 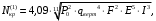 (35) (35)где 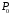 – то же, что и в формуле (33); – то же, что и в формуле (33);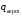 – то же, что и в формуле (32); – то же, что и в формуле (32);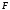 – то же, что и в формуле (38); – то же, что и в формуле (38);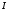 – то же, что и в формуле (39). – то же, что и в формуле (39).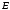 – то же, что и в формуле (12). – то же, что и в формуле (12).Подставив значения в формулу (35), получаем 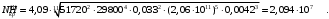 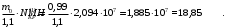 Продольное критическое усилие для прямолинейных участков в случае упругой связи с грунтом рассчитываем по формуле 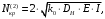 (36) (36)где k0 – коэффициент нормального сопротивления грунта, или коэффициент постели грунта при сжатии; 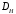 – то же, что и в формуле (11); – то же, что и в формуле (11);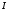 – то же, что и в формуле (39); – то же, что и в формуле (39);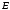 – то же, что и в формуле (24). – то же, что и в формуле (24).Подставив значения в формулу (36), получаем 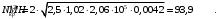 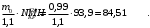 Фактическое эквивалентное продольное усилие в сечении трубы рассчитывается по формуле 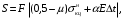 (37) (37)где 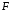 – то же, что и в формуле (27); – то же, что и в формуле (27);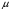 – то же, что и в формуле (12); – то же, что и в формуле (12);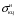 – то же, что и в формуле (20); – то же, что и в формуле (20);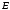 – то же, что и в формуле (12); – то же, что и в формуле (12);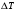 – то же, что и в формуле (13). – то же, что и в формуле (13).Подставив значения в формулу (37), получаем 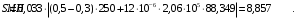 Так как по условию, 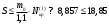 и и 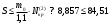 , то общая устойчивость прямолинейных участков нефтепровода обеспечена. , то общая устойчивость прямолинейных участков нефтепровода обеспечена. Теперь проверим общую устойчивость криволинейных участков трубопроводов, выполненных с упругим изгибом. Определим параметры и z по формулам 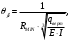 (38) (38)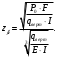 (39) (39)где 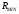 – то же, что и в формуле (25); – то же, что и в формуле (25);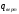 – то же, что и в формуле (34); – то же, что и в формуле (34);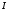 – то же, что и в формуле (28); – то же, что и в формуле (28);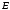 – то же, что и в формуле (12); – то же, что и в формуле (12);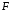 – то же, что и в формуле (27); – то же, что и в формуле (27);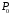 – то же, что и в формуле (33). – то же, что и в формуле (33).Подставив значения в формулу (38), получаем 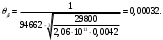 Подставив значения в формулу (39), получаем 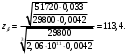 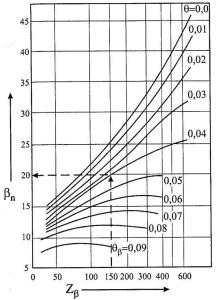 Рисунок 1 – Номограмма для определения коэффициента βN По графику находим, что N 23. Вычисляем критическое усилие для криволинейных участков трубопровода: 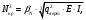 (40) (40)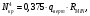 (41) (41)где 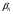 – коэффициент; – коэффициент;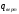 – то же, что и в формуле (34); – то же, что и в формуле (34);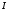 – то же, что и в формуле (28); – то же, что и в формуле (28);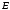 – то же, что и в формуле (12); – то же, что и в формуле (12);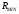 – то же, что и в формуле (25). – то же, что и в формуле (25).Подставив значения в формулу (40), получаем 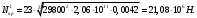 Подставив значения в формулу (41), получаем 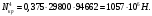 Из двух найденных значений выбираем меньшее и для него 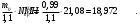 Так как, 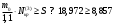 , то условие устойчивости криволинейных участков выполняется. , то условие устойчивости криволинейных участков выполняется.В таблице 6 представлены результаты проверки нефтепровода на прочность, деформацию и общую устойчивость Таблица 6 – Проверка нефтепровода на прочность, деформацию и общую устойчивость
Продолжение таблицы 6
|

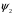 (18)
(18)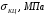 (19)
(19)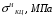 (20)
(20)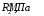
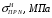 (24)
(24)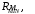 (25)
(25)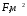 (27)
(27)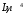 (28)
(28)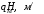 (29)
(29)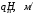
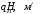 (30)
(30)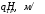 (31)
(31)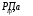 (32)
(32)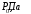 (33)
(33)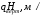 (34)
(34)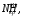 (35)
(35)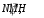 (36)
(36)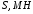 (37)
(37)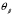 (38)
(38)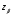 (39)
(39)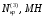 (40)
(40)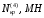 (41)
(41)