лабораторная работа. №7 лабораторная МП. Технология решения обыкновенных дифференциальных уравнений

• Название: Технология решения обыкновенных дифференциальных уравнений
• Анкор: лабораторная работа
• Дата: 21.10.2022
• Размер: 34.83 Kb.
• Имя файла: №7 лабораторная МП.docx
• Тип: Лабораторная работа; #747033

Федеральное агентство связи Ордена

Трудового Красного Знамени

федеральное бюджетное образовательное учреждение высшего образования

«Московский Технический Университет Связи и Информатики»

(МТУСИ)

Кафедра Информатики

Предмет: Введение в математические пакеты прикладных программ

Лабораторная работа по ВвМППП № 7

Тема:

“ Технология решения обыкновенных
дифференциальных уравнений”

Вариант 00

Выполнил:

Великий преподователь
__________________________

Москва 0000

1.Общее задание

1. 
   Изучите материал Темы 2.4 (п. 2.4.1).
   
2. 
   Выберите индивидуальный вариант задания из табл. 2.4.2-1.
   
3. 
   Вычислить значение производной от функции f(x) в произвольной точке с использованием функции numderivative();
   
4. 
   Найдите решение ОДУ на отрезке [a;b] с шагом h с использованием функции ode() .
   
5. 
   Создайте матрицу решений, записав в первый столбец аргумент, а во второй - решение, полученное с использованием функций ode().
   
6. 
   Выведите полученную таблицу по столбцам.
   
7. 
   Постройте график полученных решений ОДУ.
   
8. 
   Сохраните текст рабочего окна на внешнем носителе.
   
9. 
   Предоставьте результаты работы преподавателю, ответьте на поставленные вопросы.
   
10. 
    Оформите отчет по выполненной работе.
    

Индивидуальное задание:

//Лабораторная работа №7 по теме:"Технология решения обыкновенных дифференциальных уравнений средставами Scilab"

// Выполнил:

//Вариант №--

//Описание функции f(x)

deff('y=f(x)','y=2^x+log(2.*x)-5.6*x.^4')

// Вычисление производной в произвольной точке x=7

numderivative(f,7)

ans =

-7594.3343

//Проверка результатов дифференциирования

deff('y1=f1(x)','y1=log(2)*2^x+1/(2.*x)-22.4*x.^3')

f1(7)

ans =

-7594.4057

//Вычисление решения ОДУ на отрезке [4;0.5]с шагом 0.5

deff('yd=f(t,x)','yd=t*(x-t).^2')

//Задание начальных условий

y0=1;t0=4;t=4:-0.5:0.5;

//Описание функции f(x)

y=ode(y0,t0,t,f);

plot(t,y,'-o')

xgrid();

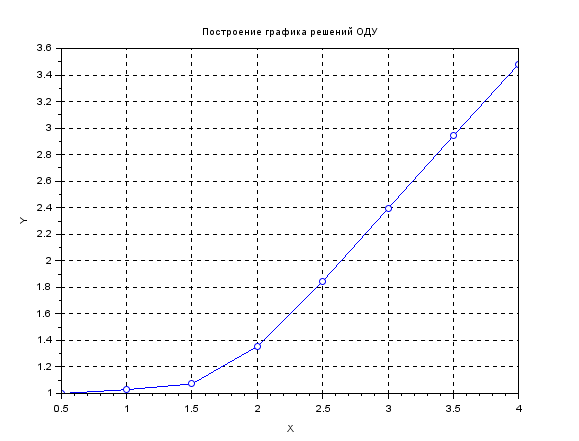
xtitle('Построение графика решений ОДУ','X','Y');

yr=[t;y];//Создание и вывод матрицы решений

yr'

//Построить график полученных решений ОДУ

function yd=f(t,x), yd=t*(x-t).^2, endfunction;

x0=1;t0=0.5;t=0.5:0.5:4;

y=ode(x0,t0,t,f);

plot(t,y,'-o')

xgrid();

yy=[t;y];

yy'

ans =

0.5 1.

1. 1.029071

1.5 1.0720121

2. 1.3550733

2.5 1.8450416

3. 2.3933061

3.5 2.9421516

4. 3.4823058