да12345678910111213. Тема Построение математических моделей для решения практических задач. Архитектура современных компьютеров. Многопроцессорные системы

• Название: Тема Построение математических моделей для решения практических задач. Архитектура современных компьютеров. Многопроцессорные системы
• Анкор: да12345678910111213
• Дата: 21.04.2023
• Размер: 0.76 Mb.
• Имя файла: ege22.doc
• Тип: Документы; #1079187
• страница: 1 из 5

© К. Поляков, 2022

22 (повышенный уровень, время – 7 мин)

Тема: Построение математических моделей для решения практических задач. Архитектура современных компьютеров. Многопроцессорные системы

Что проверяется:

Умение анализировать алгоритм, содержащий ветвление и цикл

3.1.1. Программная и аппаратная организация компьютеров и компьютерных систем. Виды программного обеспечения.

1.3.2. Оценивать скорость передачи и обработки информации.

Что нужно знать:

• 
  процессы в современных компьютерах могут выполняться параллельно, если являются независимыми
  
• 
  выражение «процесс В зависит от процесса А» означает, что выполнение процесса В не может начаться раньше, чем выполнение процесса А
  

Пример задания:

P-00 (демо-2022). В файле 22-0.xls содержится информация о совокупности N вычислительных процессов, которые могут выполняться параллельно или последовательно. Будем говорить, что процесс B зависит от процесса A, если для выполнения процесса B необходимы результаты выполнения процесса A. В этом случае процессы могут выполняться только последовательно. Информация о процессах представлена в файле в виде таблицы. В первом столбце таблицы указан идентификатор процесса (ID), во втором столбце таблицы – время его выполнения в миллисекундах, в третьем столбце перечислены с разделителем «;» ID процессов, от которых зависит данный процесс. Если процесс является независимым, то в таблице указано значение 0.

Определите минимальное время, через которое завершится выполнение всей совокупности процессов, при условии, что все независимые друг от друга процессы могут выполняться параллельно.

Типовой пример организации данных в файле:

ID процесса B	Время выполнения процесса B (мс)	ID процесса(ов) A
1	4	0
2	3	0
3	1	1; 2
4	7	3

В данном случае независимые процессы 1 и 2 могут выполняться параллельно, при этом процесс 1 завершится через 4 мс, а процесс 2 – через 3 мс с момента старта. Процесс 3 может начаться только после завершения обоих процессов 1 и 2, то есть, через 4 мс после старта. Он длится 1 мс и закончится через 4 + 1 = 5 мс после старта. Выполнение процесса 4 может начаться только после завершения процесса 3, то есть, через 5 мс. Он длится 7 мс, так что минимальное время завершения всех процессов равно 5 + 7 = 12 мс.

Решение (электронные таблицы):

1. 
   таблица имеет вид:
   

   ID процесса B	Время выполнения процесса B (мс)	ID процесса (ов) A
   1	4	0
   2	3	0
   3	1	1; 2
   4	7	3
   5	6	3
   6	3	5
   7	1	4; 6
   8	2	7
   9	7	0
   10	8	0
   11	6	9
   12	6	10

2. 
   отсортируем данные в таблице так, чтобы:
   

– все независимые процессы оказались в начале таблицы

– любой процесс был расположен ПОСЛЕ всех процессов, от которых он зависит

ID процесса B	Время выполнения процесса B (мс)	ID процесса (ов) A
1	4	0
2	3	0
9	7	0
10	8	0
3	1	1; 2
4	7	3
5	6	3
6	3	5
7	1	4; 6
8	2	7
11	6	9
12	6	10

3. 
   добавляем еще один столбец: время окончания процесса; для всех независимых процессов записываем в соответствующие ячейки время окончания, равное длительности процесса:
   

   ID процесса B	Время выполнения процесса B (мс)	ID процесса (ов) A	Время окончания T, мс
   1	4	0	4
   2	3	0	3
   9	7	0	7
   10	8	0	8
   3	1	1; 2
   4	7	3
   5	6	3
   6	3	5
   7	1	4; 6
   8	2	7
   11	6	9
   12	6	10

4. 
   для остальных процессов определяем время окончания как сумму длительности этого процесса и максимального времени окончания процессов, от которых зависит данный процесс (здесь T(x) обозначает время окончания процесса с идентификатором x):
   

T(3) = 1 + max( T(1), T(2) ) = 1 + 4 = 5

T(4) = 7 + T(3) = 7 + 5 = 12

T(5) = 6 + T(3) = 6 + 5 = 11

T(6) = 3 + T(5) = 3 + 11 = 14

T(7) = 1 + max( T(4), T(6) ) = 1 + 14 = 15

T(8) = 2 + T(7) = 2 + 15 = 17

T(11) = 6 + T(9) = 6 + 7 = 13

T(12) = 6 + T(10) = 6 + 8 = 14

ID процесса B	Время выполнения процесса B (мс)	ID процесса (ов) A	Время окончания T, мс
1	4	0	4
2	3	0	3
9	7	0	7
10	8	0	8
3	1	1; 2	5
4	7	3	12
5	6	3	11
6	3	5	14
7	1	4; 6	15
8	2	7	17
11	6	9	13
12	6	10	14

5. 
   время завершения совокупности всех процессов равно времени завершения последнего из них, поэтому нужно выбрать максимальное значение в последнем столбце
   
6. 
   Ответ: 17.
   

Решение (электронные таблицы, функция ВПР, Информатик БУ):

1. 
   Для начала отсортируем таблицу по столбцу C (ID процесса (ов) A). Это нужно для того, чтобы отдельно рассмотреть независимые процессы (те, у которых в столбце C находится значение 0); вместо этого можно было бы использовать функцию ЕСЛИ, но в этом случае формула была бы немного сложнее;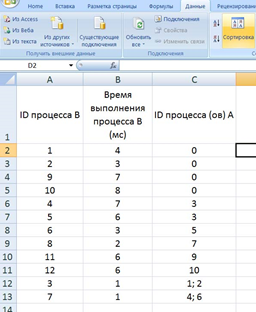
   

2. 
   Теперь необходимо расцепить процессы в ячейках столбца C, в которых находится более одного процесса; в данном примере это можно было бы сделать вручную, но ручной способ не подойдет для больших таблиц. Для этого выделяем нужные ячейки столбца C, переходим в меню «Данные», и нажимаем кнопку «Текст по столбцам»:
   

В появившемся окне выбираем формат данных «с разделителями», нажимаем кнопку «Далее», и указываем символы, которые разделяют процессы в ячейках. В нашем случае это точка с запятой и пробел. Нажимаем кнопку «Готово».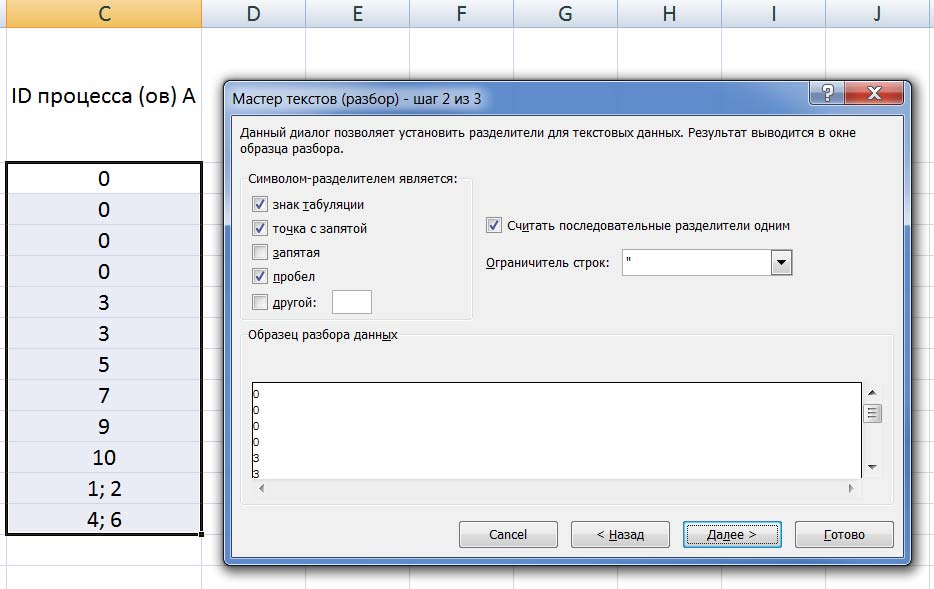



После этого один из процессов останется в столбце C, а второй отправится в столбец D (если процессов больше, чем 2, номера оставшихся размещаются в столбцах E, F и далее).

3. 
   Посчитаем в столбце E полное время выполнения каждого процесса (время самого процесса + время процессов, связанных с ним). Сначала отдельно рассмотрим независимые процессы. Для этого в ячейке E2 пишем формулу =B2, и копируем её для всех независимых процессов.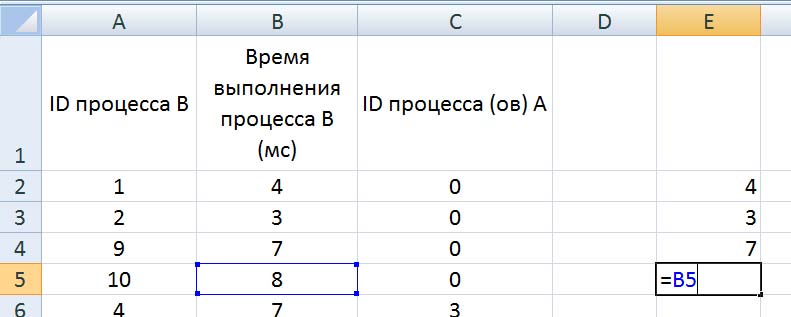
   

4. 
   Теперь рассмотрим процессы B, которые зависят только от одного процесса. Для этого возьмем время выполнения самого процесса B, и прибавим к нему полное время выполнения процесса A (ID процесса A находится в столбце C, а полное время выполнения – в столбце E). Для поиска времени выполнения процесса A воспользуемся функцией ВПР. В ячейку E6 запишем формулу:
   

=B6+ВПР(C6;A:E;5;0)

и скопируем её для всех процессов B, у которых указан только один процесс A.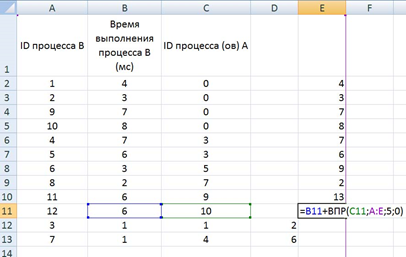

5. 
   Далее рассмотрим процессы B, которые зависят уже от двух процессов. Так как процессы в столбцах C и D могут выполняться параллельно, будем брать максимальное значение среди времени их выполнения, и прибавлять к этому значению время выполнения самого процесса B. Для этого в ячейку E12 запишем формулу:
   

=B12+МАКС(ВПР(C12;A:E;5;0);ВПР(D12;A:E;5;0))

и копируем её для всех процессов B, у которых указано два процесса A.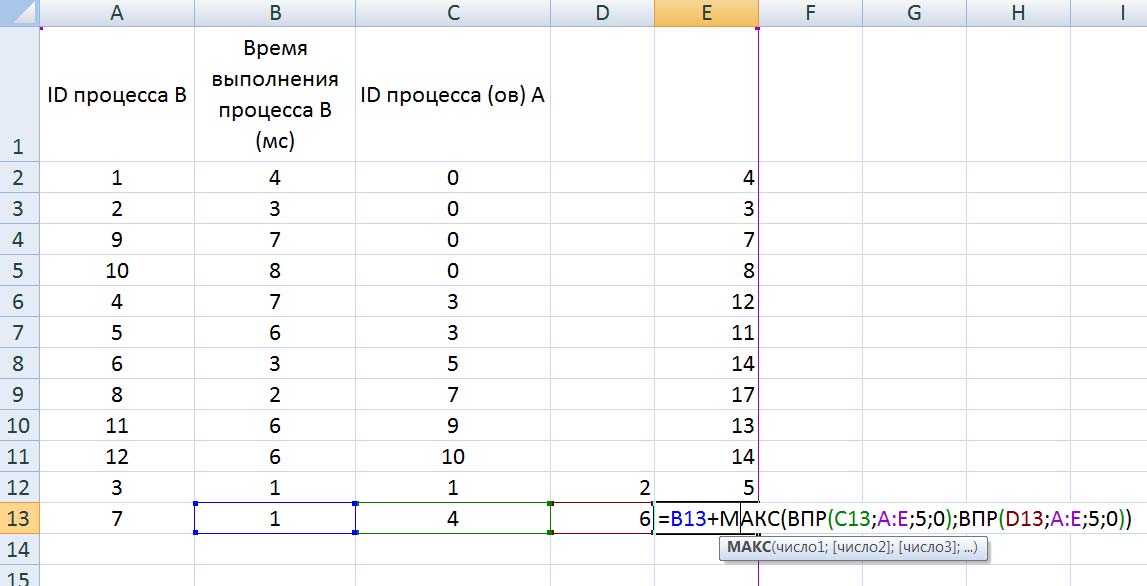

6. 
   Так мы получили столбец E, в ячейках которого указано полное время выполнения каждого процесса B. Так как процессы могут выполняться параллельно, нам остаётся найти максимальное значение в ячейках столбца E. Для этого в любую пустую ячейку пишем формулу: =МАКС(A:A) и получаем ответ: 17.
   
7. 
   Ответ: 17.
   

Решение (электронная таблица, С. Кох):

1. 
   сортируем таблицу по первому столбцу (ID процесса B) и добавляем первой строкой (в электронной таблице – в строку 2) фиктивный процесс в которую записываем процесс с ID = 0, время выполнения 0 и время окончания процесса 0: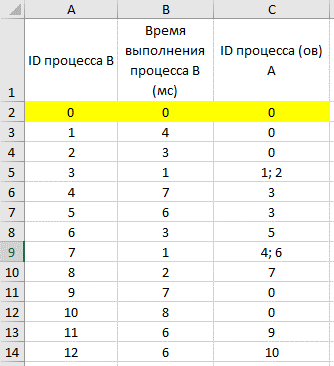
   

2. 
   расцепляем процессы в ячейках столбца C с помощью функции «Текст по столбцам» (см. выше в решении Информатика БУ):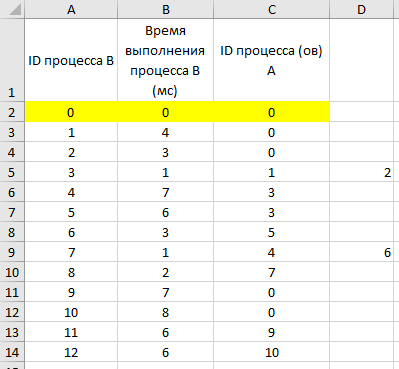
   

3. 
   В первом свободном столбце в 3-й строке пишем формулу, которая учитывает максимальное количество процессов, которое встречается в этой задаче (например, здесь в E3 пишем формулу =МАКС(ВПР(C3;A:E;5);ВПР(D3;A:E;5))+B3)
   

и растягиваем эту формулу на весь столбец. В этом случае все пустые ячейки Excel считает равными 0 и обращается к 0 процессу, время завершения которого 0.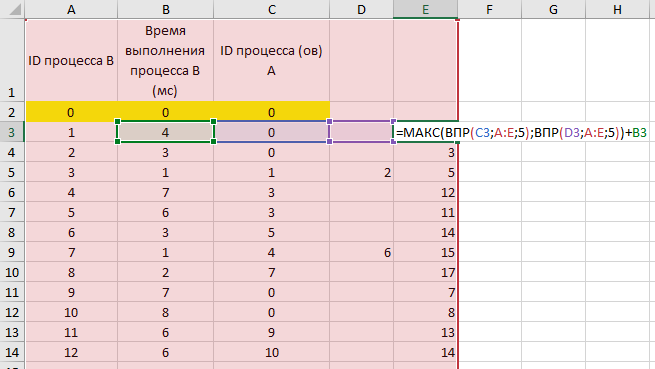

4. 
   находим максимум в последнем столбце: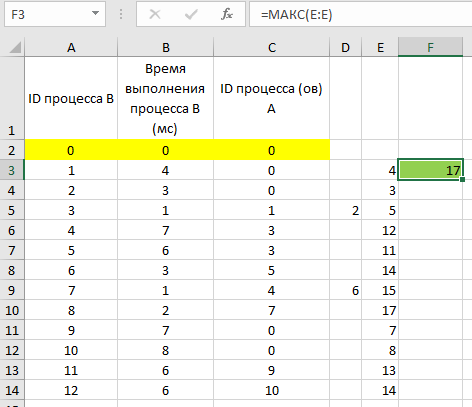
   

5. 
   Ответ: 17.
   

Решение (диаграмма Ганта, А. Кожевникова):

1. 
   Решение удобно выполнять в Excel, построив диаграмму Ганта, которая показывает зависимость процессов. Построение диаграммы состоит в закрашивании ячеек таблицы Excel разным цветом, длина (количество закрашиваемых ячеек) процесса соответствует времени его выполнения.
   
2. 
   Построим диаграмму Ганта для таблицы, приведённой в задании:
   

   ID процесса B	Время выполнения процесса B (мс)	ID процесса (ов) A
   1	4	0
   2	3	0
   3	1	1; 2
   4	7	3
   5	6	3
   6	3	5
   7	1	4; 6
   8	2	7
   9	7	0
   10	8	0
   11	6	9
   12	6	10

3. 
   Сначала отобразим на диаграмме процесс 1 и 2. Оба процесса начинаются независимо друг от друга. Поэтому строим оба процесса с самого начала.
   

   1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18
   1
   2

4. 
   процесс 3 длительностью 1 начинается только после окончания процессов 1 и 2:
   

   1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18
   1				3
   2

5. 
   Процессы 4 и 5 начинаются после выполнения процесса 3:
   

   1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18
   1				3	4
   2					5

6. 
   Процесс 6 начинается после выполнения процесса 5. Процесс 7 начинается после завершения процессов 4 и 6. Процесс 8 начинается после завершения процесса 7.
   

   1	2	3	4	5	6	7	8	9	10	11	12		13	14	15	16	17	18
   1				3	4										7	8
   2					5							6

7. 
   Процессы 9 и 10 начинаются сразу в момент 0, так как независимы от других процессов. Процесс 11 начинается после завершения процесса 9, а процесс 12 процесс сразу после завершения процесса 10.
   

   1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18
   1				3	4									7	8
   2					5						6
   9							11
   10								12

8. 
   Позже всех – через 17 мс – заканчивается процесс 8. Это и есть минимальное время завершения всей совокупности процессов.
   
9. 
   Ответ: 17.
   

Решение (программа):

1. 
   можно решить задачу с помощью программы, если сохранить файл в CSV-формате (меню Файл – Сохранить как); файл будет выглядеть так:
   

ID процесса B;Время выполнения процесса B (мс);ID процесса (ов) A;

1;4;0;

2;3;0;

3;1;"1; 2";

4;7;3;

5;6;3;

6;3;5;

7;1;"4; 6";

8;2;7;

9;7;0;

10;8;0;

11;6;9;

12;6;10;

2. 
   для чтения CSV-файла проще всего применить объект reader из стандартного модуля csv:
   

from csv import reader

with open( "22-0.csv", encoding="cp1251" ) as F:

rdr = reader( F, delimiter=';', quotechar='"' ) # (1)

next( rdr ) # читаем заголовки и пропускаем их # (2)

...

параметр encoding, переданный функции open, означает, что файл сохранен в кодировке Windows (CP-1251), именно так сохраняет CSV-файлы Excel; тут проблема только в чтении русских букв, поэтому можно просто заранее удалить из файла первую строку с заголовками

3. 
   в строке (1) создается объект reader, в параметрах указываем, что разделитель данных (delimiter) – точка с запятой, а знак " используется как кавычка (quotechar)
   
4. 
   в строке (2) мы читаем (и не сохраняем) строку с заголовками, если, конечно, не удалили ее заранее; если удалили, то функцию next() вызывать не нужно
   
5. 
   теперь займемся хранением данных; будем использовать два словаря:
   

• 
  словарь finalTime содержит уже известные значения времени окончания процессов (вызов: finalTime[id] даёт время окончания процесса с идентификатором id)
  
• 
  словарь data содержит данные тех процессов, для которых время окончания неизвестно: вызов data[id] даёт кортеж (t, dependsOn), где
  

t – длительность процесса с идентификатором id,

dependsOn – массив идентификаторов процессов, от которых зависит данный процесс

6. 
   в цикле читаем данные из файла;
   

for s in rdr:

id, t = int(s[0]), int(s[1])

dependsOn = list( map( int, s[2].split(';') ) )

if dependsOn == [0]:

finalTime[id] = t # известно время окончания

else:

data[id] = ( t, dependsOn ) # неизвестно время окончания

массив строк s содержит данные одной строки CSV-файла

• 
  s[0] – идентификатор (эту строку нужно преобразовать в целое число, вызвав int)
  
• 
  s[1] – длительность процесса (тоже нужно преобразовать в целое число)
  
• 
  s[2] – перечисление идентификаторов процессов, от которых зависит данный процесс; эта строка может иметь, например, такой вид:
  

'1; 2'

в результате вызова s[2].split(';') получаем такой массив из двух строк

['1', '2']

применяя к каждому элементу функцию int, получаем массив целых чисел dependsOn:

[1, 2]

Если этот массив состоит только из нуля, сразу записываем в словарь finalTime идентификатор и соответствующее ему время окончания процесса, которое равно длительности процесса (считаем, что он стартует в момент 0):

if dependsOn == [0]:

finalTime[id] = t # известно время окончания

else:

data[id] = ( t, dependsOn ) # неизвестно время окончания

Если же у процесса есть зависимости, записываем в словарь data кортеж, в котором хранятся длительность процесса и массив dependsOn идентификаторов процессов, от которых он зависит.

7. 
   самое интересное – это обработка данных словаря data; все эти данные нужно преобразовать в соответствующие элементы словаря finalTime так чтобы словарь data стал пустым; делаем так:
   

while data:

ids = list(data.keys())

for id in ids:

# если известны моменты окончания всех процессов, от

# которых зависит процесс id, записать в finalTime время

# окончания этого процесса и удалить данные процесса id из

# словаря data

8. 
   чтобы определить, что моменты окончания всех нужных процессов известны, используем функцию all:
   

if all( (x in finalTime) for x in dependsOn ):

...

это значит «если все идентификаторы из массива dependsOn уже есть в словаре finalTime»

9. 
   определяем время старта процесса id как максимальное время завершения всех процессов, от которых он зависит:
   

startId = max( finalTime[x] for x in dependsOn )

10. 
    вычисляем время окончания процесса id:
    

finalTime[id] = startId + t

и удаляем данные этого процесса из массива data:

del data[id]

11. 
    вот полный цикл обработки:
    

while data:

ids = list(data.keys())

for id in ids:

t, dependsOn = data[id]

if all( (x in finalTime) for x in dependsOn ):

startId = max( finalTime[x] for x in dependsOn )

finalTime[id] = startId + t

del data[id]

12. 
    ответ – это максимальное время окончания процесса из словаря finalTime:
    

print( "Ответ:", max(finalTime.values()) )

13. 
    полная программа:
    

from csv import reader

with open( "22-0.csv", encoding="cp1251" ) as F:

rdr = reader( F, delimiter=';', quotechar='"' )

next( rdr ) # читаем заголовки и пропускаем их

data = {}

finalTime = {}

for s in rdr:

id, t = int(s[0]), int(s[1])

dependsOn = list( map( int, s[2].split(';') ) )

if dependsOn == [0]:

finalTime[id] = t # известно время окончания

else:

data[id] = ( t, dependsOn ) # неизвестно время окончания

while data:

ids = list(data.keys())

for id in ids:

t, dependsOn = data[id]

if all( (x in finalTime) for x in dependsOn ):

startId = max( finalTime[x] for x in dependsOn )

finalTime[id] = startId + t

del data[id]

print( "Ответ:", max(finalTime.values()) )

14. 
    обратим внимание, что программа не использует никаких предположений о расположении данных о процессах в исходном списке, они могут быть расположены в произвольном порядке
    
15. 
    программа зациклится, если данные будут некорректны, например, процесс 1 зависит от процесса 2, а процесс 2 – от процесса 1 (циклическая ссылка)
    
16. 
    Ответ: 17.