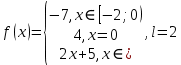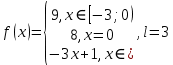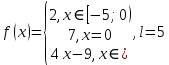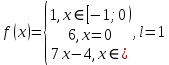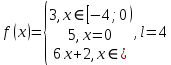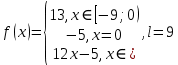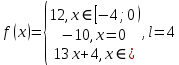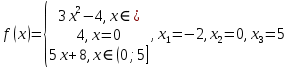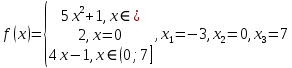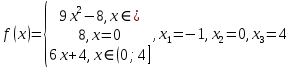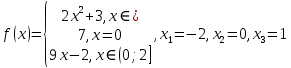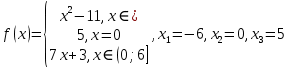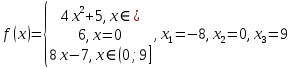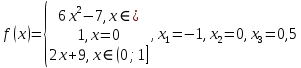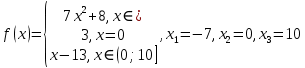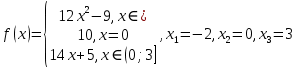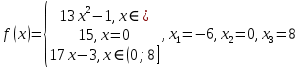Тема 1 Ряды Фурье
 Скачать 30.4 Kb. Скачать 30.4 Kb.
|
Практическое задание 6Тема 4.1 «Ряды Фурье» Задание 6.1. Получить разложение функции 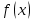 в тригонометрический ряд Фурье на отрезке [ в тригонометрический ряд Фурье на отрезке [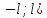 . Выяснить, в каких точках отрезка ряд сходится к функции . Выяснить, в каких точках отрезка ряд сходится к функции 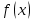 . . Номер варианта взять равным остатку от деления на 10 порядкового номера первой буквы вашей фамилии в алфавите.
Алгоритм выполнения задания 6.1 Вычислите коэффициенты тригонометрического ряда Фурье функции 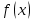 . .Запишите тригонометрический ряд Фурье функции 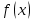 на отрезке [ на отрезке [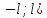 . .С помощью теоремы Дирихле выясните, в каких точках отрезка [ 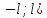 сумма полученного ряда совпадает с функцией сумма полученного ряда совпадает с функцией 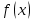 . .Образец выполнения задания 6.1Пусть 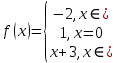 . .Получить разложение данной функции в тригонометрический ряд Фурье на отрезке [ 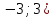 . Выяснить, в каких точках отрезка ряд сходится к функции . Выяснить, в каких точках отрезка ряд сходится к функции 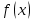 . .Решение. Вычислим коэффициент 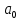 : :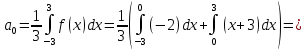 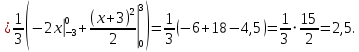 Теперь найдем коэффициенты 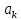 и и 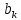 для для 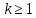 : :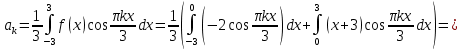 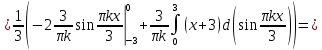 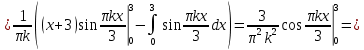 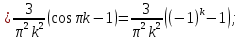 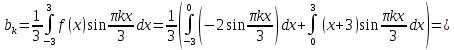 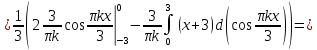 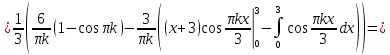 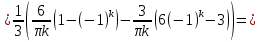 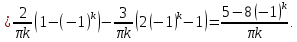 Таким образом, тригонометрический ряд Фурье функции 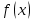 на отрезке [ на отрезке [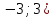 имеет вид имеет вид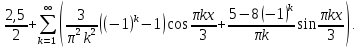 (1) (1)Пусть 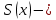 cумма ряда (1). В соответствии с теоремой Дирихле cумма ряда (1). В соответствии с теоремой Дирихле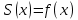 , если , если 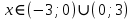 ; ; 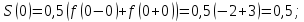 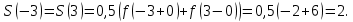 Учитывая, что 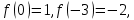 а а 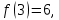 делаем вывод, что в точках 0, −3 и 3 значения функции делаем вывод, что в точках 0, −3 и 3 значения функции 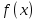 и суммы ее ряда Фурье (1) различаются. и суммы ее ряда Фурье (1) различаются.Задание 6.2. Найти значения суммы тригонометрического ряда Фурье функции 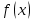 в заданных точках. в заданных точках. Номер варианта взять равным остатку от деления на 10 порядкового номера первой буквы вашей фамилии в алфавите.
Алгоритм выполнения задания 6.2 Для каждой из заданных точек определите, является ли она точкой непрерывности функции 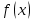 из интервала из интервала 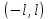 , концевой точкой отрезка [ , концевой точкой отрезка [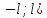 или точкой разрыва функции или точкой разрыва функции 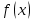 из интервала из интервала 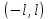 . .Для нахождения значений функции 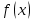 в указанных точках примените теорему Дирихле. в указанных точках примените теорему Дирихле.Образец выполнения задания 6.2Найти значения суммы тригонометрического ряда Фурье функции 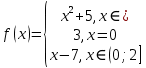 в точках 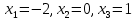 . .Решение. Пусть 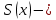 cумма тригонометрического ряда Фурье функции cумма тригонометрического ряда Фурье функции 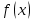 . Поскольку функция . Поскольку функция 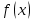 непрерывна во всех точках отрезка непрерывна во всех точках отрезка 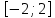 кроме точки кроме точки 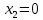 (в точках (в точках 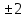 мы имеем в виду одностороннюю непрерывность), то согласно теореме Дирихле мы имеем в виду одностороннюю непрерывность), то согласно теореме Дирихле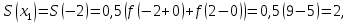 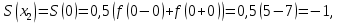 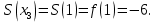 |