Тема 10. Вариант 4. Тема 10. Регрессионный анализ особенности множественной линейные модели

• Название: Тема 10. Регрессионный анализ особенности множественной линейные модели
• Дата: 27.11.2018
• Размер: 38.48 Kb.
• Имя файла: Тема 10. Вариант 4.docx
• Тип: Документы; #57867

Тема №10. «Регрессионный анализ: особенности множественной линейные модели

Задание:

1. Построить матрицу парных и частных коэффициентов корреляции. Сделать вывод о наличии мультиколлинеарности.

2. Ввести в модель фиктивные переменные, провести анализ модели.

3. Дать интерпретацию полученным результатам.
Вариант №4

По выборке из 20 почтовых отправлений изучается зависимость стоимости отправки корреспонденции экспресс почтой от веса конверта и дальности перевозки

26	590	0,5		110	510	2,4
39	320	1,5		50	240	2,1
80	440	2,0		20	30	1,6
92	660	1,6		60	620	1,2
44	75	2,8		11	270	0,4
15	70	0,8		80	350	2,5
145	650	2,4		33	410	1,0
19	450	0,5		121	810	1,6
10	60	1,0		155	700	2,6
140	750	1,9		17	110	0,9

Вспомогательная таблица расчётов:

№	x1	x2	x3	x1x2	x1x3	x2x3	x12	x22	x32
1	26	590	0,5	15340	13	295	676	348100	0,25
2	39	320	1,5	12480	58,5	480	1521	102400	2,25
3	80	440	2,0	35200	160	880	6400	193600	4
4	92	660	1,6	60720	147,2	1056	8464	435600	2,56
5	44	75	2,8	3300	123,2	210	1936	5625	7,84
6	15	70	0,8	1050	12	56	225	4900	0,64
7	145	650	2,4	94250	348	1560	21025	422500	5,76
8	19	450	0,5	8550	9,5	225	361	202500	0,25
9	10	60	1,0	600	10	60	100	3600	1
10	140	750	1,9	105000	266	1425	19600	562500	3,61
11	110	510	2,4	56100	264	1224	12100	260100	5,76
12	50	240	2,1	12000	105	504	2500	57600	4,41
13	20	30	1,6	600	32	48	400	900	2,56
14	60	620	1,2	37200	72	744	3600	384400	1,44
15	11	270	0,4	2970	4,4	108	121	72900	0,16
16	80	350	2,5	28000	200	875	6400	122500	6,25
17	33	410	1,0	13530	33	410	1089	168100	1
18	121	810	1,6	98010	193,6	1296	14641	656100	2,56
19	155	700	2,6	108500	403	1820	24025	490000	6,76
20	17	110	0,9	1870	15,3	99	289	12100	0,81
Сумма:	1267	8115	31,3	695270	2469,7	13375	125473	4506025	59,87

Проведем корреляционный анализ по имеющимся факторам 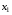, , 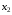, 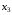над которыми производилась серия из 20 независимых наблюдений. Определим корреляционную (линейную) зависимость между ними и построим матрицу парных коэффициентов корреляции. Для этого воспользуемся формулой выборочного коэффициента корреляции: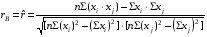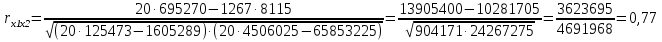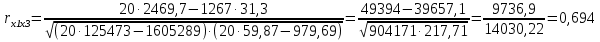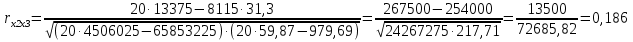

.






Матрица парных коэффициентов корреляции:

	x1	x2	x3
x1	1	0,77	0,694
x2	0,77	1	0,186
x3	0,694	0,186	1

Так как в корреляционной матрице факторных переменных отсутствуют коэффициенты парной корреляции по абсолютной величине большие 0,8, то можно делать вывод о том, что в данной модели множественной регрессии мультиколлинеарность не существует.

Вычислим определитель матрицы парных коэффициентов корреляции: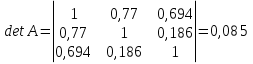



Величина определителя матрицы мала, но достаточна для того, чтобы подтвердить гипотезу об отсутствии мультиколлинеарности.
Для того чтобы исключить эффект влияния других факторов на зависимость между конкретными x_i и x_j находим частную корреляцию: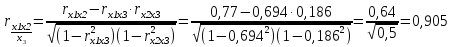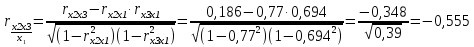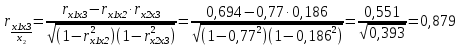






Матрица частных коэффициентов корреляции:

	x1	x2	x3
x1	1	0,905	0,879
x2	0,905	1	-0,555
x3	0,879	-0,555	1

Исходя из полученных данных можно говорить, что между переменными х₂ и х₃ отсутствует линейная связь (что доказывается поставленным условием задачи)
Множественный коэффициент корреляции: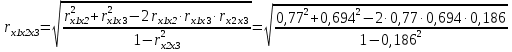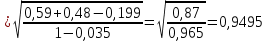





Множественный коэффициент корреляции показывает тесноту линейной связи между всеми переменными в совокупности.