Практическое задание 3. Тема Алгоритмы сортировки
 Скачать 0.57 Mb.
|
 Практическое задание № 3Тема 3.2. Алгоритмы сортировки Цель работы: изучить основные алгоритмы поиска и сортировки; провести сравнительный анализ различных алгоритмов поиска и сортировки. Формулировка задания № 3 Изучить следующие методы сортировки: включение; выбор; обмен; сортировка Шелла; сортировка Хоара; пирамидальная сортировка. Реализовать упомянутые выше методы. Проанализировать время, затрачиваемое на каждый из них при одинаковом количестве измерений (количестве элементов в массиве). Изучить алгоритмы поиска: в неупорядоченном массиве: линейный; быстрый линейный; в упорядоченном массиве: быстрый; бинарный; блочный. 4. Реализовать данные алгоритмы в одном файле в виде отдельных подпрограмм (функций). 5. Проанализировать, на какой итерации при разных алгоритмах поиска было найдено искомое число. Выполнение задания. 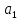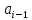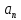Исследование алгоритмов сортировки Сортировка включениями – элементы массива условно разделяются на готовую последовательность  ,  , …,  и входную последовательность  ,  , …, . На каждом шаге i-й элемент помещается на подходящее место в готовую последовательность. Рисунок 1 – Графическая схема алгоритма сортировки включениями Код программы, реализующей сортировку включениями: vector for (int i = 1; i < v.size(); i++) { int value = v[i]; int index = i; while ((index > 0) && (v[index - 1] > value)) { v[index] = v[index - 1]; index--; } v[index] = value; } return v; } Сортировка выбором – элементы массива условно разделяются на готовую последовательность 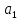, , …, 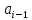и входную последовательность , , …, . 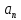На каждом шаге находится минимальный элемент  , который меняется местами с  -м элементом, который становится последним элементом готовой последовательности. Рисунок 2 – Графическая схема алгоритма сортировки выбором Код программы, реализующей сортировку включениями: vector for (int i = 0; i < v.size()-1; i++) { int min = i; for (int j = i + 1; j < v.size(); j++) { if (v[j] < v[min]) min = j; } swap(v[i], v[min]); } return v; } Сортировка обменами – сравниваются и обмениваются пары соседних элементов до тех пор, пока не будут отсортированы все элементы. Код программы, реализующей сортировку обменами: vector for (int i = 0; i < v.size()-1; i++) { bool f = 0; for (int j = 0; j < v.size()-i-1; j++) { if (v[j] > v[j + 1]) { swap(v[j], v[j + 1]); f = true; } } if (f == false) break; } return v; }  Рисунок 3 – Графическая схема алгоритма сортировки обменами Сортировка Шелла – модификация сортировки включениями. На первом шаге сравниваются элементы на расстоянии N/2, на каждом последующем шаге расстояние уменьшается в 2 раза, пока расстояние не станет равным единице. Код программы, реализующей сортировку Шелла: vector int step, i, j, tmp; for (step = v.size() / 2; step > 0; step /= 2) { for (i = step; i < v.size(); i++) { for (j = i - step; j >= 0 && v[j]>v[j + step]; j -= step) { tmp = v[j]; v[j] = v[j + step]; v[j + step] = tmp; } } } return v; } 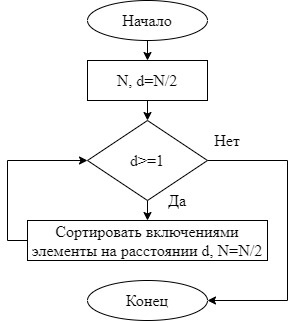 Рисунок 4 – Графическая схема алгоритма сортировки Шелла Сортировка Хоара – В массиве выбирается некоторый элемент, называемый разрешающим. Затем он помещается в то место массива, где ему полагается быть после упорядочивания всех элементов. В процессе отыскания подходящего места для разрешающего элемента производятся перестановки элементов так, что слева от них находятся элементы, меньшие разрешающего, и справа — большие (предполагается, что массив сортируется по возрастанию). Тем самым массив разбивается на две части: не отсортированные элементы слева от разрешающего элемента; не отсортированные элементы справа от разрешающего элемента. Чтобы отсортировать эти два меньших подмассива, алгоритм рекурсивно вызывает сам себя. Если требуется сортировать больше одного элемента, то нужно выбрать в массиве разрешающий элемент; переупорядочить массив, помещая элемент на его окончательное место; отсортировать рекурсивно элементы слева от разрешающего; отсортировать рекурсивно элементы справа от разрешающего. 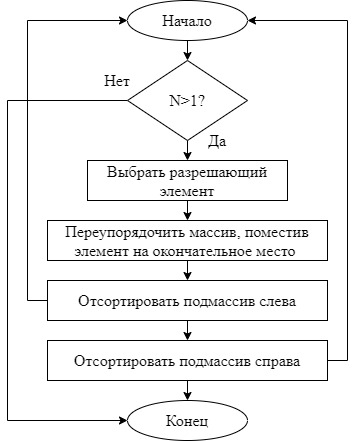 Рисунок 5 – Графическая схема алгоритма сортировки Хоара Код программы, реализующей сортировку Хоара: int hoar_partition(vector int pivot = v[(low + high) / 2]; int i = low - 1; int j = high + 1; while (true) { do { i = i + 1; } while (v[i] < pivot); do { j = j - 1; } while (v[j] > pivot); if (i >= j) return j; swap(v[i], v[j]); } } void hoar_sort(vector if (lo < hi) { int p = hoar_partition(v, lo, hi); hoar_sort(v, lo, p); hoar_sort(v, p + 1, hi); } } Пирамидальная сортировка – Общая идея пирамидальной сортировки заключается в том, что сначала строится пирамида из элементов исходного массива, а затем осуществляется сортировка элементов по построенной пирамиде.  Рисунок 6 – Графическая схема алгоритма пирамидальной сортировки Код программы, реализующей пирамидальную сортировку: vector for (int j = 0; j < v.size(); j++) { for (int i = v.size() / 2 - 1 - j / 2; i > -1; i--) { if (2 * i + 2 <= v.size() - 1 - j) { if (v[2 * i + 1] > v[2 * i + 2]) { if (v[i] < v[2 * i + 1]) { swap(v[i], v[2 * i + 1]); } } else if (v[i] < v[2 * i + 2]) { swap(v[i], v[2 * i + 2]); } } else if (2 * i + 1 <= v.size() - 1 - j) { if (v[i] < v[2 * i + 1]) { swap(v[i], v[2 * i + 1]); } } } swap(v[0], v[v.size() - 1 - j]); } return v; } Проверим эффективность сортировок на упорядоченном, неупорядоченном и обратно-упорядоченным массивах размерностями 5000, 10000, 15000 и 20000 элементов. В таблицах 1-3 указаны временные характеристики сортировок в секундах. Таблица 1 – Время работы сортировок на различном количестве элементов (исходный массив упорядоченный)
Таблица 2 – Время работы сортировок на различном количестве элементов (исходный массив неупорядоченный)
Таблица 3 – Время работы сортировок на различном количестве элементов (исходный массив обратно-упорядоченный)
На рисунках 7-12 изображены графики функций временной сложности алгоритмов сортировки. Зеленый – упорядоченный, желтый – неупорядоченный, красный – обратно-упорядоченный массивы соответственно.  Рисунок 7 – график функции временной сложности сортировки включениями  Рисунок 8 – график функции временной сложности сортировки выбором 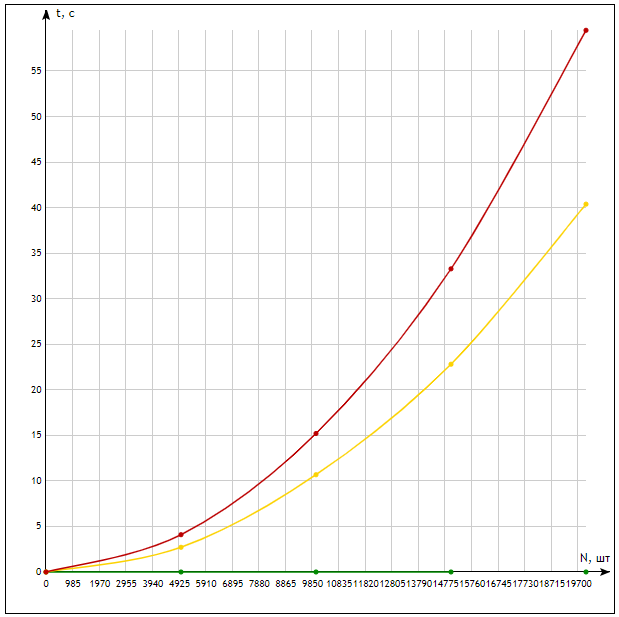 Рисунок 9 – график функции временной сложности сортировки обменами  Рисунок 10 – график функции временной сложности сортировки Шелла  Рисунок 11 – график функции временной сложности сортировки Хоара  Рисунок 12 – график функции временной сложности пирамидальной сортировки В результате экспериментов, можно сделать вывод, что сортировки обменом и включениями эффективнее прочих на упорядоченных массивах, наиболее универсальна и эффективна сортировка Хоара. Исследование алгоритмов поиска Для эксперимента будем использовать элемент, который содержится в массиве и элемент, который не содержится в массиве. Количество элементов 20000. Линейный поиск в неупорядоченном массиве заключается в последовательном сравнении искомого элемента с элементами массива поочередно. На каждом шаге проверяется не достигнут ли конец массива и не равен ли просматриваемый элемент искомому. 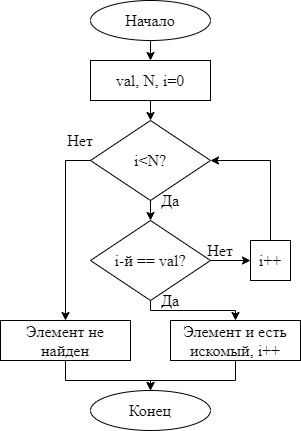 Рисунок 13 – Графическая схема алгоритма линейного поиска в неупорядоченном массиве Код программы, реализующей линейный поиск в неупорядоченном массиве: int linear_search(const vector int i = 0; while (i < v.size() && v[i] != val) i++; count_iter = i; return count_iter == v.size() ? -1 : i; } Быстрый линейный поиск в неупорядоченном массиве заключается в добавлении искомого элемента в конец массива и последовательном сравнении искомого элемента с элементами массива поочередно. На каждом шаге проверяется только не равен ли просматриваемый элемент искомому. Если элемент нашелся на N-й позиции, значит элемента в массиве нет. 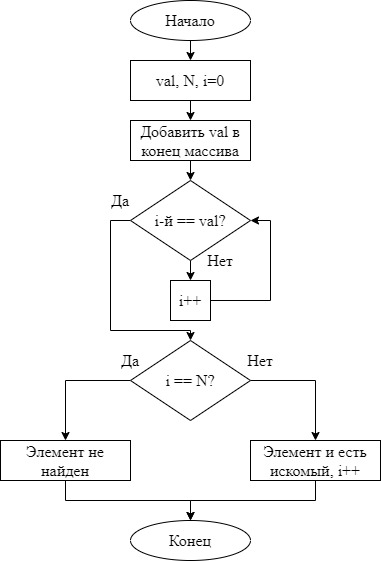 Рисунок 14 – Графическая схема алгоритма быстрого линейного поиска в неупорядоченном массиве Код программы, реализующей быстрый линейный поиск в неупорядоченном массиве: int linear_speed_search(vector int i = 0; v.push_back(val); while (v[i] != val) i++; v.pop_back(); count_iter = i; return count_iter == v.size() ? -1 : i; } Таблица 4 – Количество итераций, потраченных на нахождение элемента в неупорядоченном массиве
Вывод 1: количество итераций для линейного и быстрого линейного поиска одинаково, но на каждой итерации в быстром линейном поиске выполняется на одно сравнение меньше. Быстрый поиск в упорядоченном массиве заключается в последовательном сравнении искомого элемента с элементами массива поочередно. На каждом шаге проверяется не достигнут ли конец массива и является ли просматриваемый элемент меньшим чем искомый. Если просматриваемый элемент больше, чем искомый или если достигнут конец массива – элемент в массиве отсутствует.  Рисунок 15 – Графическая схема алгоритма быстрого поиска в упорядоченном массиве Код программы, реализующей быстрый поиск в упорядоченном массиве: int linear_speed_search_in_sorted(vector int i = 0; while (i count_iter = i; return i!=v.size()&&v[i]==val ? i : -1; } Бинарный поиск в упорядоченном массиве заключается в рекурсивном сравнении центрального элемента массива с искомым элементом. Если центральный элемент равен искомому – элемент найден, если центральный элемент больше искомого – рекурсивно произвести бинарный поиск в левой половине массива, если центральный элемент меньше искомого – рекурсивно произвести бинарный поиск в правой половине массива. 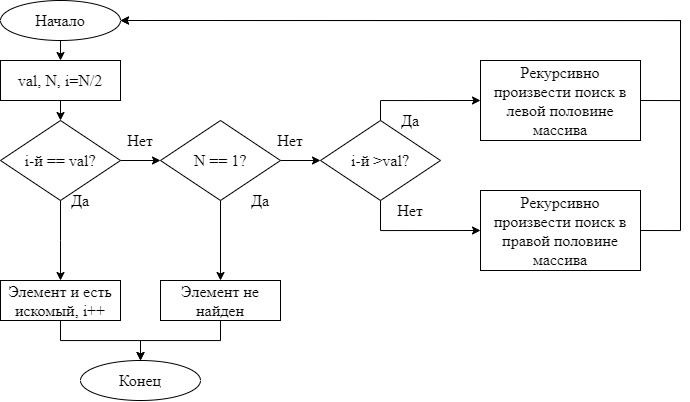 Рисунок 16 – Графическая схема алгоритма бинарного поиска в упорядоченном массиве Код программы, реализующей бинарный поиск в упорядоченном массиве: int binary_search(vector int i = 0, n = v.size()/2, index=n; while (n != 0) { i++; if (v[index] == val) { count_iter = i; return index; } else if (v[index] > val) index -= n/2; else index += n/2; n /= 2; } count_iter = i; return v[index] == val ? index : -1; } Блочный поиск в упорядоченном массиве заключается в разбиении исходного массива на блоки длинной  , сравнение происходит с первыми элементами каждого блока. При нахождении такого блока, первый элемент которого больше, чем искомый, последовательно проверяются все элементы предыдущего блока.  Рисунок 17 – Графическая схема алгоритма блочного поиска в упорядоченном массиве Код программы, реализующей блочный поиск в упорядоченном массиве: int block_search(vector int i_block = 0, n = sqrt(v.size()); while (i_block < v.size() && v[i_block] < val) i_block += n; count_iter = i_block / n; i_block -= n; int i = i_block; while (i < i_block + n && v[i] < val) i++; count_iter += (i - i_block); return v[i] == val ? i : -1; } Таблица 5 – Количество итераций, потраченных на нахождение элемента в упорядоченном массиве
Вывод 2: наиболее оптимальный алгоритм поиска в упорядоченном массиве – бинарный, позволяющий найти позицию элемента или доказать его несуществование в массиве за  итераций в худшем случае. |