тэф. Фатима Тэф. Тема изучение уравнения бернулли при движении жидкости в горизонтальной трубе переменного сечения
 Скачать 118.9 Kb.
|
|
3. ТЕМА ИЗУЧЕНИЕ УРАВНЕНИЯ БЕРНУЛЛИ ПРИ ДВИЖЕНИИ ЖИДКОСТИ В ГОРИЗОНТАЛЬНОЙ ТРУБЕ ПЕРЕМЕННОГО СЕЧЕНИЯ. ВОПРОСЫ: 1. Основные понятия гидродинамики. 2. Уравнение неразрывности потока. 3. Уравнение Бернулли для элементарной струйки идеальной жидко-сти. 4. Уравнение Бернулли для потока реальной жидкости. Потери напора жидкости. 5. Диаграмма Бернулли; пьезометрическая и напорная линии. 6. Устройство и принцип работы карбюратора, струйного насоса, труб-ного расходомера Вентуры, трубки Прандтля. ОТВЕТЫ : 1.Основные понятия. Уравнение Бернулли является основным уравнением гидродинамики - раз-дела гидравлики, изучающего законы движения жидкостей и их взаимодействия со стенками. Наиболее важными понятиями гидродинамики являются: идеальная жидкость, стационарное течение, линия и трубка тока, напор, напорное течение, живое сечение, смоченный периметр, объемный расход. 2. Уравнение неразрывности струи. Через любое живое сечение трубки тока за данный промежуток времени проходит одинаковый объем жидкости, т.е. объемный расход через любое сечение трубки тока есть величина постоянная: Q = υ · s = const или υ1 · s1 = υ2 · s2 , где s1 , s2 - площади сечения; υ1 , υ2 -скорости жидкости в этих сечениях. 3. Уравнение Бернулли для элементарной струйки идеальной жидко-сти. Течение идеальной жидкости совершается без потерь энергии жидкости (нет сил трения). Следовательно, в любом сечении элементарной струйки идеальной жидкости полный гидродинамический напор, равный сумме гео-метрического ,пьезометрического напоров есть величиной постоянная. Уравнение Бернулли для элементарной струйки идеальной жидкости имеет вид H=z+Pρg+υ22g=const или H1=H2 или z1+P1ρg+υ122g= z1+P2ρg+υ222g. 4. Уравнение Бернулли для потока реальной жидкости. Потери напора жидкости. В реальной жидкости часть энергии жидкости расходуется на работу про-тив сил внутреннего трения. В результате полная энергия, следовательно, и гидродинамический напор жидкости вдоль потока непрерывно уменьшается, т.е. Н1 > Н2. Потери напора между сечениями 1 и 2 h = Н1 - Н2 . Из этого получим уравнение Бернулли для реальной жидкости: H1=H2+ h или z1+ 𝑃1ρg+α·υ222g+h . 5. Диаграмма Бернулли; пьезометрическая и напорная линии. Диаграмма уравнения Бернулли является графическим представлением изменения различных слагаемых уравнения Бернулли по длине трубопровода. Диаграмма характеризует удельную механическую энергию потока и включает в себя три линии: линию полного напора, пьезометрическую линию и линию геометрического напора. Линия полного напора характеризует полную удельную механическую энергию, то есть сумму кинетической и потенциальной энергий:  ,при этом удельная потенциальная энергия давления  при построении диаграммы определяется не абсолютным давлением, а избыточным.Пьезометрическая линия характеризует удельную потенциальную энергию потока и представляет сумму двух слагаемых  .Геометрическая линия, или линия геометрического напора характеризует уклон трубопровода, т. е. изменение координаты z оси трубопровода. 6. Карбюратор. Карбюратор предназначен для образования рабочей смеси топлива в поршневых двигателях внутреннего сгорания, т. е. для подсоса бензина и смешивания его с воздухом. Струйный насос. Струйный насос нашел широкое применение в технике. Иногда его называют эжектором.. Струйные насосы применяются в жидкостных реактивных двигателях. Трубчатый расходомер Вентури. Этот измерительный прибор имеет ряд достоинств. Он прост в изготовлении и эксплуатации (в нем отсутствуют какие-либо движущиеся части), имеет низкую стоимость, характеризуется незначительными потерями напора. Прибор можно использовать для измерения расхода как однородных, так и неоднородных жидкостей, широко применяется в лабораторных и промышленных условиях. Гидродинамические трубки. Гидродинамические трубки предназначены для измерения местных скоростей в отдельных точках живого сечения потока жидкости. Усовершенствованная трубка Прандтля позволяет измерять скоростной и пьезометрический напоры 4. ТЕМА ОПРЕДЕЛЕНИЕ ПОТЕРЬ НАПОРА ЖИДКОСТИ ПО ДЛИНЕ ТРУБОПРОВОДА. ВОПРОСЫ: 1. Определение понятий: напор жидкости, напорное течение, живое сече-ние потока, объемный расход, шероховатости: абсолют-ная, эквивалентная и относительная. 2. Сила внутреннего трения. Динамическая и кинематическая вязкости во-ды 3. Потери напора по длине трубопровода. Формула Дарси- Фейсбаха. 4. Характеристика областей течения. Формулы для определения коэффи-циента гидравлического трения. 5. Уравнение Бернулли для потока реальной жидкости. ОТВЕТЫ : Напор — (в гидравлике и гидромеханике) величина давления жидкости (или газа), выражаемая высотой столба жидкости (газа) над выбранным уровнем отсчёта; измеряется в линейных единицах (метрах). Напорным называется движение жидкости, при котором поток полностью заключен в твердые стенки и не имеет свободной поверхности. Напорное движение происходит вследствие разности д Живое сечение ω - это поперечное сечение потока, нормальное ко всем линиям тока его пересекающим . Смоченный периметр c - линия, по которой жидкость соприкасается с поверхностями русла. Объёмный расход — в гидравлике объём жидкости или газа, протекающей через поперечное сечение потока в единицу времени. или. где: Q — объёмный расход жидкости или газа, м³/с; V — объём жидкости или газа, проходящий через поперечное сечение потока за время t, м³; t — время... Абсолютной шероховатостью k называют среднюю высоту выступов шероховатости. Опыты показали, что при одной и той же величине абсолютной шероховатости влияние ее на величину гидравлического сопротивления различно в зависимости от диаметра трубы. Поэтому вводится величина относительной шероховатости. Относительной шероховатостью называется отношение абсолютной шероховатости к диаметру трубы, т.е.  эквивалентной шероховатостью Эта шероховатость пред ставляет собой выступы равномерно распределенной зернис той абсолютной шероховатости такого размера, который дает при подсчетах одинаковые с действительной шероховатостью потери напора 2. Вязкость (внутреннее трение) (англ. viscosity) — одно из явлений переноса, свойство текучих тел (жидкостей и газов) оказывать сопротивление перемещению одной их части относительно другой. Механизм внутреннего трения в жидкостях и газах заключается в том, что хаотически движущиеся молекулы переносят импульс из одного слоя в другой, что приводит к выравниванию скоростей — это описывается введением силы трения. Вязкость твёрдых тел обладает рядом специфических особенностей и рассматривается обычно отдельно. Основной закон вязкого течения был установлен И. Ньютоном (1687): В применении к жидкостям различают вязкость: Динамическая (абсолютная) вязкость µ – сила, действующая на единичную площадь плоской поверхности, которая перемещается с единичной скоростью относительно другой плоской поверхности, находящейся от первой на единичном расстоянии. В системе СИ динамическая вязкость выражается в Па×с (паскаль-секунда), внесистемная единица П (пуаз). Кинематическая вязкость ν – отношение динамической вязкости µ к плотности жидкости ρ. ν= µ/ρ, где: ν, м2/с – кинематическая вязкость; μ, Па×с – динамическая вязкость; ρ, кг/м3 – плотность жидкости. 3. Потери напора по длине трубопровода вычисляются по формуле Дарси — Вейсбаха.  Потери напора и давления связаны зависимостью. Δp=Δhρg где ρ - плотность, g - ускорение свободного падения. Потери давления по длине можно вычислить используя формулу Дарси — Вейсбаха.  4.--- 5. Если на участке между расчетными сечениями не совершается механическая работа, а движение является установившимся, без притока и отбора жидкости, и сама жидкость является несжимаемой, то для потока будут справедливы зависимости: Н1=Н2 + Δh1 - 2 z1 + p1/ρg + V12/2g = z2 + p2/ρg + V22/2g + Δh1 - 2 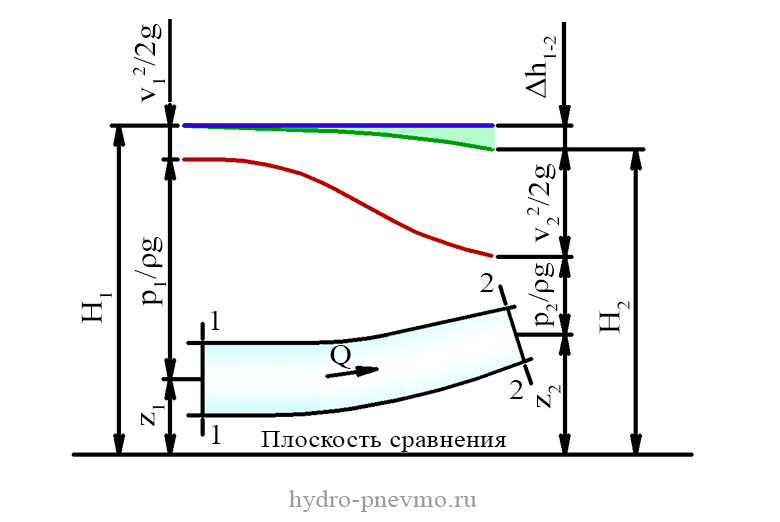 Уравнение Бернулли устанавливает связь между полными напорами потока жидкости на участке ограниченными сечениями 1-1 и 2-2. В соответствии с уравнением Бернулли полный напор потока Hi уменьшается от сечения 1-1 к сечению 2-2 на величину потерь напора (энергии) h1 - 2, вызванных гидравлическими сопротивлениями участка. 5. ТЕМА ИЗУЧЕНИЕ ПОТЕРЬ НАПОРА ЖИДКОСТИ НА МЕСТНЫХ СОПРОТИВЛЕНИЯХ. ВОПРОСЫ: 1. Определения понятий: напор жидкости, скоростной напор, пьезо-метрический напор, геометрический напор, напорное течение, местное со-противление, коэффициент сжатия струи, коэффициент местного сопро-тивления, эквивалентная длина местного сопротивления, объемный расход жидкости; 2. Характеристика основных типов местных сопротивлений; 3. Формула Дарси, ее содержание; 4. Зависимость коэффициентов местных сопротивлений от числа Рейнольдса; 5. Явный вид уравнения Бернулли для потока реактивной жидкости. Ответы : 1. Местными сопротивлениями называются такие локализованные элемен-ты трубопровода, на прохождение которых теряется часть энергии потока жид-кости. Потери напора на местных сопротивлениях прямо пропорциональны ско-ростному напору жидкости и определяются по формуле Дарси: ℎ=𝜉𝜐22𝑔 Сжатие струи оценивается коэффициентом сжатия ε, равным отношению площади поперечного сечения струи к площади отверстия ε = Sc/S0= (dc/d0)2. Коэффициент местного сопротивления зависит от формы и вида местного сопротивления, шероховатости воздуховода и как ни странно от числа Рейнольдса. Для заслонок и другой запорной арматуры к перечисленному додается еще степень открытия. Связанность КМС с числом Рейнольдса выражается в формуле  Эквивалентная длина – такая длина прямого участка трубопровода данного диаметра, на которой потери на трение по длине эквивалентны потери напора, вызываемой данным местным сопротивлением, т.е.  . Таким образом, для определения потери напора на местном сопротивлении, мы мысленно заменяем местное сопротивление прямой трубой эквивалентной длины. Это позволяет нам применить формулу Дарси-Вейсбаха для определения потерь напора на местном сопротивлении и учесть изменение числа Re.
Объёмный расход — в гидравлике объём жидкости или газа, протекающей через поперечное сечение потока в единицу времени. {\displaystyle Q={\frac {V}{t}}} {\displaystyle Q=\upsilon *S,} 2. Местные сопротивления подразделяются на простые и сложные. К простым сопротивлениям относятся: внезапное сужение и расширение потока, поворот русла. К сложным – сопротивления, представляющие собой комбинацию простых местных сопротивлений (задвижка, клапан и т. д.). В зависимости от факторов вызывающих потери напора, в местных сопротивлениях различают потери трения и вихревые потери. Потери на трение вызываются торможением потока стенами. Вихревые потери связаны с отрывами потока от стенок, происходящими при изменении конфигурации русла. 3. Формула Дарси Вейсбаха'[1] в гидравлике — эмпирическая формула, определяющая потери напора или потери давления при развитом турбулентном течении несжимаемой жидкости на гидравлических сопротивлениях (предложена Юлиусом Вейсбахом в 1855 году): {\displaystyle \Delta h=\xi \cdot {\frac {V^{2}}{2g}},} 4.Коэффициент местного сопротивления зависит от формы и вида местного сопротивления, шероховатости воздуховода и как ни странно от числа Рейнольдса. Для заслонок и другой запорной арматуры к перечисленному додается еще степень открытия. Связанность КМС с числом Рейнольдса выражается в формуле Суммарный коэффициент местных сопротивлений на участке воздуховода равен сумме всех местных коэффициентов на этом участке. |
