Транспортная задача. Тема Линейное программирование. Транспортная задача. Метод потенциалов. Задание
 Скачать 74.55 Kb. Скачать 74.55 Kb.
|
|
Тема: Линейное программирование. Транспортная задача. Метод потенциалов. Задание: составить оптимальный план распределения поставок. Начальный базисный план перевозок можно сделать любым известным способом. Стоимость перевозки единицы груза, а также потребности и наличие груза даны в таблице.
Решение Методом минимального элемента составляем начальный план перевозок. Так как 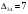 (минимальный элемент), то в него помещаем 80, оставшиеся ячейки в четвертом столбце будут пустыми так как весь груз на данном объекте распределен. В ячейку (минимальный элемент), то в него помещаем 80, оставшиеся ячейки в четвертом столбце будут пустыми так как весь груз на данном объекте распределен. В ячейку 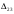 помещаем 85, а в ячейку помещаем 85, а в ячейку 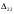 помещаем 5, так как другие ячейки строки 2 не могут быть заполнены. помещаем 5, так как другие ячейки строки 2 не могут быть заполнены.В ячейку 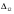 помещаем 115, так как в этой ячейке находится минимальная стоимость из всех оставшихся. На данном объекте осталось 30 единиц груза, его помещаем в ячейку помещаем 115, так как в этой ячейке находится минимальная стоимость из всех оставшихся. На данном объекте осталось 30 единиц груза, его помещаем в ячейку 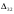 , так как это последний оставшийся потребитель, который готов приобрести последний оставшийся груз. , так как это последний оставшийся потребитель, который готов приобрести последний оставшийся груз.
Для каждой заполненной клетки записываем уравнение потенциалов: 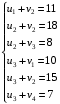 , где ui – номер строки, а vj- номер столбца , где ui – номер строки, а vj- номер столбцаРешая систему уравнений получаем: 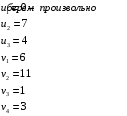 Составим разности потенциалов для свободных клеток: 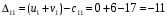 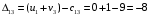 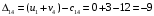 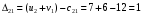 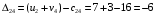 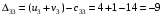 Так как 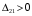 , то опорное решение не является оптимальным и его можно улучшить, перейдя от одного опорного решения к другому. , то опорное решение не является оптимальным и его можно улучшить, перейдя от одного опорного решения к другому.  Для свободной клетки (2;1), имеющей положительную оценку ( Для свободной клетки (2;1), имеющей положительную оценку (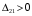 ) строится цикл. ) строится цикл.У вершин со знаком (-) выбираем минимальный груз, он равен 5. Его прибавляем к грузам, стоящих у положительных вершин, и отнимаем от грузов, стоящих у отрицательных вершин. После перераспределения груза в пределах цикла имеем следующую транспортную таблицу. Транспортная таблица не является окончательной, поэтому выполняем дальнейшие расчёты.
Для каждой заполненной клетки записываем уравнение потенциалов: 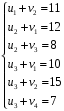 , где ui – номер строки, а vj- номер столбца , где ui – номер строки, а vj- номер столбцаРешая систему уравнений получаем: 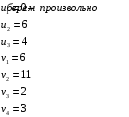 Составляем разности потенциалов для свободных клеток: 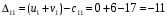 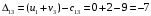 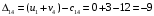 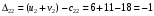 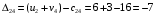 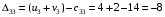 Получили, что все оценки свободных клеток отрицательные, следовательно, найденное решение оптимальное. Найденный план оптимальный. 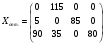 Стоимость перевозок равна: 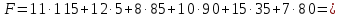 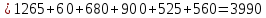 Ответ: 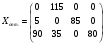 Стоимость перевозок равна: F= 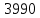 . . |
