задачи по микроэкономике. КРУГЛОВ И.В.ЗАДАЧИ ПО МИКРОЭКОНОМИКЕ ТЕМЫ 5-6 ЛГТУ. Тема Основы теории производства
 Скачать 0.98 Mb.
|
|
Задача 6.20. Производственная функция фирмы имеет вид  ( - количество капитала,  - количество труда). Цены на выпускаемую продукцию и ресурсы равны  . Найдите:а) локальное рыночное равновесие фирмы (  );б) доход  , издержки  и максимальную прибыль  .Задача 6.21. Технологическое множество 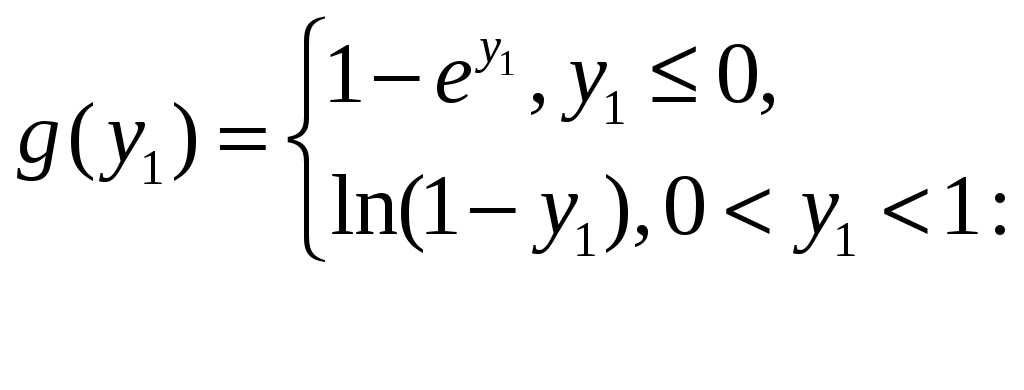 фирмы  имеет вид   , где  а) постройте это множество на плоскости  ;б) найдите сумму  , опишите аналитически северо-восточную (эффективную) границу множества . Постройте множество .Ответ обоснуйте.Задача 6.22. В моделируемой системе два продукта (продукт и ресурс), одна фирма и два потребителя  и  Технологическое множество фирмы описано в задаче 6.21.Доли потребителей в прибыли фирмы равны  У потребителя  начальный запас  и функция полезности  У потребителя  начальный запас  и функция полезности  а) найдите локальное рыночное равновесие фирмы ;б) найдите локальное равновесие у каждого потребителя и ;в) выпишите вектор избыточного спроса; г) найдите цены равновесия (нормированные). Выпишите статистическое экономическое равновесие; д)постройте множество на плоскости  Задача 6.23. В экономической системе два продукта (продукт и ресурс), две фирмы 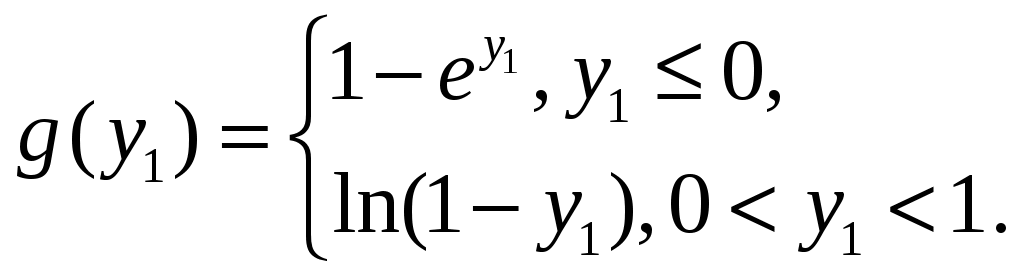 и два потребителя  . Технологическое множество  фирмы  имеет вид  Технологическое множество  фирмы  имеет вид , где  Доля потребителей в прибыли фирмы и фирмы соответственно равны  У потребителя начальный запас  и функция полезности  У потребителя начальный запас  и функция полезности  а) найдите локальное рыночное равновесие каждой фирмы; б) найдите локальное равновесие дляу каждого потребителя; в) выпишите вектор избыточного спроса; г) найдите цены равновесия (нормированные). Выпишите статистическое экономическое равновесие; д)постройте множество  и  Задача 6.24. Количество выпускаемой продукции V и потребление фактора производства Х составило V, шт. 220 236 248 256 260 Х, шт. 110 120 130 140 150. Какое количество фактора Х будет применять фирма, что бы добиться максимума прибыли, если цена фактора Рх = 2,5 руб./шт., считая, что потребление других факторов неизменно? Цена продукции Рv=1руб/шт. Задача 6.25. Дано: производство достигло оптимума по соотношению и количеству применяемых факторов производства и выработке продукции. Затраты на каждый из двух факторов производства х1 и х2 - 100 тыс. руб. Выручка общая - 300 тыс. руб. Используется фактора х1 - 100 ед. ф. , выработка продукции - 3000 ед. прод. Определить: отдачу от масштаба, на сколько уменьшится объем выручки, если уменьшить объем потребления фактора х1 на 10 ед. ф. Задача 6.26. Обнаружено, что при остановке автоматического станка происходит уменьшение выработки за день с 200 ед. прод. до 180 ед.прод. В случае невыхода на работу 10 сотрудников уменьшение объема производства составляет с 200 ед. прод. до 190 ед. прод. Сколько сотрудников можно сократить безболезненно для объема выпуска, если купить дополнительно 1 станок? Как этот показатель называется на языке экономической теории? Задача 6.27. На оптимальное соотношение факторов производства. Цена рабочей силы - 1000 руб. Цена работы единицы оборудования - 2000 руб. Какой прирост производства продукции принесет найм трех дополнительных рабочих, если только что установленный станок привел к увеличению объема производства на 100 ед. прод., считая, что структура производства оптимальна. Задача 6.28. Построить производственную функцию методом изоквант, найти линию оптимального производства (графически) при ценах факторов производства Рх1 = 2 руб./шт., Рх2 = 4 руб,/шт. Производственная функция 1/2 1/2 F ( х1,х2) = х1 * х2. Задача 6.29. Дана функция общих экономических издержек одной фирмы. ТС (q) = 0.02 q*(q – 20) 2 + 5*q + 125 а) найти объем постоянных издержек FC - найти и построить функции общих средних издержек АТС, средних переменных издержек AVC, предельных издержек МС - Найти оптимальный объем производства и прибыль фирмы, если рыночная цена продукции Р = 20 б) В совершенно конкурентной отрасли действуют несколько таких же фирм. Функция спроса отрасли Q(p) = 1500 - 50 р Найти объем производства в отрасли, цену продукции, количество работающих фирм в долгосрочном периоде. Задача 6.30. Дана функция переменных издержек VC (Q) фирмы. Фирма способна при постоянной цене продукции Р = 36 окупить все свои издержки, поддерживая объем производства не менее Qбез. = 20. Найти функцию прибыли (убытков), функцию предложения фирмы, точку максимальной прибыли и точку минимума средних издержек. Проиллюстрировать графиком. Q 10 20 30 40 50 VC 100 220 390 640 1100. Задача 6.31. 1)Пространство продуктов (ресурсов)  2)Технологическое множество фирмы имеет вид Технологическое множество фир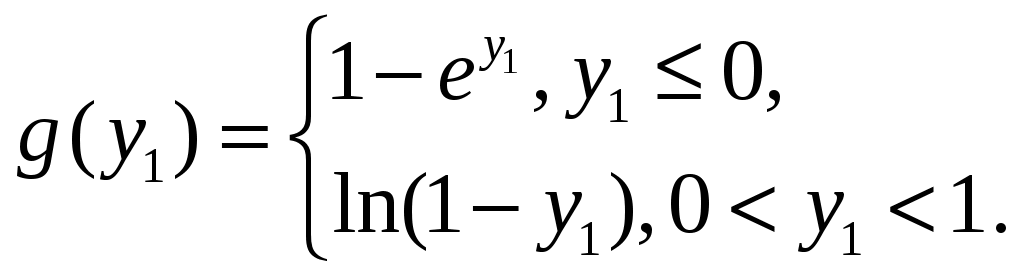мы имеет вид , где 3) Потребитель имеет начальный запас  и функцию полезности  , потребитель имеет начальный запас  и функцию полезности  ;4) доли потребителей и в прибыли фирмы равны  и  ; в прибыли фирмы соответственно равны  Требуется построить технологические множества и , найти для вектора цен  локальное рыночное равновесие, максимальную прибыль каждой фирмы и , найти локальное рыночное равновесие для каждого потребителя и , выписать избыточный спрос, найти нормированные цены равновесия, статическое экономическое равновесие, построить множества  Задача 6.32. 1)Пространство продуктов (ресурсов) 2) Два потребителя и с характеристиками:Потребитель имеет начальный запас  и функцию полезности , потребитель имеет начальный запас  и функцию полезности ;3) фирма имеет технологическое множество  4) доли потребителей и в прибыли фирмы равны  Требуется построить технологическое множество и найти для вектора цен локальное рыночное равновесие, максимальную прибыль фирмы , найти локальное рыночное равновесие для каждого потребителя и , выписать избыточный спрос, найти нормированные цены равновесия, статическое экономическое равновесие. Задача 6.33. Фирма-монополист имеет два сегмента рынка, на каждом из которых функция, обратная функции спроса, имеет вид  и  . Предельные издержки фирмы постоянны и равны  :а) определите выпуск  , цену  и максимальную прибыль  в фирмы в первом сегменте;б) определите выпуск  , цену  и максимальную прибыль  в фирмы во втором сегменте;в) определите суммарный выпуск  и суммарную прибыль  . |