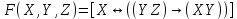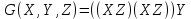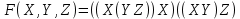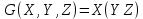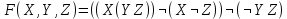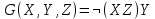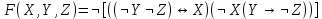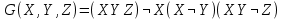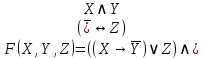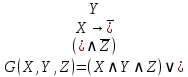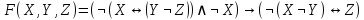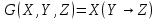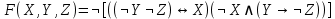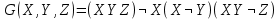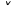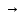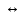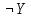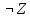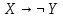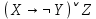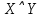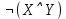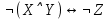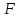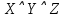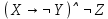Задание 1(24). Тема Основные понятия алгебры высказываний
 Скачать 77.66 Kb. Скачать 77.66 Kb.
|
Практическое задание 1Тема 1.1. Основные понятия алгебры высказываний Задание 1 Составив таблицы истинности, выясните, равносильны ли формулы алгебры высказываний из таблицы 1.1. Таблица 1.1
Рекомендации по выполнению задания Номер варианта задания определить по первой букве фамилии студента, используя таблицу 1.2. Решение расписывать как можно подробнее, обязательно описывать формулы, используемые при решении. Обязательно должны быть записаны условие задания, ответ. Таблица 1.2 Выбор варианта задания
Образец выполнения задания Задание Составив таблицы истинности, выясните, равносильны ли следующие формулы алгебры высказываний: 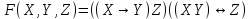 , ,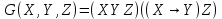 . .Решение Будем использовать таблицы истинности конъюнкции, дизъюнкции, импликации и эквивалентности.
Таблица истинности формулы F
Таблица истинности формулы G
Формулы F и G не эквивалентны, так как их значения различаются на наборе (1, 1, 1). Введённая функция: X∧(Y→Z)∨¬X∨¬Z≡¬¬Y≡Z Вектор функция: 00111011 Таблица истинности:
Совершенная дизъюнктивная нормальная форма (СДНФ)¬XY¬Z ∨ ¬XYZ ∨ X¬Y¬Z ∨ XY¬Z ∨ XYZ Совершенная конъюнктивная нормальная форма (СKНФ)(X∨Y∨Z) ∧ (X∨Y∨¬Z) ∧ (¬X∨Y∨¬Z) Полином ЖегалкинаY⊕X⊕XZ⊕XY⊕XYZ РешениеПостроение совершенной дизъюнктивной нормальной формы:Найдём наборы, на которых функция принимает истинное значение: { 0, 1, 0 } { 0, 1, 1 } { 1, 0, 0 } { 1, 1, 0 } { 1, 1, 1 } В соответствие найденным наборам поставим элементарные конъюнкции по всем переменным, причём если переменная в наборе принимает значение 0, то она будет записана с отрицанием: K1: { 0, 1, 0 } — ¬XY¬Z K2: { 0, 1, 1 } — ¬XYZ K3: { 1, 0, 0 } — X¬Y¬Z K4: { 1, 1, 0 } — XY¬Z K5: { 1, 1, 1 } — XYZ Объединим конъюнкции с помощью операции ИЛИ и получим совершенную дизъюнктивную нормальную форму: K1 ∨ K2 ∨ K3 ∨ K4 ∨ K5 = ¬XY¬Z ∨ ¬XYZ ∨ X¬Y¬Z ∨ XY¬Z ∨ XYZ Построение совершенной конъюнктивной нормальной формы:Найдём наборы, на которых функция принимает ложное значение: { 0, 0, 0 } { 0, 0, 1 } { 1, 0, 1 } В соответствие найденным наборам поставим элементарные дизъюнкции по всем переменным, причём если переменная в наборе принимает значение 1, то она будет записана с отрицанием: D1: { 0, 0, 0 } — X∨Y∨Z D2: { 0, 0, 1 } — X∨Y∨¬Z D3: { 1, 0, 1 } — ¬X∨Y∨¬Z Объединим дизъюнкции с помощью операции И и получим совершенную конъюнктивную нормальную форму: D1 ∧ D2 ∧ D3 = (X∨Y∨Z) ∧ (X∨Y∨¬Z) ∧ (¬X∨Y∨¬Z) Построение полинома Жегалкина методом Паскаля:
Построение полинома Жегалкина методом треугольника:
1. Строится треугольная таблица, в которой первый столбец совпадает со столбцом значений функции в таблице истинности. 2. Ячейка в каждом последующем столбце получается путём сложения по модулю 2 двух ячеек предыдущего столбца — стоящей в той же строке и строкой ниже. 3. Столбцы вспомогательной таблицы нумеруются двоичными кодами в том же порядке, что и строки таблицы истинности. 4. Каждому двоичному коду ставится в соответствие один из членов полинома Жегалкина в зависимости от позиций кода, в которых стоят единицы. 5. Если в верхней строке какого-либо столбца стоит единица, то соответствующий член присутствует в полиноме Жегалкина. Построение полинома Жегалкина методом неопределённых коэффициентов:Запишем данную функцию в виде полинома Жегалкина с неопределёнными коэффициентами: f(X,Y,Z) = a000 ⊕ a001Z ⊕ a010Y ⊕ a100X ⊕ a011YZ ⊕ a101XZ ⊕ a110XY ⊕ a111XYZ f(0,0,0) = a000 = 0 ⇒ a000 = 0 f(0,0,1) = a000 ⊕ a001 = 0 ⊕ a001 = 0 ⇒ a001 = 0 f(0,1,0) = a000 ⊕ a010 = 0 ⊕ a010 = 1 ⇒ a010 = 1 f(1,0,0) = a000 ⊕ a100 = 0 ⊕ a100 = 1 ⇒ a100 = 1 f(0,1,1) = a000 ⊕ a001 ⊕ a010 ⊕ a011 = 0 ⊕ 0 ⊕ 1 ⊕ a011 = 1 ⇒ a011 = 0 f(1,0,1) = a000 ⊕ a001 ⊕ a100 ⊕ a101 = 0 ⊕ 0 ⊕ 1 ⊕ a101 = 0 ⇒ a101 = 1 f(1,1,0) = a000 ⊕ a010 ⊕ a100 ⊕ a110 = 0 ⊕ 1 ⊕ 1 ⊕ a110 = 1 ⇒ a110 = 1 f(1,1,1) = a000 ⊕ a001 ⊕ a010 ⊕ a100 ⊕ a011 ⊕ a101 ⊕ a110 ⊕ a111 = 0 ⊕ 0 ⊕ 1 ⊕ 1 ⊕ 0 ⊕ 1 ⊕ 1 ⊕ a111 = 1 ⇒ a111 = 1 Окончательно получаем: Y ⊕ X ⊕ XZ ⊕ XY ⊕ XYZ Введённая функция: X→Z∨Y Вектор функция: 11110111 Таблица истинности:
Совершенная дизъюнктивная нормальная форма (СДНФ)¬X¬Y¬Z ∨ ¬X¬YZ ∨ ¬XY¬Z ∨ ¬XYZ ∨ X¬YZ ∨ XY¬Z ∨ XYZ Совершенная конъюнктивная нормальная форма (СKНФ)¬X∨Y∨Z Полином Жегалкина1⊕X⊕XZ⊕XY⊕XYZ РешениеПостроение совершенной дизъюнктивной нормальной формы:Найдём наборы, на которых функция принимает истинное значение: { 0, 0, 0 } { 0, 0, 1 } { 0, 1, 0 } { 0, 1, 1 } { 1, 0, 1 } { 1, 1, 0 } { 1, 1, 1 } В соответствие найденным наборам поставим элементарные конъюнкции по всем переменным, причём если переменная в наборе принимает значение 0, то она будет записана с отрицанием: K1: { 0, 0, 0 } — ¬X¬Y¬Z K2: { 0, 0, 1 } — ¬X¬YZ K3: { 0, 1, 0 } — ¬XY¬Z K4: { 0, 1, 1 } — ¬XYZ K5: { 1, 0, 1 } — X¬YZ K6: { 1, 1, 0 } — XY¬Z K7: { 1, 1, 1 } — XYZ Объединим конъюнкции с помощью операции ИЛИ и получим совершенную дизъюнктивную нормальную форму: K1 ∨ K2 ∨ K3 ∨ K4 ∨ K5 ∨ K6 ∨ K7 = ¬X¬Y¬Z ∨ ¬X¬YZ ∨ ¬XY¬Z ∨ ¬XYZ ∨ X¬YZ ∨ XY¬Z ∨ XYZ Построение совершенной конъюнктивной нормальной формы:Найдём наборы, на которых функция принимает ложное значение: { 1, 0, 0 } В соответствие найденным наборам поставим элементарные дизъюнкции по всем переменным, причём если переменная в наборе принимает значение 1, то она будет записана с отрицанием: D1: { 1, 0, 0 } — ¬X∨Y∨Z Объединим дизъюнкции с помощью операции И и получим совершенную конъюнктивную нормальную форму: D1 = (¬X∨Y∨Z) Построение полинома Жегалкина методом Паскаля:
Построение полинома Жегалкина методом треугольника:
1. Строится треугольная таблица, в которой первый столбец совпадает со столбцом значений функции в таблице истинности. 2. Ячейка в каждом последующем столбце получается путём сложения по модулю 2 двух ячеек предыдущего столбца — стоящей в той же строке и строкой ниже. 3. Столбцы вспомогательной таблицы нумеруются двоичными кодами в том же порядке, что и строки таблицы истинности. 4. Каждому двоичному коду ставится в соответствие один из членов полинома Жегалкина в зависимости от позиций кода, в которых стоят единицы. 5. Если в верхней строке какого-либо столбца стоит единица, то соответствующий член присутствует в полиноме Жегалкина. Построение полинома Жегалкина методом неопределённых коэффициентов:Запишем данную функцию в виде полинома Жегалкина с неопределёнными коэффициентами: f(X,Y,Z) = a000 ⊕ a001Z ⊕ a010Y ⊕ a100X ⊕ a011YZ ⊕ a101XZ ⊕ a110XY ⊕ a111XYZ f(0,0,0) = a000 = 1 ⇒ a000 = 1 f(0,0,1) = a000 ⊕ a001 = 1 ⊕ a001 = 1 ⇒ a001 = 0 f(0,1,0) = a000 ⊕ a010 = 1 ⊕ a010 = 1 ⇒ a010 = 0 f(1,0,0) = a000 ⊕ a100 = 1 ⊕ a100 = 0 ⇒ a100 = 1 f(0,1,1) = a000 ⊕ a001 ⊕ a010 ⊕ a011 = 1 ⊕ 0 ⊕ 0 ⊕ a011 = 1 ⇒ a011 = 0 f(1,0,1) = a000 ⊕ a001 ⊕ a100 ⊕ a101 = 1 ⊕ 0 ⊕ 1 ⊕ a101 = 1 ⇒ a101 = 1 f(1,1,0) = a000 ⊕ a010 ⊕ a100 ⊕ a110 = 1 ⊕ 0 ⊕ 1 ⊕ a110 = 1 ⇒ a110 = 1 f(1,1,1) = a000 ⊕ a001 ⊕ a010 ⊕ a100 ⊕ a011 ⊕ a101 ⊕ a110 ⊕ a111 = 1 ⊕ 0 ⊕ 0 ⊕ 1 ⊕ 0 ⊕ 1 ⊕ 1 ⊕ a111 = 1 ⇒ a111 = 1 Окончательно получаем: 1 ⊕ X ⊕ XZ ⊕ XY ⊕ XYZ |