Задание 2(5). Тема Передаточные механизмы
 Скачать 2.17 Mb. Скачать 2.17 Mb.
|
2.2. Проектирование передачи1. Ориентировочно значение модуля при проектировочном расчете зубчатых передач можно принять, мм: – при твердости Н350НВ m= (0,01...0,02)aw; (2.11) – при твердости H45HRCэ т = (0,016...0,0315)aw. (2.12) По ГОСТ 9563–80 принимают стандартный нормальный модуль: РЯД 1 – 1; 1,25; 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10; 12; 16; РЯД 2 – 1,125; 1,375; 1,75; 2,25; 2,75; 3,5; 4,5; 5,5; 7; 9; 11; 14. Значения первого ряда следует предпочитать значениям второго. 2. Определяется суммарное число зубьев и число зубьев шестерни и колеса: – предварительно принимают угол наклона зубьев 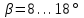 и определяют суммарное zC число зубьев шестерни z1 и колеса z2: и определяют суммарное zC число зубьев шестерни z1 и колеса z2: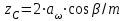 ; (2.13) ; (2.13)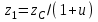 ; (2.14) ; (2.14)– полученные значения чисел зубьев округляем до целого числа: z2 = zС –z1. (2.15) 3. Определяются действительное передаточное число и его погрешность: 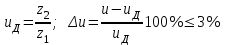 . (2.16) . (2.16)Погрешность передаточного числа не должна превышать 3 %. 4. Уточняем значение угла 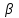 : :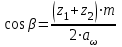 , (2.17) , (2.17)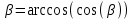 . (2.18) . (2.18)Значение угла наклона зубьев необходимо вычислять с точностью до секунд. 5. Далее определяются основные размеры шестерни и колеса. Делительные диаметры шестерни и колеса: 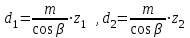 . (2.19) . (2.19)6. Проверку полученных диаметров можно провести с помощью формулы 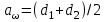 . (2.20) . (2.20)Проверкой должно быть установлено, что межосевое расстояние сходится со значением, принятым ранее. 7. Диаметры вершин зубьев определяются по формуле: 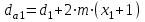 , , 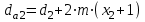 ; (2.21) ; (2.21)диаметры впадин: 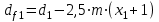 , , 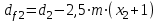 , (2.22) , (2.22)где x – коэффициент смещения, мм. 8. Ширина колеса определяется по формуле, мм: 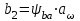 . (2.23) . (2.23)Полученное значение ширины колеса округляем до нормального линейного размера. 9. Ширина шестерни определяется по формуле, мм: b1 = b2 + (5...10). (2.24) Полученное значение ширины округляем до нормального линейного размера. 10. Определим окружную скорость зубчатых колес по формуле, м/с: 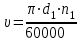 . (2.25) . (2.25)11. По окружной скорости колес с учетом рекомендации табл. 2.6 назначают степень точности зубчатых колес. Таблица 2.6 Нормы точности зубчатых колес
2.3. Проверочный расчет на контактную выносливость активных поверхностей зубьев А. Определение расчетного контактного напряженияКонтактная выносливость устанавливается сопоставлением, действующим в полюсе зацепления расчетного и допускаемого контактного напряжений: 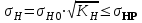 , (2.26) , (2.26)где KH – коэффициент нагрузки; 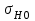 – контактное напряжение в полюсе зацепления при KH = 1. – контактное напряжение в полюсе зацепления при KH = 1.Контактное напряжение в полюсе зацепления при KH = 1 определяют следующим образом, МПа: 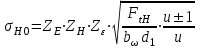 , (2.27) , (2.27)где «+» – для наружного зацепления, «–» – для внутреннего зацепления; 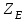 – коэффициент, учитывающий механические свойства материалов сопряженных зубчатых колес. Для стали при модуле упругости – коэффициент, учитывающий механические свойства материалов сопряженных зубчатых колес. Для стали при модуле упругости 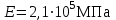 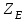 = 190; = 190;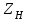 – коэффициент, учитывающий форму сопряженных поверхностей зубьев в полюсе зацепления, – определяют по табл. 2.7. – коэффициент, учитывающий форму сопряженных поверхностей зубьев в полюсе зацепления, – определяют по табл. 2.7.Таблица 2.7 Значения коэффициента 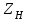
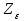 – коэффициент, учитывающий суммарную длину контактных линий; – коэффициент, учитывающий суммарную длину контактных линий;FtH – окружная сила на делительном цилиндре, Н; 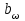 – рабочая ширина венца зубчатой передачи (b2), мм; – рабочая ширина венца зубчатой передачи (b2), мм;d1 – делительный диаметр шестерни, мм. Коэффициент 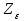 , учитывающий суммарную длину контактных линий, определяется следующим образом: , учитывающий суммарную длину контактных линий, определяется следующим образом: 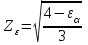 при при 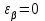 ; ;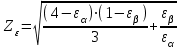 при при 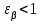 ; (2.28) ; (2.28)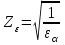 при при 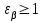 , ,где 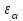 – коэффициент торцевого перекрытия: – коэффициент торцевого перекрытия: 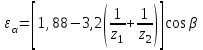 ; ;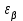 – коэффициент осевого перекрытия: – коэффициент осевого перекрытия: 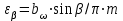 . (2.29) . (2.29)Окружная сила на делительном цилиндре 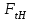 определяется по формуле определяется по формуле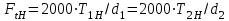 , (2.30) , (2.30)где 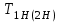 – вращающий момент на шестерне (колесе), Н · м; – вращающий момент на шестерне (колесе), Н · м; 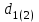 – делительный диаметр шестерни (колеса), мм. – делительный диаметр шестерни (колеса), мм.Коэффициент нагрузки 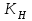 определяют по зависимости определяют по зависимости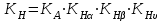 , (2.31) , (2.31)где 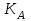 – коэффициент, учитывающий внешнюю динамическую нагрузку (табл. 2.8); – коэффициент, учитывающий внешнюю динамическую нагрузку (табл. 2.8);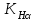 – коэффициент, учитывающий неравномерность распределения нагрузки между зубьями; – коэффициент, учитывающий неравномерность распределения нагрузки между зубьями;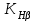 – коэффициент, учитывающий неравномерность распределения нагрузки по ширине зуба; – коэффициент, учитывающий неравномерность распределения нагрузки по ширине зуба;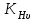 – коэффициент, учитывающий динамическую нагрузку. – коэффициент, учитывающий динамическую нагрузку.Таблица 2.8 Коэффициент внешней динамической нагрузки при расчетах на усталостную прочность 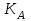
Коэффициент 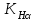 , учитывающий неравномерность распределения нагрузки между зубьями, для косозубых передач определяется по табл. 2.9 в зависимости от окружной скорости и степени точности по нормам плавности. , учитывающий неравномерность распределения нагрузки между зубьями, для косозубых передач определяется по табл. 2.9 в зависимости от окружной скорости и степени точности по нормам плавности.Таблица 2.9 Значения коэффициента 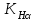
Коэффициент 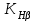 , учитывающий неравномерность распределения нагрузки по длине контактных линий, принимают в зависимости от параметра , учитывающий неравномерность распределения нагрузки по длине контактных линий, принимают в зависимости от параметра 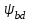 , схемы передачи и твердости активных поверхностей зубьев по графику (определялся ранее по рис. 2.4). , схемы передачи и твердости активных поверхностей зубьев по графику (определялся ранее по рис. 2.4). Коэффициент 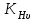 , учитывающий динамическую нагрузку, можно определить по формуле: , учитывающий динамическую нагрузку, можно определить по формуле: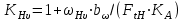 , (2.32) , (2.32)где 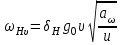 , ,где 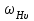 – удельная окружная динамическая сила, Н/мм; – удельная окружная динамическая сила, Н/мм; 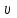 – окружная скорость на делительном цилиндре, м/с. – окружная скорость на делительном цилиндре, м/с.Коэффициент 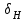 , учитывающий влияние вида зубчатой передачи, модификации профиля головок зубьев, определяется по табл. 2.10. , учитывающий влияние вида зубчатой передачи, модификации профиля головок зубьев, определяется по табл. 2.10.Коэффициент g0, учитывающий влияние разности шагов зацепления зубьев шестерни и колеса, определяется по табл. 2.11. Таблица 2.10 Значения коэффициента 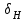
Таблица 2.11 Значения коэффициента 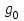
Полученное значение 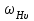 не должно превышать предельного значения не должно превышать предельного значения 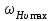 , приведенного в табл. 2.12. В противном случае следует принимать , приведенного в табл. 2.12. В противном случае следует принимать 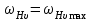 . .Таблица 2.12 Предельные значения 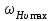
Б. Допускаемые контактные напряжения в проверочном расчетеДопускаемые контактные напряжения 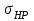 определяют раздельно для шестерни и колеса, МПа: определяют раздельно для шестерни и колеса, МПа: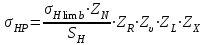 . (2.33) . (2.33)Нахождение значений, входящих в формулу 2.33, рассмотрено при проектировочном расчете за исключением нижеприведенных коэффициентов. Коэффициент 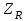 , учитывающий влияние исходной шероховатости сопряженных поверхностей зубьев, определяется по тому из сопряженных колес, зубья которого имеют более грубые поверхности, т. е. в зависимости от параметра шероховатости поверхности (табл. 2.13). , учитывающий влияние исходной шероховатости сопряженных поверхностей зубьев, определяется по тому из сопряженных колес, зубья которого имеют более грубые поверхности, т. е. в зависимости от параметра шероховатости поверхности (табл. 2.13).Таблица 2.13 Коэффициент 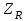 , учитывающий влияние исходной шероховатости , учитывающий влияние исходной шероховатости сопряженных поверхностей зубьев
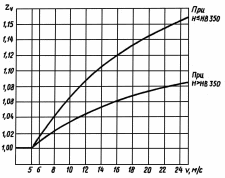
Коэффициент 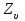 , учитывающий окружную скорость, определяют по графику (рис. 2.7). , учитывающий окружную скорость, определяют по графику (рис. 2.7).
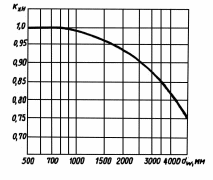
При окружной скорости до 5 м/с 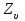 = 1. = 1. Коэффициент 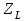 , учитывающий влияние смазки, при отсутствии экспериментальных данных, принимаем , учитывающий влияние смазки, при отсутствии экспериментальных данных, принимаем 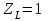 . . Коэффициент 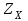 , учитывающий размер зубчатого колеса, в общем случае определяется по кривой, приведенной на рис 2.8. При d < 700 мм следует принимать , учитывающий размер зубчатого колеса, в общем случае определяется по кривой, приведенной на рис 2.8. При d < 700 мм следует принимать 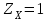 . .
В качестве допускаемого контактного напряжения принимают: – для косозубых передач 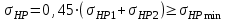 , (2.34) , (2.34)при этом должно выполняться условие: 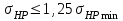 . . При сравнении 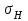 и и 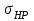 недогруз по контактным напряжениям не должен превышать 20 %. недогруз по контактным напряжениям не должен превышать 20 %. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

 15
15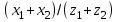
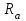 = 1,25…0,63
= 1,25…0,63