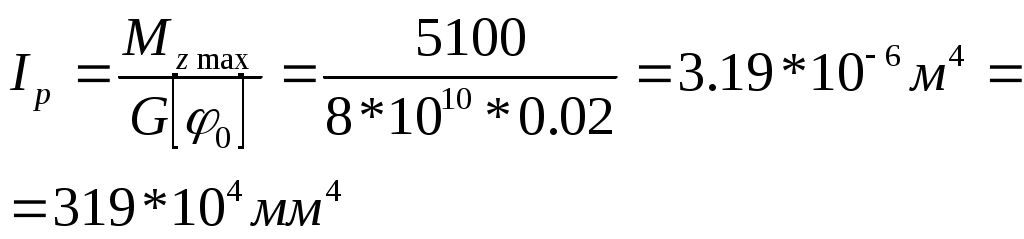Тема построение эпюр продольных сил и нормальных напряжений при растяжении и сжатии, определение перемещений. Расчет на прочность при растяжении и сжатии

• Название: Тема построение эпюр продольных сил и нормальных напряжений при растяжении и сжатии, определение перемещений. Расчет на прочность при растяжении и сжатии
• Дата: 23.01.2022
• Размер: 1.9 Mb.
• Имя файла: Praktika_po_sopromatu_2.doc
• Тип: Практическая работа; #339701

Практические работы

по сопротивлению материалов

Практическая работа.
Тема: построение эпюр продольных сил и нормальных напряжений при растяжении и сжатии, определение перемещений. Расчет на прочность при растяжении и сжатии.

Цель работы: получить практические навыки построения эпюр продольных сил, нормальных напряжений и определения удлинения (укорочения) бруса.

Ход работы:
Теория:

При работе бруса на растяжение и сжатие в его поперечных сечениях возникает только один внутренний силовой фактор (ВСФ) - продольная сила N. Продольная сила в произвольном поперечном сечении бруса численно равна алгебраической сумме проекций на его продольную ось всех внешних сил, действующих на отсеченную часть.

Для расчета на прочность и определения перемещений необходимо знать закон изменения продольных сил по его длине.

Правило знаков: при растяжении продольная сила положительна, при сжатии – отрицательна (рис.10).

Рис. 10

Условие прочности при растяжении (сжатии) имеет вид , где - нормальное напряжение в опасном сечении (т.е. в сечении, где возникают наибольшие напряжения);

N –продольная сила;

А – площадь поперечного сечения;

- допускаемое напряжение.

Исходя из условия прочности, можно решать три вида задач:

1) проверка прочности;

2) подбор сечения А ;

3) определение допустимой нагрузки .

Для нормальных напряжений принимается то же правило знаков, что и для продольных сил.

Изменение длины бруса (удлинение или укорочение) равно алгебраической сумме удлинений (укорочений) его отдельных участков и вычисляется по формуле Гука:
Nili

Δl = ∑ Δli =∑ EAi , где

Ni – продольная сила в пределах каждого участка бруса;

Li - длина отдельного участка бруса;

Ai – площадь поперечного сечения в пределах каждого участка бруса;

Е – модуль продольной упругости материала ( для стали Е=2*10 ⁵ МПа).

Последовательность решения задачи:

1. 
   Разбить брус на участки, начиная от свободного конца. Границами участков являются сечения, в которых приложены внешние силы, а для напряжений также и места изменения размеров поперечного сечения.
   
2. 
   Определить по методу сечений продольную силу для каждого участка (ординаты эпюры N) и построить эпюру продольных сил N. Проведя параллельно оси бруса базовую (нулевую) линию эпюры, отложить перпендикулярно ей в произвольном масштабе получаемые значения ординат. Через концы ординат провести линии, проставить знаки и заштриховать эпюру линиями, параллельными ординатам.
   
3. 
   Для построения эпюры нормальных напряжений определяем напряжения в поперечных сечениях каждого из участков. В пределах каждого участка напряжения постоянны, т.е. эпюра на данном участке изображается прямой, параллельной оси бруса.
   
4. 
   Перемещение свободного конца бруса определяем как сумму удлинений (укорочений) участков бруса, вычисленных по формуле Гука.
   

Пример.
Для данного ступенчатого бруса (рис. 11 , а) построить эпюру продольных сил, эпюру нормальных напряжений и определить перемещение свободного конца, если

Решение:
1. Разбиваем брус на участки, как показано на рис. 11 , а.

2. Определяем ординаты эпюры N на участках бруса:



Строим эпюру продольных сил (рис. 11 , б).

4. Вычисляем значения нормальных напряжений:










Строим эпюру нормальных напряжений (рис. 11, в)
4. Определяем перемещение свободного конца:














Брус удлиняется на 0,23 мм.


Рис. 11

Задача:
Исходя из условия прочности, можно производить три вида расчетов: а) проверочный, при котором проверяется, выполнено ли условие прочности (или ); б) определение допускаемой нагрузки; в) проектный, при котором определяются необходимые размеры поперечных сечений бруса, обеспечивающие заданную прочность. Студенты должны также уметь пользоваться в ходе решения всеми необходимыми формулами, расчетными зависимостями и правильно выполнять вычисления, с учетом указаний к первой задаче второго задания.

Последовательность решения задачи:

1. 
   Брус, равновесие которого рассматривается, освободить от связей и заменить действие связей их реакциями; определить степень статической неопределимости как разность между количеством неизвестных и числом уравнений статики.
   
2. 
   Составить уравнение равновесия; в него войдут обе неизвестные реакции связей, без которых невозможно определить продольные силы, возникающие в брусе или стержне.
   
3. 
   Рассмотреть картину перемещений системы и на основе ее рассмотрения с геометрической точки зрения составить уравнение перемещений, в которое войдут те же неизвестные реакции, что и уравнение статики. Причем перемещения (удлинения или укорочения) участков бруса определяем по формуле Гука .
   
4. 
   Уравнение статики и уравнение перемещений решить совместно и определить искомые реакции связей.
   
5. 
   Определить внутренние силовые факторы (продольные силы) в частях деформируемого бруса или в стержнях или же (если в задаче требуется определить допускаемую нагрузку) выразить продольные силы через искомую нагрузку.
   
6. 
   Произвести заданный в условиях задачи расчет.
   

Рассмотрение ряда конкретных примеров позволит получить представление о методике решения статически неопределимых задач.
Пример:
Для заданного двухступенчатого бруса (рис.12) раскрыть статическую неопределимость, построить эпюры N и по длине бруса, проверить прочность в опасном сечении и вычислить процент перегрузки (недогрузки) бруса, если

Решение:
1. Задача один раз статически неопределима, так как уравнение статики одно ( ), а неизвестных реакций две (рис. 12. а).

2. Составляем уравнение равновесия

(1)

3. Составляем уравнение перемещений. Под действием внешних сил F, R_D, R_B длина бруса вследствие жесткого защемления его концов должна при деформации оставаться неизменной; это условие и используем для составления уравнения перемещений.

Отбросим мысленно нижнюю заделку, заменив ее реакцией R_B (рис. 12, б), получим брус, эквивалентный данному, для которого перемещение сечения В равно нулю:

(2)

Для составления уравнения (2) применен принцип независимости действия сил, т.е. перемещение от совместного действия всех сил равно алгебраической сумме перемещений от действия каждой силы в отдельности. - удлинение участка DC (рис. 12, б) от силы F.

- сумма укорочений участков DC и CB (рис. 12, б) от действия силы /

4. Решая совместно уравнения статики (1) и уравнение перемещений (2), определяем неизвестные реакции R_В и R_D.

Из (2):




Из (1):

5. Определяем внутренние силовые факторы по участкам бруса и строим эпюры продольных сил и нормальных напряжений по длине бруса.



Статическая неопределимость раскрыта – имеем статически определимый брус, заделанный одним концом, нагруженный известными силами F и R_B (рис. 12, б). эпюры продольных сил и нормальных напряжений строим, как для статически определимого бруса (рис. 12, в, г).

6. Наибольшие по абсолютному значению напряжения возникают в поперечных сечениях участка ВС – это опасные сечения.

Определяем процент перегрузки:


а)

б)

г)

R_D

в)


Z



D

2. 
   R_D
   

l 1,5


+

+

1,2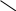A





C

167x10³

133x10³

111


F

A

F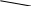

1. 
   R_D
   

l


B

167


Y

R_B

R_B

Рис. 12

ПРАКТИЧЕСКАЯ РАБОТА
Тема: построение эпюр продольных сил и нормальных напряжений при растяжении и сжатии,

Цель работы: получить практические навыки построения эпюр продольных сил, нормальных напряжений
Задачи для практической работы

Двухступенчатый стальной брус, длины ступеней которого указаны на рис. 13 , нагружен силами F₁, F₂, F₃ . Построить эпюры продольных сил и напряжений по длине бруса. Определить перемещение Δl свободного конца бруса, приняв Е=2*10 ⁵ МПа. Числовые значения F₁, F₂, F_{3 и} площади поперечных сечений ступеней А₁ и А₂ для своего варианта взять из таблицы 4.


Таблица 4

Вариант	Схема на рис.	F1 кН	F2 кН	F3 кН	A1 См2	A2 См2
1	10	30	10	5	1,8	3,2
2	9	16	15	10	1,1	1,8
3	8	17	13	8	1,0	2,2
4	7	14	16	11	1,2	1,9
5	6	27	14	8	1,7	3,1
6	5	24	11	6	1,5	2,9
7	4	18	12	5	1,6	2,8
8	3	26	13	7	1,7	3,1
9	2	36	20	12	2,5	4,0
10	1	32	16	9	1,0	2,2

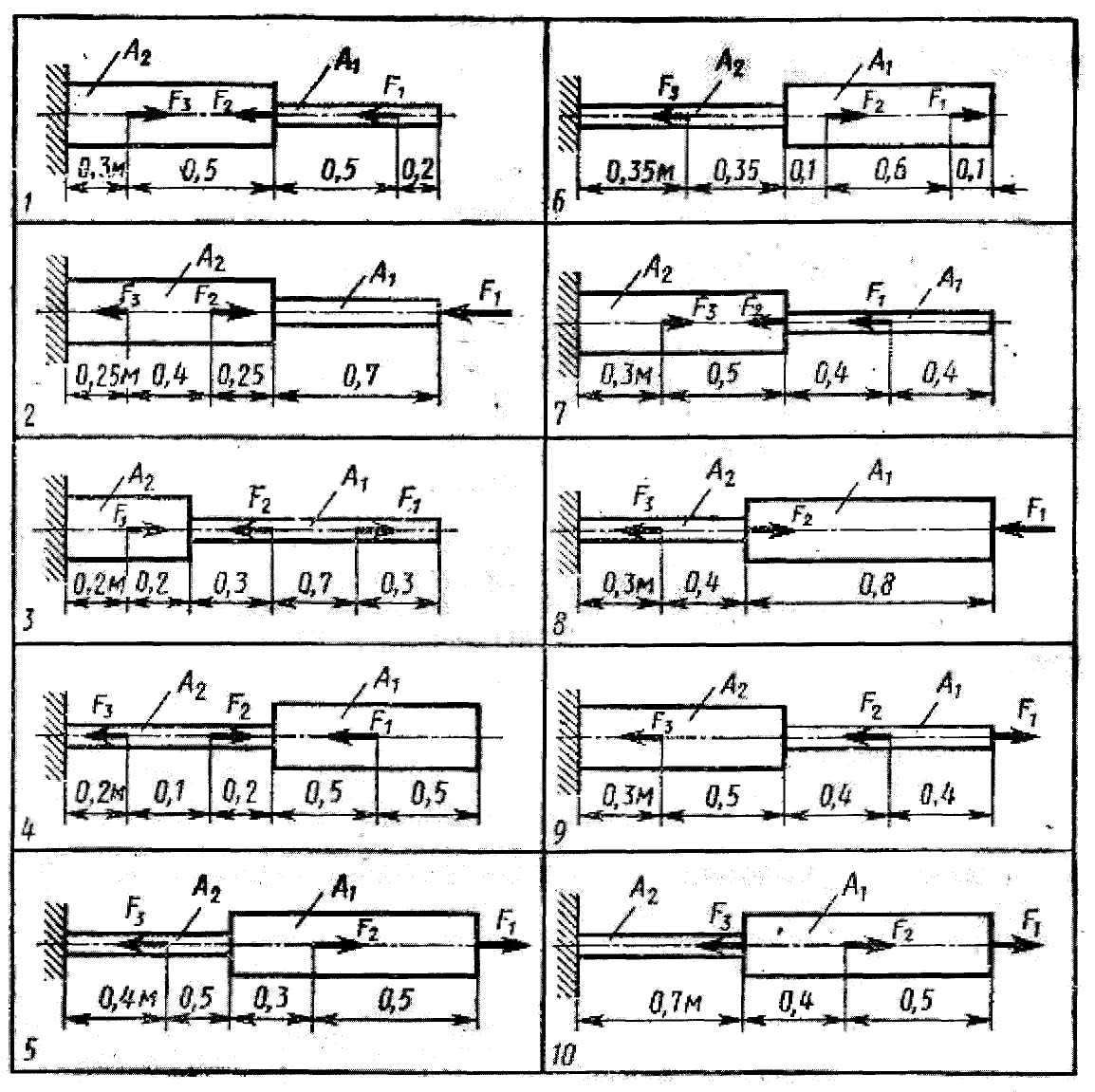Рис. 13


Практическая работа.
Тема: построение эпюр крутящих моментов и определение диаметра вала из условия прочности и жесткости при кручении.

Цель работы: получить практические навыки построения эпюры крутящих моментов и касательных напряжений, выполнить расчеты на прочность и жесткость.

Ход работы:
Теория:

Кручением называют такой вид нагружения бруса, при котором в его поперечных сечениях возникает только один внутренний силовой фактор – крутящий момент М_КР (или М_Z).

Крутящий момент в произвольном поперечном сечении бруса равен алгебраической сумме внешних моментов, действующих на отсеченную часть: М_КР = (имеется в виду, что плоскости действия всех внешних скручивающих моментов перпендикулярны продольной оси бруса).

Будем считать крутящий момент положительным, если для наблюдателя, смотрящего на проведенное сечение, он представляется направленным по часовой стрелке, отрицательным , если внешний момент направлен против часовой стрелки (рис. 14 ).



Рис.14

В задаче необходимо выполнить проектный расчет вала круглого поперечного сечения из условий прочности и из условий жесткости; из двух полученных значений диаметров следует выбрать наибольшее значение.

Последовательность решения задачи:

1. Определить внешние скручивающие моменты по формуле , где P – мощность, - угловая скорость.

2. Определить уравновешивающий момент, используя уравнение равновесия , так как при равномерном вращении вала алгебраическая сумма приложенных к нему внешних скручивающих (вращающих) моментов равна нулю.

3. Пользуясь методом сечений, построить эпюру крутящих моментов по длине вала.

4. Для участка вала, в котором возникает наибольший крутящий момент, определить диаметр вала для круглого сечения из условий прочности и жесткости.

Из условия прочности: . Здесь , где - наибольший крутящий момент : -полярный момент сопротивления кручению; - допускаемое касательное напряжение. Учитывая, что для круглого сечения , и используя условие прочности, можно получить уравнение , откуда определяется необходимый по прочности диаметр поперечного сечения вала:

Из условия жесткости: Здесь , где - полярный момент инерции сечения; G – модуль упругости при сдвиге; - допускаемый угол закручивания сечения. Учитывая, что для круглого сечения , и используя условие жесткости, можно получить уравнение: , откуда определяется необходимый по жесткости диаметр поперечного сечения вала:

Из двух поперечных диаметров вала выбрать наибольший.
Пример:
Для стального вала (рис. 15 ) круглого поперечного сечения постоянного по длине (рис.15, а) требуется:

1. Определить значения моментов М₂ и М₃, соответствующие передаваемым мощностям Р₂ и Р₃, а также уравновешивающий момент М₁.

2. Построить эпюру крутящих моментов.

3. Определить требуемый диаметр вала из расчетов на прочность и жесткость, если

окончательное значение диаметра округлить до ближайшего четного (или оканчивающего на пять) числа.
Решение:
1. Определяем величины внешних скручивающих моментов М₂ и М₃:
.
2. Определяем уравновешивающий момент М₁:


3. Строим эпюру М_z (рис.15, б).
4. Определяем диаметр вала из условий прочности и жесткости. (рис.15, б).

Из условия прочности: где принимаем d = 95 мм

, где принимаем d = 76 мм.

Требуемый размер сечения получился больше из расчета на прочность, поэтому его принимаем как окончательный: d = 95 мм.


Рис.15

Задачи для практической работы

Для стального вала постоянного поперечного сечения (рис. 16): 1) определить значения моментов М1, М2, М3; 2) построить эпюру крутящих моментов; 3) определить диаметр вала из расчетов на прочность и жесткость. Приняв 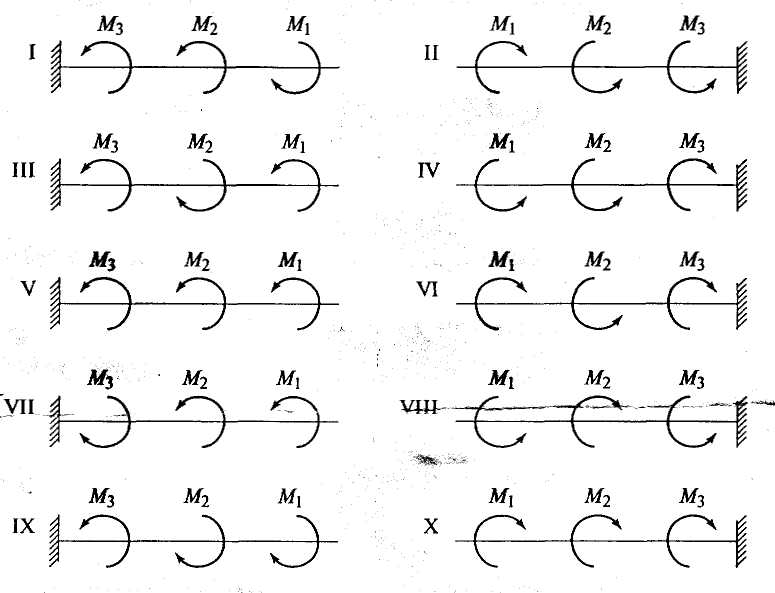=30 МПа; =0,02 рад/м. Данные своего варианта взять из табл. 5. Окончательное значение диаметра вала должно быть округлено до ближайшего четного или оканчивающегося на пять числа.



Рис. 16

Таблица 5

Варианты	Схема на рис	М1, кН∙м	М2, кН∙м	М3, кН∙м
1,11,21	1	0,9	1,5	1,5
2, 12,21	2	2,5	1,3	0,8
3,13,23	3	1,1	0,7	3,2
4,14,24	4	0,8	1,4	0,7
5,15,25	5	4,2	2,0	1,2
6,16,26	6	1,3	1,3	0,7
7,17,27	7	14,5	1,4	0,9
8,18,28	8	1,2	0,9	4,0
9,19,29	9	1,9	2,0	0,6
10,20,30	10	3,0	1,0	1,9

ПРАКТИЧЕСКАЯ РАБОТА
Тема работы: Построение эпюр поперечных сил и изгибающих моментов. Расчеты на прочность при изгибе.

Цель работы: получить практические навыки построения эпюр поперечных сил и изгибающих моментов, выполнять проектировочный расчет балки ни изгиб

Ход работы:
Теория:

Изгиб – это такой вид нагружения балки, при котором в ее поперечных сечениях возникают изгибающие моменты. В большинстве случаев одновременно с изгибающими моментами возникают и поперечные силы; такой изгиб называют поперечным. Если поперечные силы не возникают, изгиб называют чистым.

Изгибающий момент в произвольном сечении равен алгебраической сумме моментов внешних сил, действующих на оставленную часть балки:

М_и = ∑М_о (Fi)

Поперечная сила Q_у равна алгебраической сумме проекций внешних сил, действующих на оставленную часть балки:

Q_у = ∑ F_iу
Правило знаков для внешних сил: силам, поворачивающим относительно сечения оставленную часть балки по ходу часовой стрелки, приписывается знак плюс, а силам, поворачивающим относительно сечения оставленную часть балки против хода часовой стрелки, приписывается знак минус (рис.17 )



Рис.17

Правило знаков для внешних моментов: внешним моментам, изгибающим ось балки выпуклостью вниз, приписывается знак плюс, а моментам, изгибающим ось балки выпуклостью вверх, - знак минус (рис.18 ).



Рис.18

Для балок, имеющих много участков нагружения. Эпюры изгибающих моментов Ми строятся по характерным точкам, т.е. по точкам, в которых приложены внешние моменты и силы.

Между выражениями изгибающего момента М_и, поперечной силы Q_у и интенсивностью распределенной нагрузки q существуют дифференциальные зависимости:

d М_и = dQ_у = q

dz dz

На основе метода сечений и дифференциальных зависимостей устанавливается взаимосвязь эпюр М_и и Q_у между собой и с внешней нагрузкой, поэтому достаточно вычислить ординаты эпюр для характерных сечений и соединить их линиями.

Правила построения эпюр:

Для эпюры поперечных сил:

1. 
   На участке, нагруженном равномерно распределенной нагрузкой. Эпюра изображается прямой, наклоненной к оси балки.
   
2. 
   На участке, свободном от распределенной нагрузки. Эпюра изображается прямой. Параллельной оси балки.
   
3. 
   В сечении, где приложена сосредоточенная пара сил, поперечная сила не изменяет своего значения.
   
4. 
   В сечении, где приложена сосредоточенная сила, эпюра поперечных сил меняется скачкообразно на значение, равное приложенной силе.
   
5. 
   В концевом сечении балки поперечная сила численно равна сосредоточенной силе (активной или реактивной), приложенной в этом сечении. Если в концевом сечении балки не приложена сосредоточенная сила, то поперечная сила в этом сечении равна нулю.
   

Для эпюры изгибающих моментов:

1. 
   На участке, нагруженном равномерно распределенной нагрузкой, эпюра моментов изображается квадратичной параболой. Выпуклость параболы направлена навстречу нагрузке.
   
2. 
   На участке, свободном от равномерно распределенной нагрузки, эпюра моментов изображается прямой линией.
   
3. 
   В сечении балки. где приложена сосредоточенная пара сил. Изгибающий момент меняется скачкообразно на значение, равное моменту приложенной пары.
   
4. 
   Изгибающий момент в концевом сечении балки равен нулю, ли в нем не приложена сосредоточенная пара сил. Если же в концевом сечении приложена активная или реактивная пара сил, то изгибающий момент в этом сечении равен моменту приложенной пары.
   
5. 
   На участке, где поперечная сила равна нулю. Балка испытывает чистый изгиб, и эпюра изгибающих моментов изображается прямой, параллельной оси балки.
   
6. 
   Изгибающий момент принимает экстремальное значение в сечении, где эпюра поперечных сил проходит через нуль, меняя знаки с «+» на «--» или с «--» на «+» .
   

Условие прочности для балок с сечениями, симметричными относительно нейтральной оси, имеет вид: M_{и max}

σ_max = W_x ≤ [σ] ,

где W_{x –} осевой момент сопротивления сечения .

Для подбора сечения балки (проектного расчета) из условия прочности определяют необходимое значение осевого момента сопротивления:

W_x ≥ M _{и max} / [σ]
Для определения опорных реакций балки используются уравнений равновесия:

∑F_ix = 0

∑F_iy = 0

∑M_o( Fi) = 0
Последовательность решения задачи:

1. 
   Балку разделить на участки по характерным точкам.
   
2. 
   Определить опорные реакции балки, исходя из условия равновесия.
   
3. 
   Определить вид эпюры поперечных сил на каждом участке в зависимости от внешней нагрузки, вычислить поперечные силы в характерных сечениях и построить эпюру поперечных сил.
   
4. 
   Определить вид эпюры изгибающих моментов на каждом участке в зависимости от внешней нагрузки, вычислить изгибающие моменты в характерных сечениях и построить эпюру изгибающих моментов. Для определения экстремальных значений изгибающих моментов дополнительно определить моменты в сечениях, где эпюры поперечных сил проходят через нуль.
   
5. 
   для подбора сечения из условия прочности определить W_x в опасном сечении, т.е. в сечении, где изгибающий момент имеет наибольшее по модулю значение.
   

Пример. Для заданной двухопорной балки (рис.19) определить реакции опор, построить эпюры поперечных сил и изгибающих моментов, определить размеры поперечного сечения (h, b, d) в форме прямоугольника и круга, приняв для прямоугольника h/ b=1,5. Считать [σ]=160 МПа. Дано: F₁=18кН, F₂=30кН, М₁=20 кНм, М₂=10кНм.

Решение. 1. Строим расчетно-графическую схему (рис19,б.)



Рис. 19

2. Определяем опорные реакции балки R_Bx , R_By, R_D и проверяем их найденные значения.
∑M_D = 0; ∑M_D = - M₁ + F₂ CD + M₂ + R_BY BD – F₁ OD = 0 ;

M₁ – F₂ CD – M2 + F₁ OD 20 – 30*6 – 10 + 18*15

R_BY = BD = 10 = 10 kH;
∑M_B = 0; ∑M_B = - F₁ OB + M₂ – F₂ BC – R_D BD – M₁ =0;

- F₁ OB + M₂ – F₂ BC – M₁ -18*5 + 10 – 30*4 – 20

R_BY = BD = 10 = - 22 kH;

∑F_ix = 0; R_BХ = 0
Так как реакция R_D получилась со знаком минус. То изменяем ее первоначальное направление на противоположное. Истинное направление реакции R_D - вниз (рис. 19, б).

Проверка: ∑F_iy = 0

- F₁ + R_BY + F2 - R_D =0

- 18 + 10 + 30 – 22 = 0

- 40 + 40 = 0

Условие равновесия статики выполняется, следовательно, реакции опор балки найдены правильно:
R_BХ = 0, R_BY = 10 кН, R_BY = 22 кН.

3. 
   Определяем поперечные силы Q_Y в характерных точках: О, В, С, D и строим эпюру слева направо ( рис. 19, в):
   

Q_О = - F₁ = - 18 kH,

Q_{B слева} = - F₁ = - 18 kH,

Q_{B справа} = - F₁ + R_By= - 18 + 10 = - 8 kH,

Q_{C слева} = - F₁ + R_By = - 18 + 10 = - 8 kH,

Q_{C справа} = - F₁ + R_{By +} F₂ = - 18 + 10 + 30 = 22 kH

Q_{D слева} = - F₁ + R_{By +} F₂ = - 18 + 10 + 30 = 22 kH

3. 
   Вычисляем изгибающие моменты к тех же характерных точках: О, В, С, D и строим эпюру М_и (рис. 19, г):
   

М_{и О} = 0,

М_{и В} = - F1 OB = - 90 kH м,

М_{и C слева} = - F₁ OC + R_BY BC = - 18 * 9 + 10 * 4 = - 122 kH м,

М_{и C справа} = - F₁ OC + R_BY BC – M₂ = - 18 * 9 + 10 * 4 + 10 = - 112 kH м,

М_{и D} = - F₁ OD + R_BY BD – M₂ + F₂ CD = - 18 * 15 + 10 * 10 + 10 + 30 * 6 = 20 kH м

3. 
   Вычисляем размеры сечений данной балки по двум вариантам:
   

а) сечение – прямоугольник с заданным соотношением сторон;

б) сечение – круг.

Вычисляем размеры прямоугольного сечения из условий прочности на изгиб

M_{и max}

σ_max = W_x ≤ [σ] ,
Максимальный изгибающий момент берется в точке С слева М_{и max} = 122 kH м

Осевой момент для прямоугольного сечения

W_x = = =

Так как h/b = 1,5, h = 1,5 b.

Тогда

M_{и max}* 6

σ_max = 2,25 b ³ ≤ [σ] ,

Отсюда

b ≥ = = 127 мм.

(1кН м = 10 ⁶ Н мм).

Так как b = 127 мм, то h = 1,5 b = 1,5 * 127 = 190,5 мм.

Вычисляем размер круглого сечения из условия прочности на изгиб

M_{и max}

σ_max = W_x ≤ [σ] ,
Так как для круга W_x = = 0,1 d³, то

σ_и = ≤ [σ_и]

Отсюда находим диаметр сечения:
d ≥ = =195 мм

Ответ: b = 127 мм, h = 190,5 мм, d = 195 мм.

Задачи для практической работы
Для заданной двухопорной балки (рис. 20) определить реакции опор, построить эпюры поперечных сил и изгибающих моментов. Подобрать из условия прочности на изгиб размеры поперечного сечения прямоугольника или круга, приняв для прямоугольника h=2b. Считать [σ_и]= 150 Мпа.

Данные для различных вариантов указаны в табл. 6.

Таблица 6

Варианты	Схема на рис.20	F1, кН	F2, кН	М, кН м
1, 11, 21	1	20	10	12
2, 12, 22	2	12	8	20
3, 13, 23	3	10	15	30
4,14,24	4	30	20	40
5, 15,25	5	18	22	35
6,1 6, 26	6	16	24	45
7, 17, 27	7	15	10	8
8, 18, 28	8	8	14	6
9, 19, 29	9	4	10	12
10, 20, 30	10	5	8	3

Рис. 20