поверхности и тела. 007. Поверхности и тела. Тема Поверхности и тела
 Скачать 137.57 Kb. Скачать 137.57 Kb.
|
Тема 2.3. Поверхности и телаПРЯМОУГОЛЬНЫЕ ПРОЕКЦИИ ГЕОМЕТРИЧЕСКИХ ТЕЛ Форма большинства предметов представляет собой сочетание различных геометрических тел или их частей. Следовательно, для чтения чертежей необходимо знать, как изображаются геометрические тела. Проекции призмыНа рис. 2.38 изображена прямая правильная треугольная призма. Призмойназывается многогранник, у которого основания – равные многоугольники с соответственно параллельными сторонами. Боковые грани призмы - параллелограммы. Если ребра боковых граней перпендикулярны основанию, то призму называют прямой. Для задания призмы достаточно задать одно ее основание и боковое ребро. У прямой призмы все грани будут являться проецирующими плоскостями.  Рис. 2.38 Точка принадлежит поверхности, если она принадлежит какой-нибудь линии, принадлежащей поверхности. Линия принадлежит поверхности, если она проходит через точки, принадлежащие поверхности. На рисунке 2.39 показаны две проекции прямой призмы.  ·  Точка М заданная проекцией m’ принадлежит поверхности призмы. Нужно найти горизонтальную проекцию точки М. Так как грань BC представляет собой проецирующую плоскость, следовательно, все точки расположенные в этой грани будут расположены на линии основания призмы bc (рисунок 2.39). Проекции пирамиды Пирамида представляет собой многогранник, у которого одна грань - основание (произвольный многоугольник ABCD). Остальные грани (боковые) - треугольники с общей вершиной S, называемой вершиной пирамиды. Для задания на чертеже пирамиды достаточно задать ее основание и вершину. На рис. 2.40 показаны две проекции прямой пирамиды. 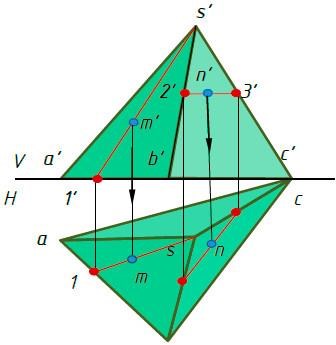 Рис. 2.40 Чтобы построить проекции точки на поверхности пирамиды, нужно через эту точку провести прямую. Например, если задана фронтальная проекция точки М, принадлежащей грани SAB, то для построения горизонтальной проекции нужно через эту точку провести прямую S1. Также через точку N заданную фронтальной проекцией мы проводим прямую 2–3 параллельную стороне треугольника основания пирамиды BC. Находим горизонтальную проекцию прямой 2−3, а затем определяем недостающую горизонтальную проекцию точки N. Проекции цилиндра Цилиндромназывается тело, которое состоит из двух кругов, совмещаемых параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих кругов. Круги называются основаниями цилиндра, а отрезки, соединяющие соответствующие точки окружностей кругов, – образующими цилиндра. На рис. 2.41 изображен цилиндр. Круги с центрами О и О1 являются его основаниями, АА1, BB1, СС1 – его образующие. Цилиндр называется прямым, если его образующие перпендикулярны плоскостям оснований. На рис. 2.42 изображен наклонный цилиндр. Радиусом цилиндра называется радиус его основания. Высотой цилиндра называется расстояние между плоскостями оснований. Осью цилиндра называется прямая, проходящая через центры оснований. 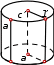 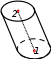 Рис. 2.41 Рис. 2.42 Проекции конуса Конусом называется тело, которое состоит из круга – основанияконуса, точки, не лежащей в плоскости этого круга, – вершины конуса и всех отрезков, соединяющих вершину конуса с точками основания. Отрезки, соединяющие вершину конуса с точками окружности основания, называют образующими конуса. Поверхность конуса состоит из основания и боковой поверхности. На рис. 2.43 изображен круговой конус. S – вершина конуса, круг с центром в точке О – основание конуса, SA, SB, SC – образующие конуса.  Рис. 2.43 Конус называется прямым, если прямая, соединяющая вершину конуса с центром основания, перпендикулярна плоскости основания. Проекции шара Шаром называется тело, которое состоит из всех точек пространства, находящихся на расстоянии, не большем данного, от данной точки. Эта точка называется центром шара, а данное расстояние – радиусомшара. На рисунке 5.44 изображен шар с центром в точке О и радиусом R. 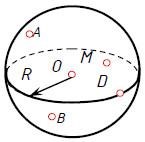 Рис. 2.44 Точки А, В, М и О принадлежат данному шару. Граница шара называется шаровой поверхностью или сферой. Отрезок, соединяющий две точки шаровой поверхности и проходящий через центр шара, называется диаметром. Концы любого диаметра называются диаметрально противоположными точками шара. Шар образуется при вращении полукруга вокруг его диаметра как оси. Плоскость, проходящую через ось поверхности вращения, называют меридиальной. Линию ее пересечения с поверхностью – меридианом. Меридиан, параллельный фронтальной плоскости проекций, называютглавным меридианом(рис. 2.45). Наибольшая окружность, лежащая в плоскости, перпендикулярной оси вращения называется экватором. 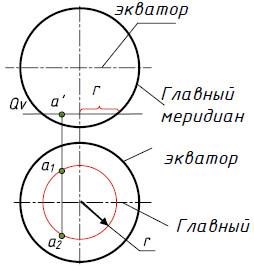 Рис. 2.45 Критерии оценивания урока
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
