финансовая математика. финансовая математика тест. Тема Простые проценты

• Название: Тема Простые проценты
• Анкор: финансовая математика
• Дата: 30.09.2022
• Размер: 195.28 Kb.
• Имя файла: финансовая математика тест.docx
• Тип: Документы; #707371
• страница: 1 из 4

Тема 1. Простые проценты

1. Процентная ставка – отношение суммы процентных денег, выплачиваемых за определенный период к некоторому базовому капиталу. Рассчитывается

а) отношением дохода к величине капитала

б) отношением капитала к величине дохода

в) отношением дохода к периоду сделки

г) отношением периода сделки к доходу

Ответ А

2. Наращенная сумма это первоначальный капитал плюс проценты (ответ в)

а) процентные деньги

б) сумма авансированного капитала

в) сумма долга плюс проценты

г) все ответы верны

Ответ В

3. Если срок финансовой сделки не равен целому числу лет, наращенная сумма определяется (проценты простые)

а) S=P(R i)^п

б) S = P(l+n*i)

в) S = P(l*t/K*i)

г) S = P(l+t*K*i)

Ответ Б

4. При французском методе (а)

а) число дней - точное, продолжительность года - 360 дней

б) число дней - точное, продолжительность года - 365 дней

в) число дней — исходя из продолжительности месяцев -30 дней, продолжительность года - 360 дней

г) число дней - приближенное, продолжительность года - 365 дней

Ответ А

5. Учетная ставка применяется при (в)

а) декурсивном методе

б) антисипативном методе

в) дисконтировании

г) все ответы верны

Ответ В

6. I= Р* п * i - это формула (а)

а) простых процентов

б) процентного дохода

в) дисконтирования

г) все ответы верны

Ответ А

7. Номинальная ставка процентов используется, если

а) используется сложная ставка процентов

б) используется простая ставка процентов

в) начисление сложных процентов производится несколько раз в году

г) начисление простых процентов производится несколько раз в год

Ответ Б

8. Что означает принцип финансовой неравноценности денег, относящихся к различным моментам времени?

а) обесценение денег в связи с инфляцией;

б) возрастание риска с увеличением срока ссуды;

в) возможность инвестировать деньги с целью получить доход;

г) снижение себестоимости товаров в связи с научно-техническим прогрессом.

9. Проценты начисляются на одну и ту же величину капитала при (б)

а) сложных процентах

б) простых процентах

в) простых и сложных процентах

г) все ответы верны

Ответ Б

10. Математическое дисконтирование осуществляется на основе

а) процентной ставки

б) учетной ставки

в) ставки рефинансирования

г) все ответы верны

Ответ Б

11. Укажите возможные способы измерения ставок процентов

а) только процентами;

б) только десятичной дробью;

в) только натуральной дробью с точностью до 1/32;

г) процентами, десятичной или натуральной дробью.

12. Укажите формулу наращения по простым процентам.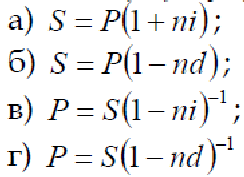



Ответ А

13.В чем сущность французской практики начисления простых процентов?

а) в использовании обыкновенных процентов и приближенного срока ссуды;

б) в использовании точных процентов и приближенного срока ссуды;

в) в использовании точных процентов и точного срока ссуды;

г) в использовании обыкновенных процентов и точного срока ссуды.

14.В чем сущность германской практики начисления простых процентов?

а) в использовании обыкновенных процентов и приближенного срока ссуды;

б) в использовании точных процентов и приближенного срока ссуды;

в) в использовании точных процентов и точного срока ссуды;

г) в использовании обыкновенных процентов и точного срока ссуды.

15. В чем сущность британской практики начисления простых процентов?

а) в использовании обыкновенных процентов и приближенного срока ссуды;

б) в использовании точных процентов и приближенного срока ссуды;

в) в использовании точных процентов и точного срока ссуды;

г) в использовании обыкновенных процентов и точного срока ссуды.

16. Укажите формулу расчета наращенной суммы, когда применяется простая ставка, дискретно изменяющаяся во времени.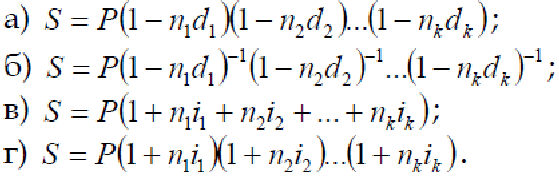



Ответ В

17. Укажите формулу расчета наращенной суммы в операции с реинвестированием под дискретно изменяющуюся простую ставку процентов.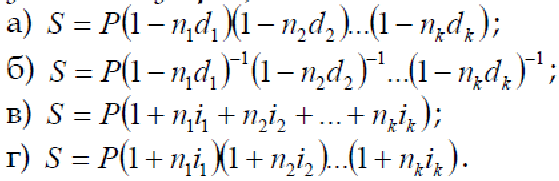



Ответ Г.

18.Укажите формулу математического дисконтирования в случае применения простой процентной ставки.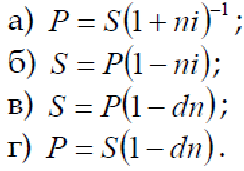



Ответ А.

19.Укажите формулу банковского учета по простой процентной ставке.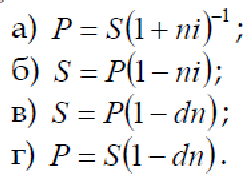



Ответ Г.

20. Процесс дисконтирования:

а) по заданной исходной сумме и процентной ставке необходимо найти ожидаемую к получению сумму;

б) по заданной ожидаемой в будущем к получению суммы и процентной ставке необходимо найти исходную сумму долга;

в) расчет доходности;

г) нет верного ответа.

Ответ Б.

Тема 2. Сложные проценты

1. Укажите формулу, по которой вычисляется срок удвоения первоначальной суммы при применении сложных процентов.



Ответ Б.

2. Укажите формулу наращения по сложным процентам.



Ответ В.

3. Как вычисляется наращенная сумма при применении сложных процентов, если ставка дискретно меняется во времени.





Ответ В.

4. Укажите формулу математического дисконтирования по сложной ставке.



Ответ А.

5. Укажите формулу банковского учета по сложной учетной ставке.



г) 

Ответ Г.

6. Какая из формул верно определяет сложную учетную ставку?



Ответ В.

7. Какая из формул верно определяет сложную ставку?



Ответ Б.

8. Какая из формул верно определяет номинальную сложную учетную ставку?



Ответ Б.

9. Какая формула верно отражает связь между сложной номинальной учетной ставкой и сложной годовой учетной ставкой?



Ответ Г.

10. Какая формула верно определяет силу роста?



Ответ В.

11. Наращенная сумма сложных процентов при использовании учетной ставки

рассчитывается:

а) S = P(1+ i)^п

б)-S = P/ (l-n*d)

в) S = P/(l-d)^п

г) S = P(l+n*i)

Ответ А.

12. Капитализация процентов – это:

а) величина дохода за фиксированный интервал времени;

б) доход от предоставления денег в долг в любой форме;

в) присоединение начисленных процентов к основной сумме;

г) все ответы верны.

Ответ В.

13. Реинвестирование:

а) многоразовое наращение; 

б) одноразовое наращение;

в) наращение один раз;

г) нет верного ответа.

Ответ А.

14. Арифметическая прогрессия соответствует:

а) дисконту;

б) наращению;

в) сложным процентам;

г) простым процентам.

Ответ Г.

15. База для начисления сложных процентов:

а) меняется за счет присоединения ранее начисленных процентов;

б) не меняется;

в) меняется за счет внешних факторов;

г) меняется за счет внутренних факторов.

Ответ А.

16. Присоединение начисленных процентов к сумме долга, которая служит базой для их начисления, – это:

а) капитализация процентов;

б) доход процентов;

в) изменение процентов;

г) все ответы верны.

Ответ А.

17. Период начисления – это:

а) интервал времени получения дохода;

б) процесс накопления денежной суммы вклада;

в) интервал времени, к которому приурочена процентная ставка;

г) все ответы верны.

Ответ А.

18. Период начисления для сложных ставок ссудного процента:



Ответ 3.

19. Множитель (коэффициент) наращения определяется как:

а) величина, показывающая во сколько раз вырос первоначальный капитал;

б) отношение наращенной суммы к первоначальному капиталу;

в) отношение процентных денег к наращенной сумме;

г) величина, показывающая во сколько раз вырос первоначальный капитал по сравнению с начисленным доходом.

Ответ А, Б.

20. Величина, обратная коэффициенту наращения:

а) коэффициент дисконтирования;

б) коэффициент прироста;

в) коэффициент наращения;

г) первоначальный капитал;

д) наращенная сумма.

Ответ А.

Тема 3. Эквивалентность процентных ставок

1. Ставки, обеспечивающие равноценность финансовых последствий, называются:

а) декурсивными;

б) антисипативными;

в) номинальными;

г) эквивалентными.

Ответ Г.

2. Для определения эквивалентных процентных ставок необходимо знать:

а) какой инструмент требуется для корректного сравнения различных процентных ставок;

б) существует ли возможность выбора условий финансовой операции;

в) реальный относительный доход в целом за год.

Ответ А.

3. Два платежа считаются эквивалентными, если:

а) равны процентные ставки;

б) приведенные к одному моменту времени они оказываются равными;

в) равны наращенные суммы;

г) равны учетные ставки.

Ответ Б.

4. Консолидирование платежей это:

а) объединение платежей;

б) замена платежей;

в) разность наращенных сумм;

г) разность дисконтных платежей.

Ответ А.

5. Принцип финансовой эквивалентности состоит в том, что:

а) процентные ставки одинаковые;

б) учетные ставки одинаковые;

в) неизменность финансовых отношений участников до и после изменения финансового соглашения;

г) сложные учетные ставки равны.

Ответ В.

6. При использовании сложных процентов расчет приведенных стоимостей при замене платежей можно осуществлять:

а) на любой момент времени;

б) на момент заключения контракта;

в0 на начальный момент;

г) на момент времени по договоренности.

Ответ Г.

7. Имеются два обязательства. Условие первого: выплатить 400 рублей через четыре месяца; условие второго: выплатить 450 рублей через 8 месяцев. Барьерная процентная ставка (при простой процентной ставке 20%) равна:

а) 40,5%;

б) 41%;

в) 42,8%;

г) 45%.

Ответ Б.

8. Два платежа 1 и 2 млн. рублей и сроками уплаты через 2 и 3 года объединяются в один. Укажите точный срок консолидированного платежа в сумме 3 млн. руб. Используется сложная ставка 20%.

а) 1,12 года;

б) 1,35 года;

в) 1,5 года;

г) 1,646 года.

Ответ Г.

9. Два платежа 1 и 2 млн. рублей и сроками уплаты через 2 и года объединяются в один. Определить приближенный срок консолидированного платежа в сумме 3 млн. рублей. Используется сложная ставка 20%.

а) 2,646 года;

б) 2,5 лет;

в) 2,72 года;

г) 1,646 года.

Ответ Г.

10. Платеж в 5 тыс. рублей сроком уплатить 4 месяца, заменить платежом со сроком уплаты 3 месяца. Использовать простую процентную ставку 10%.

а) l4,5 тыс. рублей;

б) 4,959 тыс. рублей;

в) 5,51 тыс. рублей;

г) 6,7 тыс. рублей.

Ответ Б.

11. Для одних и тех же условий номинальная учетная ставка:

a) больше эффективной;

б) меньше эффективной;

в) равна эффективной;

г) нет верного ответа.

Ответ Б.

12. Эффективная ставка — это такая годовая номинальная ставка
а) простых процентов, которая дает возможность получить тот же результат, как и при б) начислении процентов несколько раз в году
в)сложных процентов, которая дает возможность получить тот же результат, как и при начислении процентов несколько раз в году

Ответ В

13. Эквивалентные проценты ставки это:

а) такие процентные ставки разного вида привлечения, которых при одинаковых начальных условиях дают одинаковые проценты;

б) сумму дисконта;

в) наращенную сумму;

г) современную величину;

д) финансовые результаты.

Ответ А

14. Средние сложные проценты ставки определяются по формуле:

а) средний гармонический;

б) средний арифметический простой;

в) средний арифметический взвешенный; г) средний геометрический взвешенный.

Ответ Г

15. Эквивалентными считаются платежи, если они приведены к одному моменту времени по заданной процентной ставке путем:

а) наращения;

б) дисконтирования;

в) определения покупательной способности;

г) индексирования.

Ответ Б

16. При составлении уравнения эквивалентности обязательно нужно выбрать:

а) период начисления процентов;

б) базовую дату;

в) количество интервалов начисления процентов.

Ответ А,В

17. Консолидировать платежи можно путем:

а) наращения по простой процентной ставке;

б) наращения по простой учетной ставке;

в) наращения по сложной процентной ставке;

г) определения срока консолидированного платежа.

Ответ Г

18. Учет инфляции в финансовых расчетах требует: а) индексации первоначальной суммы;

б) корректировки процентной ставки;

в) изменения периода начисления процентов;

г) изменение интервалов начисления процентов.

Ответ Б

19. «Инфляционная премия» это:

а) добавление к реальной ставке прироста инфляции;

б) добавления к реальной ставке прироста инфляции и произведения ставки на прирост инфляции;

в) умножения реальной ставки на темп инфляции; г) деления реальной ставки на темп инфляции.

Ответ Б

20. Какие источники дохода наиболее вероятны при конверсии валюты: а) наращения процентов;

б) изменение курса;

в) комиссионные;

г) все перечисленные выше источники одновременно.

Ответ Г

Тема 4. Рентные платежи и их анализ.

1. Что такое рента постнумерандо?

а) рента, образуемая платежами после некоторого указанного момента времени;

б) рента, платежи которой поступают в конце каждого периода;

в) рента, платежи которой скорректированы с учетом инфляции;

г) рента, платежи которой скорректированы на величину налога.

2. Что такое рента пренумерандо?

а) рента, образуемая платежами до некоторого указанного момента времени;

б) рента, платежи которой поступают в начале каждого периода;

в) рента, платежи которой поступают до корректировки на инфляцию;

г) рента, платежи которой поступают до корректировки на величину налога.

3. Что такое р-срочная рента?

а) рента со сроком р лет;

б) рента с периодом начисления процентов р лет;

в) рента с р платежами в году;

г) рента с р начислениями процентов в году.

4. Как связаны между собой современная величина и наращенная сумма ренты?



Ответ А.

5. Укажите коэффициент наращения обычной годовой ренты при однократном начислении процентов в году.



Ответ А.

6. Укажите коэффициент приведения обычной годовой ренты при однократном начислении процентов в году.



Ответ Б.

7. Укажите коэффициент наращения обычной p – срочной ренты при m – кратном начислении процентов в году в общем случае.



Ответ А.

8. Укажите коэффициент приведения обычной p – срочной ренты при m – кратном начислении процентов в году в общем случае.





Ответ Б.

9. Укажите формулу определения срока обычной годовой ренты при однократном начислении процентов в году.



Ответ А.

10. Укажите формулу линейной интерполяции.



Ответ Б.

11. Аннуитет — это

а) единовременный вклад в банк

б) вложение в ценные бумаги

в) серия равновеликих платежей в течение определенного количества периодов

Ответ В.

12. Финансовая рента или аннуитет это:

а) поток платежей, разных по величине через разные промежутки времени;

б) поток платежей, одинаковых по величине через разные промежутки времени;

в) поток платежей, одинаковых по величине через равные промежутки времени.

Ответ В.

13. Наращение суммы финансовой ренты это:

а) сумма всех последовательных платежей;

б) сумма всех последовательных платежей с начисленными на них процентами на любой момент времени;

в) сумма начисленных процентов на определенные платежи;

г) сумма всех последовательных платежей с начисленными на них процентами к концу их срока.

Ответ Г.

14. Современная величина потока платежей это:

а) сумма его членов дисконтированных на некоторый момент времени;

б) сумма его членов дисконтированных на начало потока платежей.

в) сумма его членов дисконтированных на середину потока платежей.

Ответ Б.

15. По продолжительности периода ренты бывают:

а) годовые – с выплатой 1 раз в году;

б) р – срочные, с выплатой несколько раз в году;

в) с периодом выплат, превышающими год;

г) с периодом выплат через бесконечно малые промежутки времени.

Ответ А,Б, В.

16. По числу начислений процентов различают ренты:

а) с начислением процентов один раз в году;

б) несколько раз в году;

в) произвольно, в зависимости от требований кредитора;

г) непрерывно.

Ответ А,Б, Г.

17. По моменту выплаты платежей различают:

а) постнумерандо (в конце периода);

б) в зависимости от финансового состояния, участвующих сторон;

в) в середине каждого периода;

г) пренумерандо (в начале периода).

Ответ А, В, Г.

18. Как определяются обобщающие характеристики финансовых рент пренумерандо:

а) в результате математической обработки данного вид потока платежей;

б) методом прямого счета;

в) по формулам аннуитетов постнумерандо, увеличенных на один множитель наращения или дисконтирования.

Ответ В.

19. Два аннуитета считаются эквивалентными, если:

а) равны их наращенные суммы;

б) равны их современные величины, приведенные к любому моменту времени;

в) равны их современные величины, приведенные к одному и тому же моменту времени.

Ответ В.

20. При отсрочке выплаты задолженности:

а) уменьшена величина платежа и срока выплат;

б) увеличен срок аннуитета и размер платежа;

в) увеличена величина платежа;

г) должен увеличиваться срок аннуитета.

Ответ В.