Тема Рыночные структуры и стратегия поведения Тема Рынки факторов производства
 Скачать 1.04 Mb. Скачать 1.04 Mb.
|
 Проверяемое задание 2 Проверяемое задание 2Тема 7. Рыночные структуры и стратегия поведения Тема 8. Рынки факторов производства Задача 1. На рынке функция предложения некоторой совершенно конкурентной фирмы задана уравнением 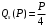 . Значение постоянных издержек фирмы составляет . Значение постоянных издержек фирмы составляет 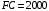 ден.ед. Известно, что в некий период времени рыночная цена установилась на уровне ден.ед. Известно, что в некий период времени рыночная цена установилась на уровне 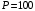 ден.ед. Определить величину максимальной прибыли фирмы при заданной цене. Построить график предложения фирмы. ден.ед. Определить величину максимальной прибыли фирмы при заданной цене. Построить график предложения фирмы.Решение: Оптимальный объем, при котором фирма максимизирует прибыль, определяется из условия: 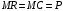 Величина прибыли при 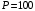 ден.ед. равна ден.ед. равна 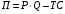 , ,предложение фирмы 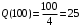 ден.ед, ден.ед,  выручка выручка 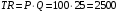 ден.ед., ден.ед., 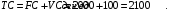  величина максимальной прибыли фирмы при заданной цене величина максимальной прибыли фирмы при заданной цене 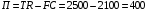 ден.ед. ден.ед.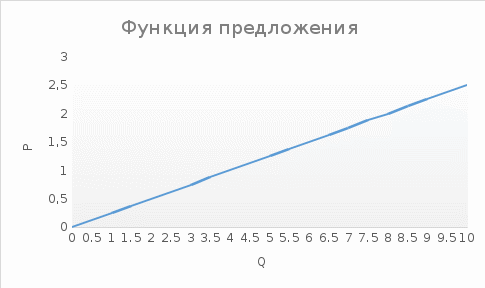 Рисунок 1. График предложения фирмы. Задача 2. Фирма действует в условиях несовершенной конкуренции. Функция предельной выручки (дохода) задана условием 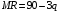 . При этом зависимость общих издержек от объема выпуска принимает вид . При этом зависимость общих издержек от объема выпуска принимает вид 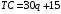 . Определить, какой степенью власти на рынке обладает фирма (индекс Лернера). . Определить, какой степенью власти на рынке обладает фирма (индекс Лернера).Решение: Индекса Лернера (степень власти фирмы на рынке) определим по формуле: 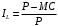 (1) (1)для этого найдем устанавливаемую монополистом цену и соответствующую ей величину предельных затрат 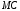 . Максимальная прибыль фирмы в условиях несовершенной конкуренции . Максимальная прибыль фирмы в условиях несовершенной конкуренции 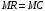 , где , где 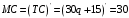  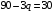  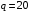 Для линейной кривой предельного дохода вида 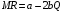 функция спроса принемает вид функция спроса принемает вид 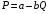  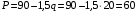 . .По формуле (1): 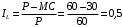 . .Индекс Лернера 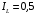 , что свидетельствует о фирма находится в серединном положении между монополистом и совершенной конкуренции. , что свидетельствует о фирма находится в серединном положении между монополистом и совершенной конкуренции.Задача 3. Производственная функция фирмы имеет вид: 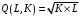 . Ставка зарплаты равна значению . Ставка зарплаты равна значению 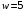 ден.ед., а ставка арендной платы за капитал ден.ед., а ставка арендной платы за капитал 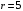 ден.ед. Уровень выпуска равен 20 ед. Какой будет оптимальная комбинация ресурсов ден.ед. Уровень выпуска равен 20 ед. Какой будет оптимальная комбинация ресурсов 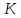 и и 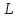 ? ?Решение: Для определения оптимальной комбинации факторов производства необходимо рассчитать равновесие фирмы: при оптимальной комбинации ресурсов будет выполняться равенство: 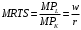 (2) (2) при объеме производства при объеме производства 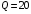 выполняется равенство выполняется равенство 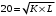  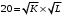 или или 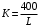  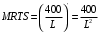 . .По формуле (2): 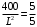  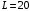 , , 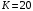 . .Ответ: оптимальная комбинация ресурсов 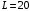 , , 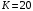 . .Задача 4. Фирма-монополист продает свою продукцию на двух сегментах рынка с различной эластичностью спроса 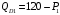 и и 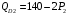 . Функция общих затрат принимает вид . Функция общих затрат принимает вид 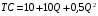 . Общий объем спроса на продукцию фирмы-монополиста . Общий объем спроса на продукцию фирмы-монополиста 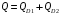 . .Рассчитать: – значения цен на каждом из сегментов, при которых фирма-монополист получит максимум прибыли; – объем продаж на каждом из сегментов и прибыль фирмы-монополиста при запрещении ценовой дискриминации. Решение: Максимальную прибыль фирма – монополист получит при соблюдении равенства: 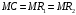 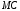 - есть производная функции - есть производная функции 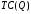 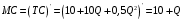 . Из условия . Из условия 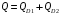 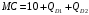 . .Для линейной кривой предельного дохода вида 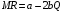 функция спроса принемает вид функция спроса принемает вид 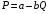 Выразим функции спроса в виде обратных: 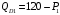  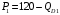 ; ;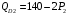  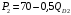 Соответствующие функции 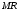 будут выглядеть как : будут выглядеть как :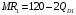 ; ;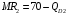 . .Так как равенство 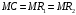 соблюдается во всех сегментах можно составить систему уровнений: соблюдается во всех сегментах можно составить систему уровнений: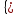 ; ;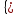 ; ;Решая систему: 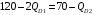  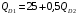  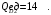 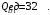 Расчитаем оптимальные цены при таком количестве объема: 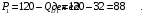 ; ;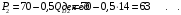 При запрещении ценовой дискриминации продажи в обоих сигментах рынка будет осуществлятся по единой цене. Оптимальный объем производства определяется равенством 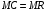 . .Функции суммарного спроса и предложения примут вид: 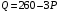 ; ;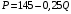 . .Усредненный доход в обоих сегментах: 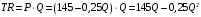 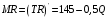 Из условия 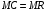 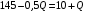 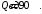 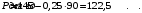 Общая прибыль фирмы при запрещении дискриминации: 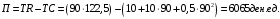 Ответ: максимум прибыли фирма получит при ценах 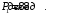 , , 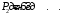 При запрещении ценовой дискриминации объем продаж 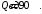 , прибыль фирмы , прибыль фирмы 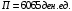 |
