Лекция 5. Тема Теория сравнений 15. Сравнения в кольце целых чисел и их свойства 15 Сравнения по фиксированному модулю
 Скачать 28.13 Kb. Скачать 28.13 Kb.
|
|
Тема 2. Теория сравнений § 15. Сравнения в кольце целых чисел и их свойства 15.1. Сравнения по фиксированному модулю Опр.1 Целые числа а и b сравнимы между собой по модулю (натуральному числу) m (m > 1) и пишут 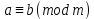 , если при делении этих чисел на m получают одинаковые остатки. , если при делении этих чисел на m получают одинаковые остатки.Пример. 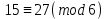 , т.к. 15 = 6 , т.к. 15 = 6 2 + 3; 27 = 6 2 + 3; 27 = 6 4 + 3. 4 + 3.Теорема1. Если целые числа а и b сравнимы по модулю m, то (а – b)  m. m.Доказательство: т.к. 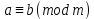 , то по опр.1 а = mq1 + r, b = mq2 + r. , то по опр.1 а = mq1 + r, b = mq2 + r.а – b = m(q1 – q2)  (a – b) (a – b) m. m.Опр.2 Целые числа а и b сравнимы по модулю m (m > 1), если (а – b)  m. m.Теорема2. Отношение сравнимости на множестве целых чисел Z является отношением эквивалентности. Доказательство: покажем, что отношение сравнимости по данному модулю m обладает рефлексивностью, т.е.  . .а – а = 0, а 0 делится на любое число, значит 0  m, т.е. m, т.е. 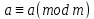 . .Покажем, что отношение сравнимости по данному модулю m обладает симметричностью, т.е.   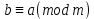 . Это очевидно. . Это очевидно.Покажем, что отношение сравнимости по данному модулю m обладает транзитивностью, т.е. 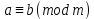    . .а – с = ((а – b) + (b – c))  m, (а- b) m, (а- b)  m, и (b – c) m, и (b – c) m, значит и (а – с) m, значит и (а – с)  m, т.е. m, т.е. 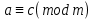 . Теорема доказана. . Теорема доказана.Свойства 10. Обе части сравнения можно умножать на любое целое число n. Доказательство: покажем, что 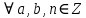  . .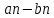 = n(a – b) = n(a – b) m т.к. (а- b) m т.к. (а- b)  m. m.20. К обеим частям сравнения можно прибавлять любое целое число. Доказательство: покажем, что 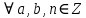 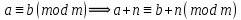 . .(а + n) – (b + n) = (a + b)  m. По опр.2 m. По опр.2  . .30. Сравнения по одному модулю можно складывать и вычитать. Доказательство: покажем, что 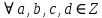 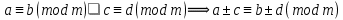 . .(а ± c) – (b ± d) = (a - b) 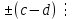 m, т.к. (а- b) m, т.к. (а- b)  m m 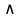 (с – d) (с – d)  . .40. Сравнения по одному модулю можно перемножать. Доказательство: покажем, что 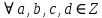  . .(а c) – (bd) = (aс - bс)  m, т.к. m, т.к. (а- b)  m m 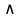 (с – d) (с – d)  . .50. Из одной части сравнения слагаемые можно переносить в другую часть с противоположным знаком. Доказательство: покажем, что   . .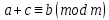 , ,  - рефлексивность. По свойству 30 - рефлексивность. По свойству 30 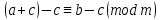 или а или а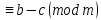 . .60. К любой части сравнения можно прибавить произвольное целое число, кратное модулю, т.е. 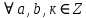  . .Доказательство:  = ((a – b) + km) = ((a – b) + km) mт.к. (а- b) mт.к. (а- b)  m m 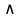 km km  m. m.70. Сравнения можно возводить в любую натуральную степень:  , ,  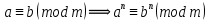 . .Доказательство: методом математической индукции. 1. n = 1 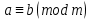 - по условию. - по условию.2. n = k. Пусть верно 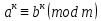 . .3. Покажем, что формула верна для n = k + 1. Имеем 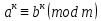 ; ; 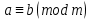 . По свойству 4 эти сравнения можно перемножить, получим . По свойству 4 эти сравнения можно перемножить, получим 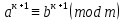 - что и требовалось доказать. - что и требовалось доказать.80. Обе части сравнения можно делить на их общий делитель d, взаимно простой с m. Доказательство: покажем, что  , таких, что а , таких, что а d и b d и b  d, и (m, d) = 1, из условия d, и (m, d) = 1, из условия 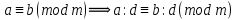 . .Т.к. а  d и b d и b  d, то а = а1d и b = b1d. Разность а – b = а1d - b1d = (а1 - b1 )d. Т.к. (а1 - b1)d d, то а = а1d и b = b1d. Разность а – b = а1d - b1d = (а1 - b1 )d. Т.к. (а1 - b1)d и (d, m) = 1, то (а1 - b1) и (d, m) = 1, то (а1 - b1) , значит а1 , значит а1 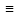 b1 (modm). b1 (modm). a1 = 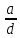 , b1 = , b1 = 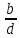 и значит и значит  . .90. Если в выражении f(a1, a2, …,ak) =  … … , где А,a1, a2, …,ak , где А,a1, a2, …,ak  Z; m1, m2, …,mk–неотрицательные целые числа, заменить А,a1, a2, …,ak на сравнимые с ними по модулю m соответствующие числа B,b1, b2, …,bk, то g(b1, b2, …,bk) сравнимо с f(a1, a2, …,ak) по модулю m. Z; m1, m2, …,mk–неотрицательные целые числа, заменить А,a1, a2, …,ak на сравнимые с ними по модулю m соответствующие числа B,b1, b2, …,bk, то g(b1, b2, …,bk) сравнимо с f(a1, a2, …,ak) по модулю m.Доказательство: по условию  , ,  , …, , …,  . Эти сравнения соответственно возведем в степени m1, m2, …,mk. Получим . Эти сравнения соответственно возведем в степени m1, m2, …,mk. Получим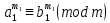 , , 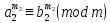 , …, , …, 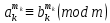 . .По условию 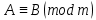 , перемножая эти сравнения, получим , перемножая эти сравнения, получим . Суммируя сравнения такого вида, получим . Суммируя сравнения такого вида, получим 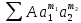 … …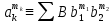 … …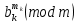 . . И f(a1, a2, …,ak) 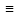 g(b1, b2, …,bk) g(b1, b2, …,bk)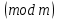 . .Следствие. Если в многочлене с целыми коэффициентами f(x) = anxn + an-1xn-1 + …+a1x + a0, определенном на множестве целых чисел Z, заменить коэффициенты an, an-1, …a1, a0 коэффициентами bn, bn-1, …b1, b0, сравнимыми по модулю m соответственно, то многочлен g(x) = bnxn + bn-1xn-1 + …+b1x + b0сравним с данным многочленом f(x) при любом целом х. Доказательство: пусть  и запишем очевидное: и запишем очевидное: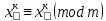 , х , х 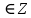 . . 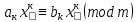 , к = , к =  . Суммируя эти сравнения по к от n до 0: . Суммируя эти сравнения по к от n до 0: 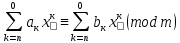 или f(х) или f(х)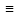 g(х) g(х)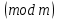 . .15.2. Свойства сравнений 10. Все части сравнения 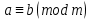 можно умножать на любое натуральное число. можно умножать на любое натуральное число.Доказательство: (а – b)  m (по условию). Значит а – b = кm. Это равенство умножим на натуральное число n: аn – bn = (кm)n m (по условию). Значит а – b = кm. Это равенство умножим на натуральное число n: аn – bn = (кm)n  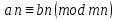 . .20. Обе части сравнения 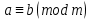 и модуль можно разделить на их общий делительd. и модуль можно разделить на их общий делительd.Доказательство: пусть а  , b , b , m , m  , тогда а = da1, b = db1, m = dm1. Из условия следует, что а – b = mt. Подставляя, получим: da1 - db1 = (dm1)t - d(m1t), тогда a1 - b1 = m1t или , тогда а = da1, b = db1, m = dm1. Из условия следует, что а – b = mt. Подставляя, получим: da1 - db1 = (dm1)t - d(m1t), тогда a1 - b1 = m1t или 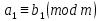 . .  , ,  , ,  , и значит , и значит 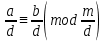 . .30. Если  по некоторым модулям m1, m2, …, mk, то по некоторым модулям m1, m2, …, mk, то  по их наименьшему общему кратному: по их наименьшему общему кратному:  (mod [m1, m2, …, mk]). (mod [m1, m2, …, mk]).Доказательство: т.к. :  (modm1), (modm1),  (modm2),…, (modm2),…,  (modmк), то (а - b) делится на m1, m2, …, mk, следовательно (а – b) для модулей m1, m2, …, mk является общим кратным. Поэтому (а – b) (modmк), то (а - b) делится на m1, m2, …, mk, следовательно (а – b) для модулей m1, m2, …, mk является общим кратным. Поэтому (а – b) [m1, m2, …, mk], следовательно [m1, m2, …, mk], следовательно  (mod [m1, m2, …, mk]). (mod [m1, m2, …, mk]).40. Если  (modm) (modm) 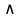 m m d, то d, то  (modd). (modd).Доказательство: (а – b)  m, m m, m d следовательно (а – b) d следовательно (а – b) d (транзитивность), значит d (транзитивность), значит  (modd). (modd).50. Если одна часть сравнения  (modm) и модуль делятся на число d, то и вторая часть сравнения делится на это число d. (modm) и модуль делятся на число d, то и вторая часть сравнения делится на это число d.Доказательство: пусть а  d и m d и m d. Докажем, что и b d. Докажем, что и b d. d.(а – b)  m m  а – b = mt, b = a – mt. а – b = mt, b = a – mt.Т.к. а  d и m d и m d, то (а – mt) d, то (а – mt) d d b b d. d.60. Если  (modm), то (а, m) = (b, m). (modm), то (а, m) = (b, m).Доказательство: обозначим Da,m – множество общих делителей чисел а и m, Db,m – множество общих делителей чисел b и m. Пусть 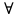 d d 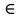 Da,m –произвольный делитель чисел а и m. Тогда из условия Da,m –произвольный делитель чисел а и m. Тогда из условия  (modm) найдем, что b = а – mt (modm) найдем, что b = а – mt  b b d d  d d 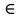 Db,m Db,m  Da,m Da,m Db,m (1). Db,m (1).С другой стороны, пусть 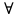 к к 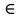 Db,m –произвольный делитель чисел b и m и является делителем чисел а и m ,т.к. а = b + mt Db,m –произвольный делитель чисел b и m и является делителем чисел а и m ,т.к. а = b + mt  Db,m Db,m  Dа,m (2). Dа,m (2).Из (1) и (2) следует, что Db,m 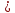 Dа,m , значит (а, m) = (b, m). Dа,m , значит (а, m) = (b, m).§ 16. Вывод признаков делимости Одним из методов нахождения делителя, основанных на сравнении, является метод Паскаля. Пусть некоторое натуральное число а, записанное в системе счисления с основанием q, имеет вид: а = аnqn + an-1qn-1 + …+ a1q + a0, где 0 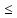 аn,an-1, … a1, a0 < q, аn ≥ 1. И пусть число b = аnrn + an-1rn-1 + …+ a1r + a0. Тогда из условия аn,an-1, … a1, a0 < q, аn ≥ 1. И пусть число b = аnrn + an-1rn-1 + …+ a1r + a0. Тогда из условия  (modm) следует, что если b (modm) следует, что если b  m , то и a m , то и a  m. Если b не делится на m, то и а не делится на m. Это и есть признак Паскаля. m. Если b не делится на m, то и а не делится на m. Это и есть признак Паскаля.Пример. Рассмотрим числа 3, 9. Запись в десятичной системе счисления: а = аn10n + an-110n-1 + …+ a110 + a0. При делении 10к на 3 и на 9 в остатке получается 1, т.е. r0 = r1 = …= rn = 1 и тогда b = аn1 + an-11+ …+ a11 + a0 = аn + an-1+ …+ a1 + a0 . Вывод: натуральное число а делится на 3 (на 9) тогда и только тогда, когда на 3 (на 9) делится сумма цифр этого числа, записанного в десятичной системе счисления. Выведем признак делимости на 11. Заметим, что четная степень 102к при делении на 11 в остатке дает 1, а при делении нечетной степени числа 102к – 1 на 11 в остатке дает -1. Тогда b = a0 + a1(-1) + а2 + а3 (-1)+ а4 + … = (a0 + а2 + а4 + …) – (a1 + а3 + а5 + …). Итак, натуральное число делится на 11 тогда и только тогда, когда разность между суммой цифр, стоящих на четных местах и суммой цифр, стоящих на нечетных местах, делится на 11. Пример. Делится ли на 11 число 53746? Решение: 6 + 7 + 5 – (3 + 4) = 18 – 7 = 11 – делится на 11, значит и 53746 тоже делится на 11. |
