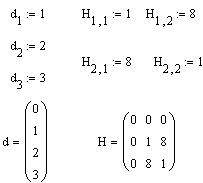|
|
Лекция 2_Работа с векторами и матрицами. Тема Вектора и матрицы
Важным типом данных в системе MathCAD являются массивы. Массив- имеющая уникальное имя совокупность конечного числа числовых или символьных элементов, упорядоченных заданным образом и имеющих определенные адреса. В системе MathCAD используются массивы двух типов: одномерные (векторы) и двумерные (матрицы).
Для ввода векторов и матриц можно использовать кнопку  панели наборных математических элементов Matrix, которая ,в свою очередь, включается нажатием соответствующей кнопки на панели Math. Но горазжо проще использовать сочетание клавишь [Ctrl+M]. Оба выше указанных действия приводят к появлению диалогового окна Insert Matrix, в котором необходимо указать число строк и столбцов для вводимой матрицы (вектора).
|
 
|
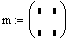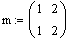
В результате в документе появляется шаблон матрицы, который можно заполнить требуемыми данными. Переход от символа к символу внутри шаблона совершается с помощью клавиши Tab(Табуляция).
|
Массив можно определить и вручную, поэлементно.
|
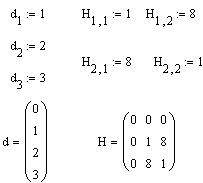
Для указания нижнего индекса используется клавиша [ (квадратная скобка). Если индекс двойной (у матрицы), то индексы вводятся через запятую.
|
Заполнение массивов может быть организовано с помощью ранжированных переменных и функций пользователя.
Тема 2. Векторные матричные операторы
Для работы с векторами и матрицами система Math CAD содержит ряд операторов и функций. Введём следующие обозначения: для векторов – V, для матриц – M, и для скалярных величин – Z.
Оператор
|
Ввод
|
Назначение оператора;
|
V1+V2
|
V1+V2
|
Сложение двух векторов V1 и V2;
|
V1-V2
|
V1-V2
|
Вычитание двух векторов V1и V2;
|
-V
|
-V
|
Смена знака у элементов вектора V;
|
-M
|
-M
|
Смена знака у элементов матрицы M;
|
V-Z
|
V-Z
|
Вычитание из вектора V скаляра Z;
|
Z*V, V*Z
|
Z*V, V*Z
|
Умножение вектора V на скаляр Z;
|
Z*M, М*Z
|
Z*M, М*Z
|
Умножение матрицы M на вектор V;
|
V1*V2
|
V1*V2
|
Умножение двух векторов V1 и V2;
|
M*V
|
M*V
|
Умножение матрицы M на вектор V;
|
M1*M2
|
M1*M2
|
Умножение двух матриц M1 и M2;
|
V/Z
|
V/Z
|
Деление вектора V на скаляр Z;
|
M/Z
|
M/Z
|
Деление матрицы M на скаляр Z;
|
M-1
|
M^-1
|
Обращение матрицы M;
|
Mn
|
M^n
|
Возведение матрицы M в степень n;
|
| V |
|
Ѕ V
|
Вычисление квадратного корня из μV;
|
| M|
|
Ѕ M
|
Вычисление определителя матрицы M;
|
VT
|
V Ctrl !
|
Транспонирование вектора V;
|
MT
|
M Ctrl !
|
Транспонирование матрицы M;
|
V1xV2
|
V1 Ctrl* V2
|
Кросс – умножение двух векторов V1 и V2;
|
V
|
V ”
|
Получение комплексно – сопряженного вектора;
|
M
|
M ”
|
Получение комплексно – сопряженной матрицы;
|
?V
|
Alt $ V
|
Вычисление суммы элементов вектора V;
|
V
|
V Ctrl –
|
Векторизация вектора V;
|
M
|
M Ctrl –
|
Векторизация матрицы M;
|
M
|
M Ctrl ^n
|
Выделение n–го столбца матрицы M;
|
Vn
|
V [ n
|
Выделение n–го элемента вектора V;
|
Mm,n
|
M [(m,n)
|
Выделение элемента (m, n) матрицы M.
|
Под понятием “векторизация” подразумевается одновременное проведение математических операций в их скалярном значении над всеми элементами вектора или матрицы, помеченными векторизации. Это можно понимать и как возможность параллельных вычислений.
Если А и В – векторы, то А*В даёт скалярное произведение этих векторов. Но то же произведение под знаком векторизации создает новый вектор, каждый j-й элемент которого есть произведение j –х элементов векторов А и В. Векторизация позволяет использовать скалярные операторы и функции с массивами.
Тема 3. Векторные и матричные функции
Существует также ряд встроенных векторных и матричных функций. Приведем векторные функции, входящие в систему Math CAD:
lenght (V)
|
возвращает длину вектора;
|
last (V)
|
возвращает индекс последнего элемента;
|
max (V)
|
возвращает максимальный по значению элемент;
|
min (V)
|
возвращает минимальный по значению элемент;
|
Re (V)
|
возвращает вектор действительных частей вектора с комплексными элементами;
|
Im (V)
|
возвращает вектор мнимых частей вектора с комплексными элементами;
|
ε (i, j, k)
|
полностью асимметричный тензор размерности три. i, j, k должны быть целыми числами от 0 до 2 (или между >ORIGIN и ORIGIN+2, если ORIGIN≠0). Результат равен 0, если любые два аргумента равны, 1 – если три аргумента являются чётной перестановкой (0, 1, 2), и минус 1, если три аргумента являются перестановкой (0, 1, 2), кратной 2 и некратной 4.
|
Для работы с матрицами также существует ряд встроенных функций. Они перечислены ниже:
Augment (M1, M2)
|
Объединяет в одну матрицы М1 и М2, имеющие одинаковое число строк (объединение идёт “бок о бок”);
|
identity (n)
|
Создаёт единичную квадратную матрицу размером n*n;
|
stack (M1, M2)
|
Объединяет в одну матрицы М1 и М2, имеющие одинаковое число столбцов, располагая М1 над М2;
|
submatrix(A,ir,jr,ic,jc)
|
возвращает субматрицу, состоящую из всех элементов, содержащихся в строках от ir по jr и столбцов с ic по jc (irJjrи icJjc);
|
diag (V)
|
Создаёт диагональную матрицу, элемент главной диагонали которой – вектор V;
|
matrix (m,n,f)
|
Матрицу, в которой (i,j)-й элемент содержит f(i,j), где i= 0, 1, …m и j=0, 1, …n;
|
Re (M)
|
Возвращает матрицу действительных частей матрицы М с комплексными элементами;
|
Im (M)
|
Возвращает матрицу мнимых частей матрицы М с комплексными элементами.
|
Специальные характеристики матриц возвращаются следующими функциями:
cols (M)
|
возвращает число столбцов матрицы М;
|
rows (M)
|
возвращает число строк матрицы М;
|
rank (M)
|
возвращает ранг матрицы М;
|
tr (M)
|
возвращает след (сумму диагональных элементов) квадратной матрицы М;
|
mean (M)
|
возвращает среднее значение элементов массива М;
|
median (M)
|
возвращает медиану элементов массива М;
|
cond1 (M)
|
возвращает число обусловленности матрицы, вычисленное в норме L1;
|
cond2 (M)
|
возвращает число обусловленности матрицы, вычисленное в норме L2;
|
conde (M)
|
Возвращает число обусловленности матрицы, вычисленное в норме евклидова пространства;
|
condi (M)
|
Возвращает число обусловленности матрицы, основанное на равномерной норме;
|
norm1 (M)
|
Возвращает L1, норму матрицы М;
|
norm2 (M)
|
Возвращает L2, норму матрицы М;
|
norme (M)
|
Возвращает евклидову норму матрицы М;
|
normi (M)
|
Возвращает неопределённую норму матрицы М.
| |
|
|
Скачать 95 Kb.