Лабораторная работа. Лабораторная работа №1. Вектора

• Название: Вектора
• Анкор: Лабораторная работа
• Дата: 09.12.2020
• Размер: 330.41 Kb.
• Имя файла: Лабораторная работа №1.docx
• Тип: Документы; #158674

Функции Mathcad, используемые в работе

1. 
   rows(A) - функция для определения количества элементов в одномерном массиве данных (векторе), А – название вектора
   
2. 
   augment(A, B, C, …) – функция объединения векторов и матриц в одну матрицу по ширине (у объединяемых массивов должно быть одинаковое количество строк), A, B, C, … - названия векторов и матриц
   
3. 
   submatrix(A, x1, x2, y1, y2) – А – название матрицы (вектора); х1, х2 – номера начальной и конечной строк, выделяемой части матрицы (вектора); у1, у2 – номера начального и конечного столбцов, выделяемой части матрицы (вектора)
   
4. 
   mean(A) - определение среднего значения одномерного набора данных – вектора или одного из столбцов матрицы, А – название вектора
   
5. 
   var(A) – функция определения дисперсии без компенсации смещения одномерного массива данных
   
6. 
   Var(А) - функция определения дисперсии с компенсацией смещения одномерного массива данных
   
7. 
   stdev(A) – функция определения среднего квадратического отклонения без компенсации смещения для одномерного массива данных
   
8. 
   Stdev(A) – функция определения среднего квадратического отклонения c компенсацией смещения для одномерного массива данных
   
9. 
   skew(A) – функция определения коэффициента ассиметрии
   
10. 
    dnorm (x, xcp, xcko) – плотность вероятности нормального распределения
    
11. 
    pnorm (x, xcp, xcko) – функция вероятности нормального распределения
    
12. 
    qnorm (x, xcp, xcko) – обратная функция вероятности нормального распределения
    

x – значение случайной величины, хср – среднее значение, xcko – среднее квадратическое отклонение

13. 
    dlnorm (x, xcp, xcko) – плотность вероятности логарифмически нормального распределения
    
14. 
    plnorm (x, xcp, xcko) – функция вероятности логарифмически нормального распределения
    
15. 
    qlnorm (x, xlcp, xlcko) – обратная функция вероятности логарифмически нормального распределения
    

x – значение случайной величины, хlср – среднее значение логарифмов случайной величины, xlcko – среднее квадратическое отклонение логарифмов случайной величины

16. 
    dchisq (x, k) – плотность вероятности распределения Пирсона (χ²)
    
17. 
    pnorm (x, k) – функция вероятности распределения Пирсона (χ²)
    
18. 
    qnorm (x, k) – обратная функция вероятности распределения Пирсона (χ²)
    

x – значение случайной величины, k – число степеней свободы.

Основными командами Mathcad для расчетов числовых статистических характеристик рядов случайных данных являются следующие функции:

• 
   mean(x) — выборочное среднее значение;
  
• 
   median (х) — выборочная медиана (median) — значение аргумента, которое делит гистограмму плотности вероятностей на две равные части;
  
• 
   var (х) — выборочная дисперсия (variance);
  
• 
   stdev(x) — среднеквадратичное (или стандартное) отклонение (standard deviation);
  
• 
   max(x) ,min(x) — максимальное и минимальное значения выборки;
  
• 
   mode(x) — наиболее часто встречающееся значение выборки;
  

Регрессия

19. 
    line(vx,vy) –регрессия линейной функцией у(x)=a·x+b
    

vx и vy – массивы, содержащие значения координат экспериментальных точек.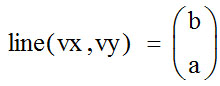

20. 
    regress(vx,vy,n) – регрессия полиномиальной n-степени функцией
    

vx и vy – массивы, содержащие значения координат экспериментальных точек,

n – степень полиномиальной функции.

21. 
    regress(vx,vy,2)–регрессия полиномиальной функцией 2-степени
    

у(x)=a·x²+b·x+c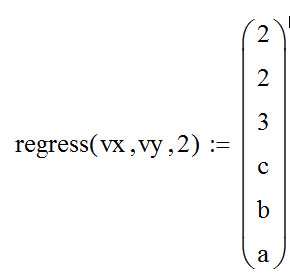

22. 
    regress(vx,vy,3) – регрессия полиномиальной функцией 3-степени у(x)=a·x³+b·x²+c·x+d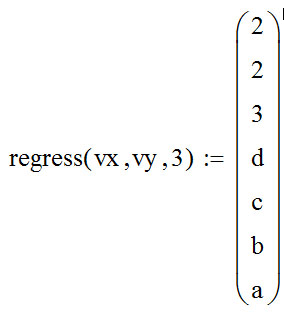
    

23. 
    expfit(vx,vy,vg) – регрессия экспоненциальной функцией у(x)=a·е^b·x+c
    

vx и vy – массивы, содержащие значения координат экспериментальных точек, vg – это вспомогательный трехкомпонентный вектор, содержащий приблизительные значения параметров a,b,c
у(x)=a·е^b·x+c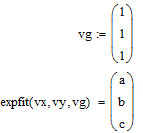

24. 
    pwrfit(vx,vy,vg) – регрессия степенной функцией у(x)=a·x^b+c
    

vx и vy – массивы, содержащие значения координат экспериментальных точек, vg – это вспомогательный трехкомпонентный вектор, содержащий приблизительные значения параметров a,b,c

у(x)=a·x^b+c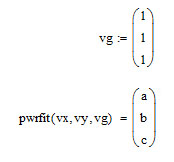



Оценка точности аппроксимирующей функции

1. 
   Для оценки качества каждой из построенных регрессионных зависимостей рассчитывается сумма квадратов отклонений заданных данных от найденных регрессий. Выбрать наилучшее уравнение регрессии (используя метод наименьших квадратов).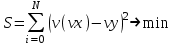
   

В этой формуле vy - значения массива эксперементальных значений и y(vx) массив значений регрессионной функции в точках заданных массивом эксперементальных данных vx.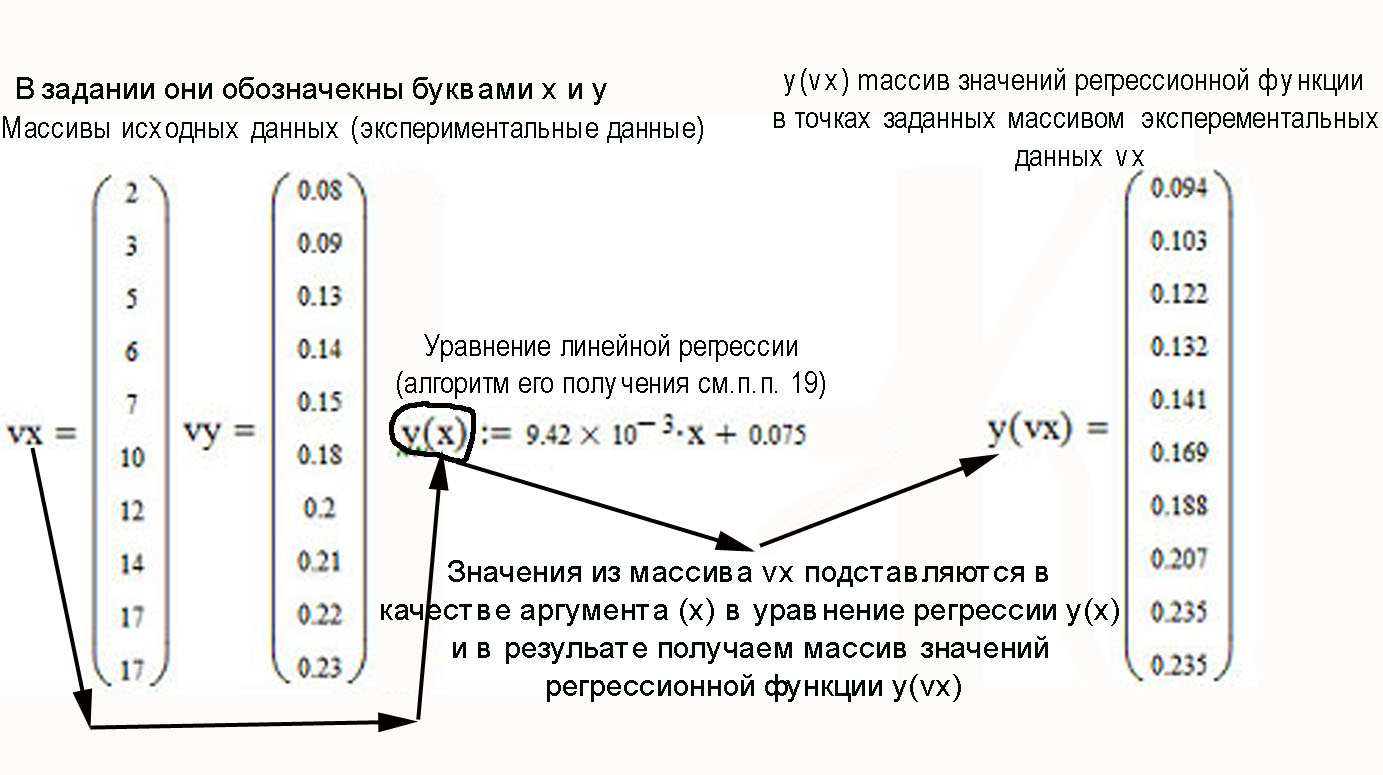

2. 
   Корреляция – это взаимосвязь двух или нескольких случайных параметров. Когда одна величина растет или уменьшается, другая тоже изменяется.
   

Коэффициент корреляции определяет степень взаимозависимости одной переменной от другой. Чем он ближе по значению к 1 или -1 – тем сильнее взаимосвязаны массивы экспериментальных переменных vx и vy.

Математически формула выглядит так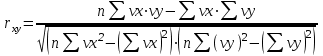


В Mathcad коэффициент корреляции рассчитывается при помощи встроенной команды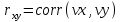



vx и vy – массивы, содержащие значения координат экспериментальных точек.
Для оценки точности полученных регрессионных зависимостей так же можно используем коэффициент корреляции.

Для выбора наилучшей регрессионной функции производят расчет коэффициента корреляции между рядом значений массивом эксперментальных значений функции и массивом значений полученным в результате расчета регрессионной функцией при использовании качестве аргумента массива аргументов экспериментальных данных

В этом случае исследуется кореляционная зависимость между массивом эксперементальных значений функции (vy) и массивом значений регрессионной функции y(vx) в точках заданных массивом эксперементальных данных vx.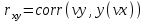



Чем ближе данный коэффициент к единице, тем лучше выбранная функция аппроксимирует экспериментальные данные.

Пример:

Сравниваются 2 регрессионных уравнения y(vx) и y1(vx)

corr(vy,y(vx))=0.945 corr(vy,y1(vx))=0.991

Коэффициент корреляции функции y1(vx) больше (0.991) и соответственно данная функции наиболее точно описывает экспериментальные данные.

3. 
   Метод наименьших квадратов заключается в вычислении среднеквадратического отклонения значения случайной величины от значений регрессионной функции и нахождения таких параметров , при которых это отклонение будет минимальным.
   

Для вычисления среднеквадратического отклонения в Mathcad существует встроенная функция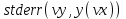


В этой формуле vy – уже знакомый нам массив эксприментальных значений, y(vx) массив значений регрессионной функции y(vx) в точках заданных массивом эксперементальных данных vx.

4. 
   После определения регрессионных зависимостей в Mathcad, актуальным является выбор из их совокупности наилучшей функции, с точки зрения адекватности описания исходных экспериментальных данных. В качестве критерия, позволяющего выбрать наилучшую регрессионную модель, предлагается использовать коэффициент детерминации. численно равный коэффициенту корреляции в квадрате. Значение коэффициента корреляции в Mathcad позволяет рассчитать функция corr(vx, vy), где vx и vy – два вектора значений.
   

Математически коэффициент детерминации описывается формулой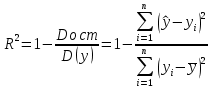



Dост, D(y) – дисперсия остаточная (необъясненная) и общая дисперсия результативного признака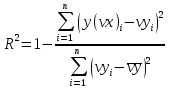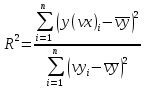




Где vy – наблюдаемое значение зависимой переменной; y(vx) – значение зависимой переменной полученной по уравнению регресси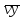и; - среднеее значение наблюдаемой (эксперементальной переменной).
Коэффициент детерминации R² численно равный коэффициенту корреляции r в квадрате. Значение коэффициента корреляции в Mathcad позволяет рассчитать функция corr(A,B), где A и B – два вектора значений.
R²=r²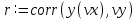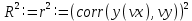