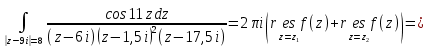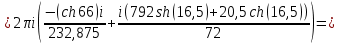Задание 3(21). Тема Вычисление интегралов с помощью вычетов Задание
 Скачать 1.49 Mb.
|
|
| Вариант 0 |  |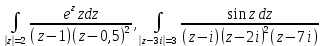
| Вариант 1 |  |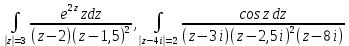
| Вариант 2 |  |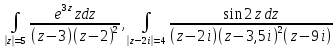
| Вариант 3 |  |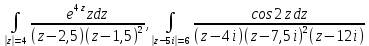
| Вариант 4 |  |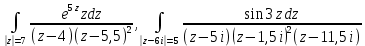
| Вариант 5 |  |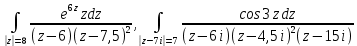
| Вариант 6 |  |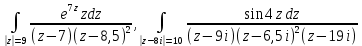
| Вариант 7 |  |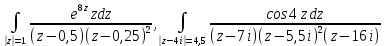
| Вариант 8 |  |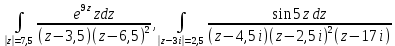
| Вариант 9 |  |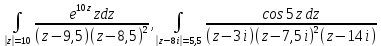
Рекомендации по выполнению задания
Для каждого из заданных интегралов выполнить следующие действия:
Выяснить, какие особые точки подынтегральной функции находятся внутри контура интегрирования. Определить тип каждой из этих точек.
Найти вычеты функции в указанных точках.
Вычислить интеграл, используя основную теорему о вычетах.
Образец выполнения задания
С помощью основной теоремы о вычетах вычислить интегралы
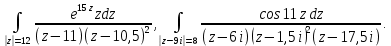
Решение.
Рассмотрим интеграл
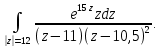
Конечными особыми точками функции
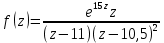являются точк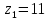и 
и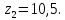 
Обе они находятся внутри контура 
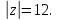В точке 
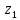функция 
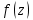имеет простой полюс, а в точке 
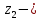полюс второго порядка. В соответствии с формулами для вычисления вычета функции в случае полюса имеем: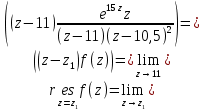
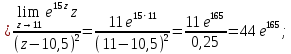
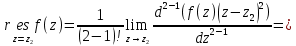
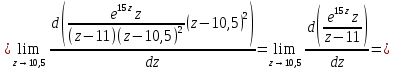
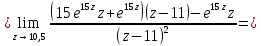
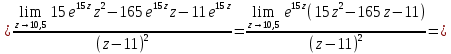
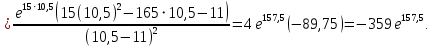
Используя основную теорему о вычетах, получаем:
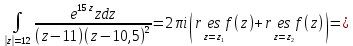
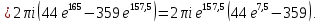
Рассмотрим интеграл
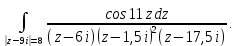
Конечными особыми точками функции
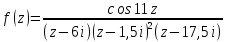являются точк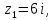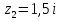и 
и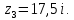 
Внутри контура 
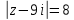находятся только точк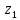и и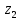 
. В первой из них функция 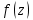имеет простой полюс, а во второй – полюс второго порядка. В соответствии с формулами для вычисления вычета функции в случае полюса имеем: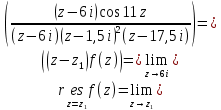 
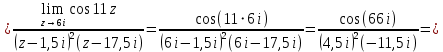
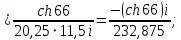
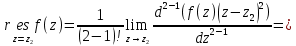
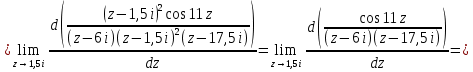
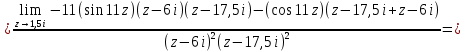
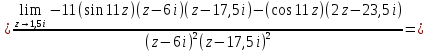
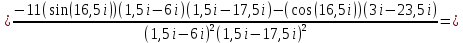
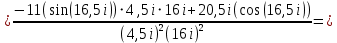
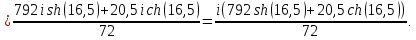
Используя основную теорему о вычетах, получаем:
