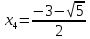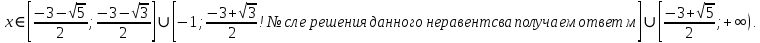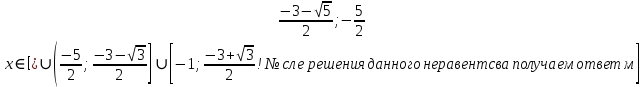Разработать методику обучения учащихся решению неравенств определенного вида (по выбору), которая должна отвечать следующим требованиям:
1. Тематическое планирование (на 3-5 уроков с указанием их типов). 1
2. Конспект 1 урока по изучению нового материала или систематизации ранее изученного материала. 2
3. Задания для отработки формируемых умений с решениями. 22
4. Проверочная (контрольная) работа, завершающая изучение неравенств данного вида (с решением). 26
1. Тематическое планирование (на 3-5 уроков с указанием их типов).
Тематическое планирование на основе Алгебра и начала математического анализа. Сборник рабочих программ. 10-11 классы: учеб. пособие для общеобразоват. организаций : базовый и углубл. уровни / [сост. Т. А. Бурмистрова]. – 2-е изд., перераб. – М. : Просвещение, 2018. – 143 с.
50
|
Решение логарифмических уравнений.
|
Урок общеметодологической направленности
|
51
|
Решение систем логарифмических уравнений
|
Комбинированный урок
|
52
|
Логарифмические неравенства.
|
Урок открытия новых знаний
|
53
|
Решение логарифмических неравенств.
|
Урок общеметодологической направленности
|
54
|
Урок обобщения систематизации знаний.
|
Урок повторения
|
55
|
Контрольная работа № 4 по теме «Логарифмическая функция».
|
Урок развивающего контроля
|
2. Конспект 1 урока по изучению нового материала или систематизации ранее изученного материала.
Конспект урока
Тема занятия: решение логарифмических неравенств.
Цель занятия: обобщить и систематизировать знания учащихся по теме «Логарифмические неравенства», совершенствовать умение учащихся применять полученные знания при решении задач.
Тип занятия: урок повторения.
Планируемые результаты:
Предметные
- ученик на углубленном уровне получит возможность научиться решать логарифмические неравенства различного типа.
Метапредметные
Регулятивные УУД
- уметь рассуждать и делать выводы при решении задач;
- уметь самостоятельно планировать пути достижения целей, в том числе альтернативные.
Познавательные УУД
- выстраивать логическую цепочку, в ходе достижения цели.
Коммуникативные УУД
-умение организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками;
- высказывать и обосновывать собственное мнение при решении задач;
- формулировать и объяснять свою точку зрения.
Личностные
- осознанное, уважительное и доброжелательное отношение к другому человеку, его мнению;
- готовность и способность вести диалог с другими учащимися и достигать в нем взаимопонимания.
Формы обучения: индивидуальная, групповая.
Методы: словесные, наглядные, практические.
Этап
|
Деятельность учителя
|
Деятельность ученика
|
Примечание
|
Организационный этап
|
|
Ученики присаживаются за рабочие места
|
|
Актуализация знаний
|
С помощью фронтального опроса повторяются понятия необходимые для занятия.
Дать определение логарифма числа?
Сформулируйте основные свойства логарифмов?
Назовите формулу перехода логарифма от одного основания к другому?
Какой вид имеет простейшее логарифмическое неравенство?
Как на решение неравенства влияет основание логарифма?
Назовите основные способы решения логарифмических неравенств, которые вам известны?
|
Логарифмом положительного числа 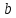 по основанию по основанию 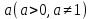 называют число называют число 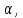 такое, что такое, что 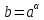 . .
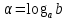
1. Логарифм произведения двух положительных чисел, равен сумме логарифмов этих чисел;
2. Логарифм частного двух положительных чисел, равен разности логарифмов делимого и делителя.
3. Логарифм степени положительного числа равен произведению показателя степени на логарифм этого числа.
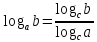
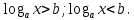
Если основание больше 1, то при решении знак неравенства остается без изменения. Если основание логарифма находится в интервале от 0 до 1, то при решении знак неравенства меняется на противоположный
1. Простейшие неравенства, неравенства, которые решаются с помощью свойств логарифмов;
2. Метод введения новой переменной;
3. Обобщенный метод интервалов;
4. Метод рационализации.
|
|
Мотивационный этап, постановка цели и задач урока
|
Мы продолжаем изучать тему решение логарифмических неравенств. Предложите цель урока, и возможные задачи.
|
Обобщить знания по теме «Логарифмические неравенства», а также совершенствовать умения применять полученные знания при решении задач.
|
|
Фронтальное выполнение заданий
|
Первая часть занятия будет проходить во фронтальной форме. Совместно будут решены задания трёх уровней сложности.
Приглашается второй ученик для решения неравенства среднего уровня сложности.
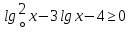
Приглашается третий ученик для решения неравенства повышенного уровня сложности.
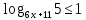
|
Один ученик выходит к доске и решает предложенное неравенство.
Выходит второй ученик для решения неравенства среднего уровня сложности.
Выходит второй ученик для решения неравенства среднего уровня сложности.
|
Решение:
Простейшее логарифмическое неравенство
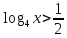
ОДЗ: 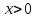
Так как 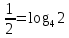 , то , то
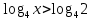
Так как основание больше 1, то функция 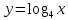 возрастающая, значит, логарифмическое неравенство сводится к неравенству вида: возрастающая, значит, логарифмическое неравенство сводится к неравенству вида: 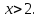
Согласуем решение неравенства с ОД.
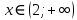 . .
Ответ: 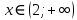 . .
Решение:
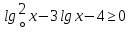
ОДЗ: 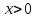
Введем новую переменную 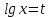
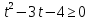
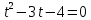
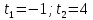
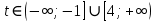 . .
Сделаем обратную подстановку и так же сразу учтем ОДЗ:
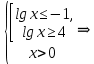 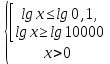 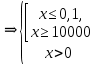
Согласуем с ОДЗ
Ответ: 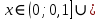
Решение:
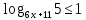
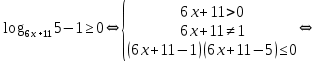
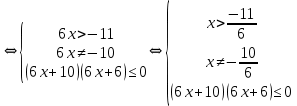
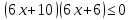
Решим методом интервалов:
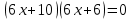 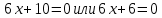 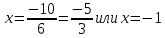
Ответ: 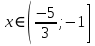
|
Индивидуальное выполнение заданий
|
У вас есть карточки трёх цветов: зелёный, жёлтый и красный. На этих карточках для решения предложены логарифмические неравенства. Самая первая карточка зеленого цвета, содержит несколько простейших логарифмических неравенства. Вторая карточка желтого цвета – содержит логарифмические неравенства среднего уровня. Третья карточка красного цвета – включает в себя два логарифмических неравенства повышенного уровня сложности. Ваша задача состоит в том, чтобы выбрать уровень сложности и решить неравенства верно. В соответствии с выбранным уровнем вам будут выставлены отметки. Зелёный – «3», Жёлтый – «4», Красный – «5»
|
Решают неравенства из карточек (Приложение 1)
Решение предложено в приложении 2.
|
|
Работа в группах
|
Вы сдали свои работы, их я проверю позже. Теперь вам необходимо разделиться на группы, на 5 по 4 человека.
И попытаться решить неравенство:
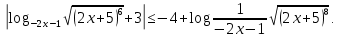
|
Внутри групп идет обсуждение, каким способом необходимо решать данное неравенство.
После того, как каждая группа решит неравенство, начинается этап обсуждения, учащиеся могут совещаться, сравнивать решения, высказываться свою точку зрения и доказывать ее.
|
Если у групп возникли различные методы решения неравенства, то к доске приглашаются по одному представителю от каждой группы, чтобы продемонстрировать свое решение. Если метод решения у групп совпал, ученик одной из групп приглашается к доске для решения.
Решение предложено в приложении 3.
|
Рефлексия
|
Анализируя свою деятельность на уроке, оцените её, подняв карточку соответствующего цвета. Зелёный – не доволен работой или доволен частично, жёлтый – работа на уроке была достаточно продуктивной, красный – я справился со всеми заданиями очень хорошо. Если у вас есть какие-то идеи или мысли об уроке можете их высказать.
|
Поднимают карточки, анализируют свою работу.
|
|
Подведение итогов
|
Чем мы сегодня занимались на уроке?
Домашнее задание: посмотреть и проанализировать записи в тетради.
|
Отрабатывали навыки решения логарифмических неравенств;
Выполняли индивидуальное задание по решению логарифмических неравенств;
Работали в группах;
Рассматривали трудное неравенство и искали пути его решения.
|
|
Приложение 1
Зелёный уровень
1. 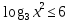
2. 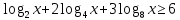
|
Жёлтый уровень
1. 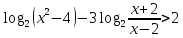
2. 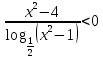
|
Красный уровень
1.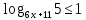
2. 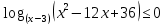
|
Приложение 2
Зелёный уровень
1. 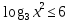
ОДЗ: 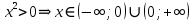 . .
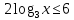
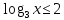
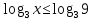
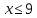
Согласуем с ОДЗ:
Ответ: 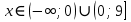 . .
2. 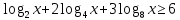
ОДЗ: 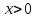
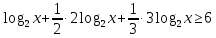
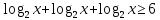
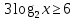
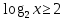
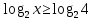
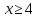
Согласуем с ОДЗ
Ответ: 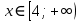 . .
|
Жёлтый уровень
1. 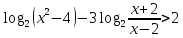
ОДЗ: 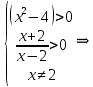 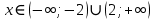
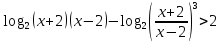
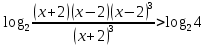
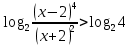
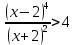
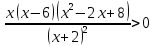
После решения неравенства получаем ответ: 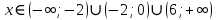 . .
Теперь необходимо согласовать полученный результат с ОДЗ.
Ответ: 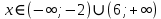
2. 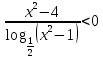
ОДЗ: 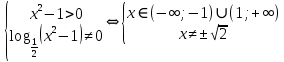
Перейдем к равносильному неравенству:
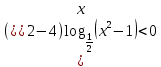
Находим нули функции:
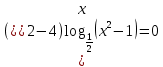
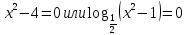
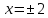 или или 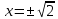
После учета ОДЗ образовались следующие промежутки:
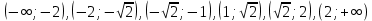
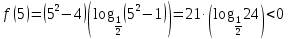
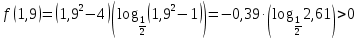
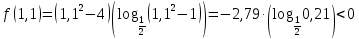
…
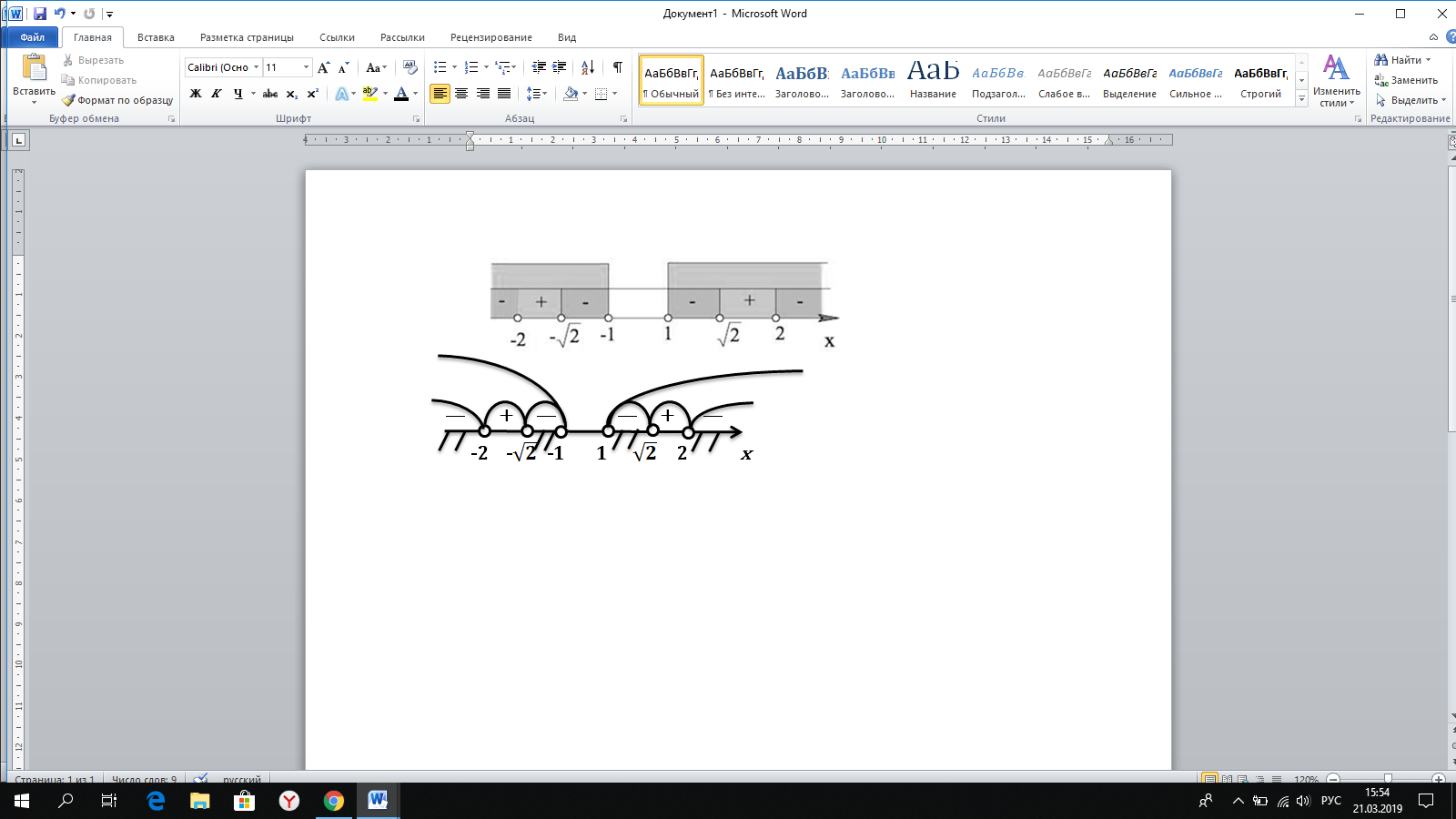
Ответ: 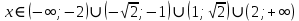
|
Красный уровень
1.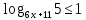
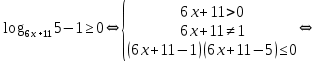
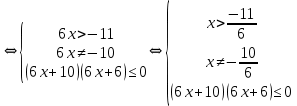
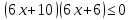
Решим методом интервалов:
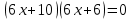 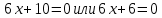 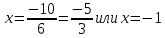
Ответ: 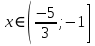
2. 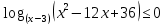
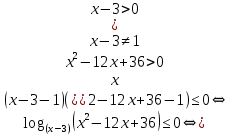
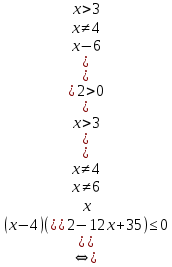
Решим методом интервалов:
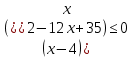
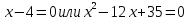
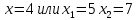
Ответ: 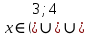
|
Приложение 3
Решите неравенство:
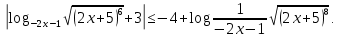
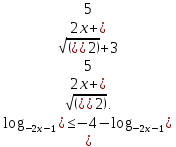
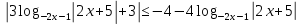
Введем замену: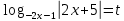
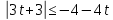
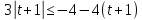
Для того чтобы проще было работать с этим неравенством введем еще одну замену: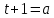
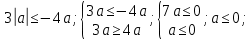
Обратная замена: 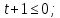
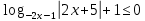
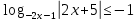
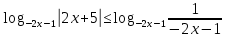
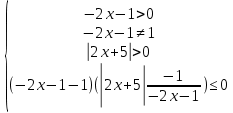
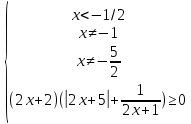
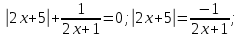
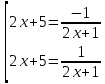
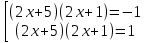
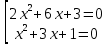
Находим корни каждого уравнения из данной совокупности
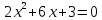
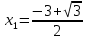 , , 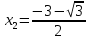
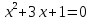
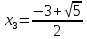 , , 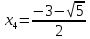
После решения данного неравенства получаем ответ 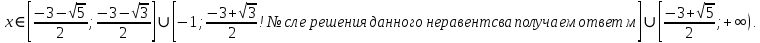
Ответ: 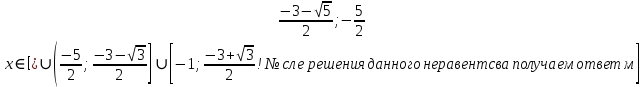
|
3. Задания для отработки формируемых умений с решениями.
А1. Укажите наибольшее из данных чисел: 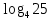 , , 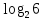 , , 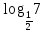 , , 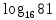 . .
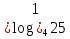 , 2) , 2) 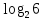 , , 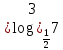 , , 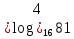 . .
Решение:
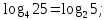
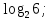
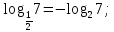
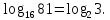
Наибольшим из данных чисел является 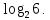
Ответ: 2)
A2. Решите неравенство 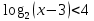
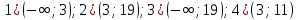
Решение:
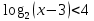
ОДЗ: 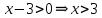
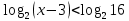
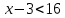
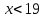
Согласуем с ОДЗ
Ответ: 2)
A3. Укажите наименьшее целое решение неравенства 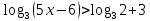
12; 2) 10; 3) 13; 4) 23
Решение:
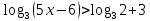
ОДЗ: 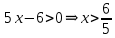
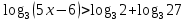
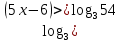
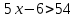
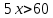
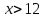
Согласуем с ОДЗ
Наименьшим целым решением неравенства является число 12.
Ответ: 3)
A4. Решите неравенство 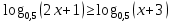
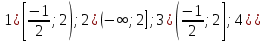
Решение:
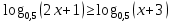
ОДЗ: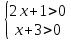 , , 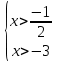 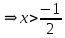
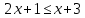
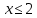
Согласуем с ОДЗ
Ответ: 3)
B1. Найдите сумму наименьшего целого положительного и наибольшего целого отрицательного решений неравенства 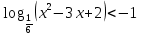
Решение:
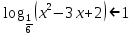
ОДЗ: 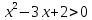 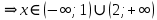
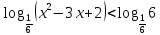
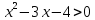
После решения этого неравенства получаем ответ:
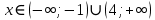
Согласуем с ОДЗ:
Ответ: 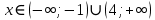 . .
Наименьшее целое положительно решение это 5, наибольшее целое отрицательное -2.
5+(-2)=3
Ответ: 3
B2. Решите неравенство 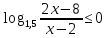
Решение:
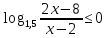
ОДЗ: 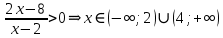
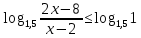
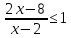
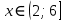
Согласуем с ОДЗ:
Ответ: 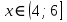
B3. Укажите наименьшее целое решение неравенства 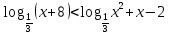
Решение:
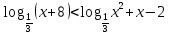
ОДЗ: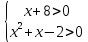 , , 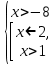 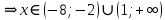
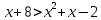
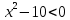
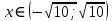
Согласуем с ОДЗ:
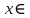 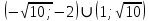
Наименьшим целым решением будет число -3.
Ответ: -3
C1. Решите неравенство 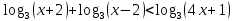
Решение:
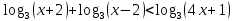
ОДЗ: 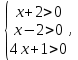 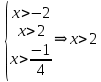
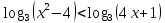
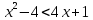
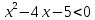
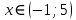
Согласуем с ОДЗ:
Ответ: 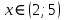
C2. Решите неравенство 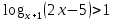
Решение:
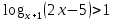
ОДЗ: 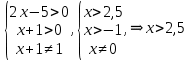
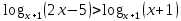
Метод рационализации
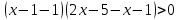
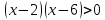
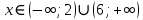
Согласуем с ОДЗ:
Ответ: 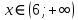
C3. Решите неравенство 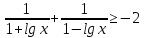
Решение:
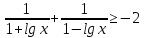
ОДЗ: 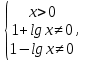 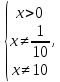
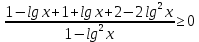
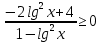
После решения данного неравенства получаем ответ 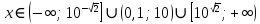 . .
Согласуем с ОДЗ:
Ответ: 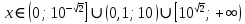 . .
4. Проверочная (контрольная) работа, завершающая изучение неравенств данного вида (с решением).
Критерии
Выполнено 100% - отметка «5»
Выполнено 80% отметка «4»
Выполнено 60% отметка «3»
Выполнено менее 50% – «2»
Решить неравенство 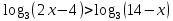
Решить неравенство 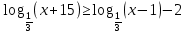
Решить неравенство 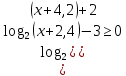
Решить неравенство 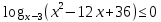
Решить неравенство 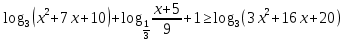
  |
 Скачать 0.61 Mb.
Скачать 0.61 Mb. ,
,  ,
,  ,
, 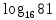 .
.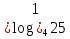 , 2)
, 2) 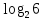 ,
, 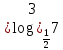 ,
, 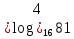 .
.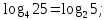
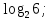
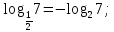
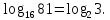
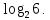
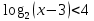
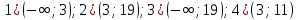
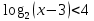
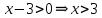
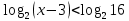
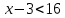
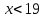
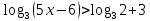
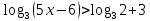
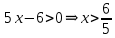
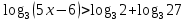
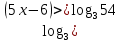
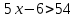
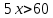
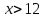
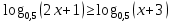
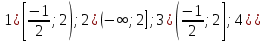
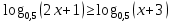
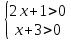 ,
, 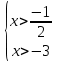
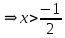
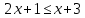
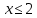
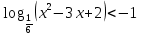
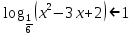
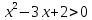
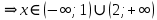
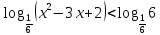
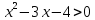
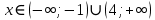
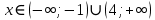 .
.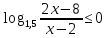
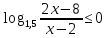
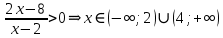
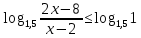
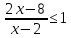
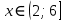
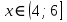
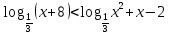
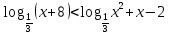
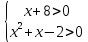 ,
, 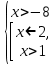
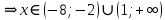
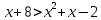
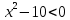
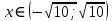
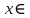
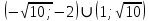
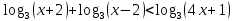
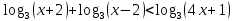
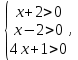
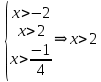
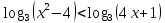
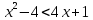
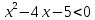
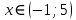
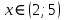
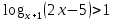
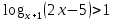
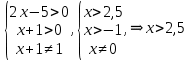
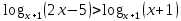
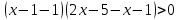
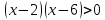
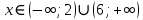
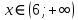
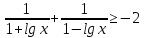
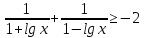
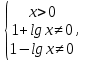
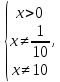
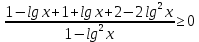
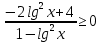
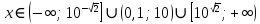 .
.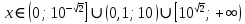 .
.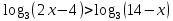
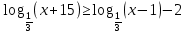
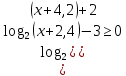
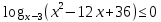
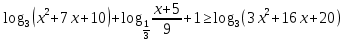



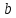 по основанию
по основанию 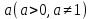 называют число
называют число 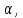 такое, что
такое, что 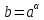 .
.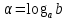
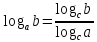
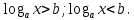
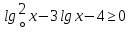
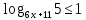
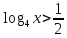
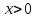
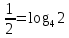 , то
, то 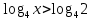
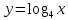 возрастающая, значит, логарифмическое неравенство сводится к неравенству вида:
возрастающая, значит, логарифмическое неравенство сводится к неравенству вида: 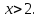
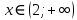 .
.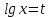
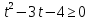
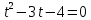
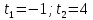
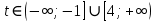 .
.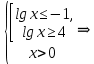
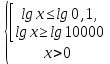
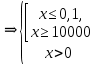
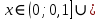
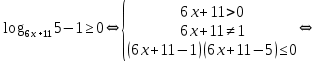
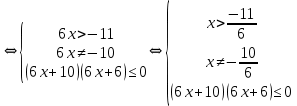
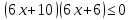
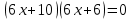
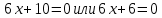
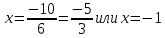
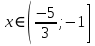
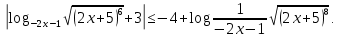
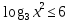
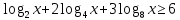
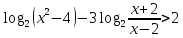
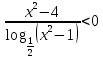
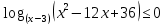
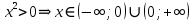 .
.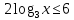
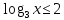
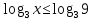
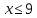
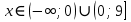 .
.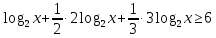
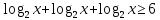
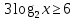
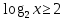
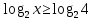
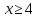
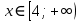 .
.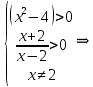
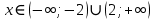
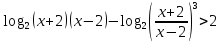
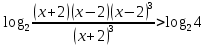
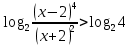
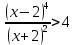
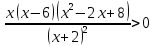
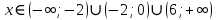 .
.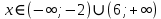
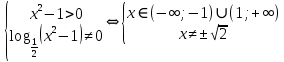
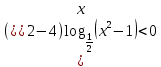
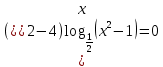
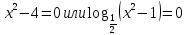
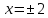 или
или 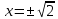
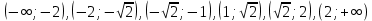
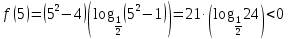
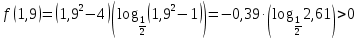
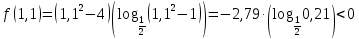

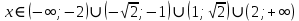
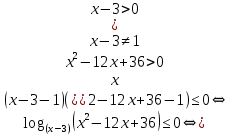
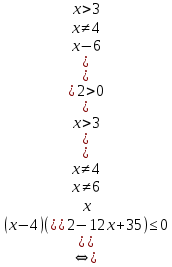
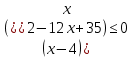
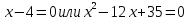
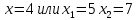
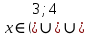
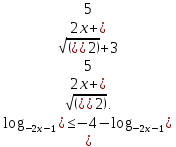
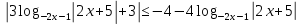
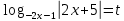
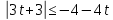
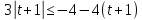
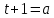
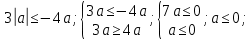
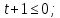
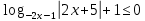
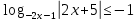
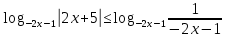
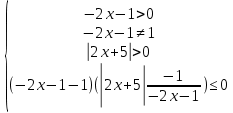
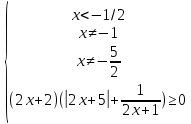
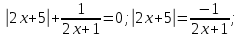
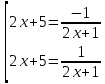
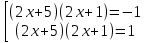
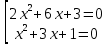
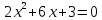
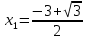 ,
, 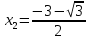
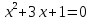
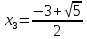 ,
,