Танатаров.Ш.М отчёт по практике. Теодолитная съемка
 Скачать 239.96 Kb. Скачать 239.96 Kb.
|
|
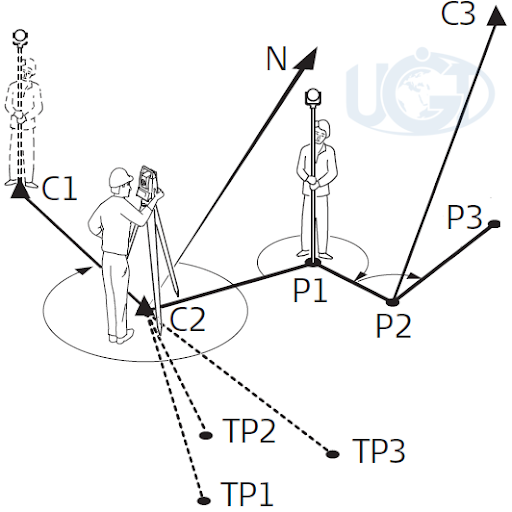
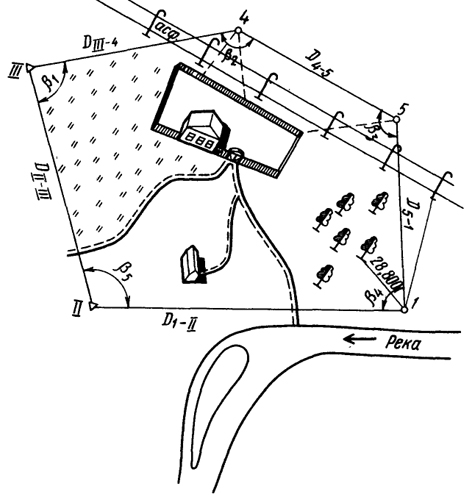
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РЕСПУБЛИКИ КАЗАХСТАН «АТЫРАУСКИЙ УНИВЕРСИТЕТ НЕФТИ И ГАЗА ИМЕНИ САФИ УТЕБАЕВА» КеАҚ  Факультет «Нефти и газ» Кафедра «Геология и геофизика» ОТЧЁТ ПО ПРАКТИКЕ Тема: Теодолитная съемка Выполнил:Танатаров.Ш.М Группа: ГК-18/1 к/о Проверил(-а):Ежирова.А.У Атырау 2020 год Содержание Введение…………………………………………………………………………...3 Глава 1. Теория……...……………………………………...……………………...4 1.1 Теодолитная съемка ………………. .………………………………………....4 1.2 Вычисление координат пунктов замкнутого теодолитного хода………………. .……………………………………………………………....6 Глава 2. Схемы…………………………………………………………………….9 2.1 Схемы.Таблицы.Приложении………….…………………………………….9 Заключение……………………………………………………………………….15 Список литературы…………………………………………………………….16 ВведениеГеодезия - одна из древнейших наук. Слово «геодезия» образовано из двух слов - «земля» и «разделяю», а сама наука возникла как результат практической деятельности человека по установлению границ земельных участков, строительству оросительных каналов, осушению земель. Полевая учебная геодезическая практика является завершающим этапом изучения курса инженерной геодезии. На нее отводится значительная часть учебного времени. Практику проходил в г. Актау на территории учебного корпуса Ш.Есенов, расположенного на 32 микрорайоне. Целью практики является приобретение навыков работы на местности с приборами, их использование и обработка полученной информации. Перед практикой ставятся следующие задачи: Закрепление и углубление знаний. Освоение новейших геодезических приборов. Дальнейшее развитие практических навыков в процесса самостоятельного выполнения геодезических измерений, последующей их математической обработки и оценки точности. I глава1.1 Теодолитная съемкаТеодолитную съемку я выполнил на территории Каспийский технологический университет имени Шахмардана Есенова(32 микрорайон). Теодолитная съемка выполнялась в два этапа: 1.Полевой. Камеральный 1)Полевой этап. В процессе проведения этого этапа, мною была выполнена рекогносцировка местности ( визуальный осмотр), в которой были намечены точки стояния теодолита. После этого я приступил к съемке местности. Съемки выполнялись электронным теодолитом ТЕО20. Проложение теодолитного хода заключалось в измерении горизонтальных углов и расстоянии между точками. Углы измерялись способом «полный прием» (т.е. при круге левом и при круге правом).Для дальнейшей обработки определялось среднее значение угла. Расстояние между точками измерялось рулеткой в двух направлениях: прямое и обратное. Все это отобразили в полевом журнале. После этого я приступил к съемке контуров, при этом использовал следующие методы: o метод перпендикуляров o угловых засечек o линейных засечек в процессе съемки вели абрис. (Абрис - схематические изображения объекта на каждый точке полигона.). 2.Камеральный этап. После окончания полевых работ я приступил к камеральной обработке. Камеральная обработка начинается с вычисления ведомости координат. Из полевого журнала в графу 3 (измеренный угол) я выписал среднее значение измеренных углов, затем нашел их сумму. Она составила: ∑теоритическая. = 540 ∑практическая. = 5401,40 Далее я увязал углы, невязку разбросал с обратным знаком. По увязанным углам и дирекционному углу я рассчитал дирекционный углы других линий. Далее нашёл румбы и вычислил приращения координат. Рассчитал координаты точек полигона. 1.2 Вычисление координат пунктов замкнутого теодолитного хода. Вычисляют угловую невязку fβ замкнутого теодолитного хода fβ =Ʃβизм- Ʃβтеор, где Ʃβизм – сумма измеренных углов; Ʃβтеор – теоретическая сумма внутренних углов замкнутого теодолитного хода, Ʃβтеор = 180°(n-2); n – число углов теодолитного хода. В приводимом примере угловая невязка fβ = +01,40ʹ. Сравниваю найденную угловую невязку fβ с предельно допустимой невязкой f Vi = (-fβ)/n. Однако часто полученная невязка не делится на число углов без остатка. В этом случае большее значение поправки вводят в углы, образованные короткими сторонами. В моем случае невязка поделилась поровну и составила -0,20ʹ. Сумма поправок, вводимых во все углы замкнутого теодолитного хода, должна равняться невязке fβ с противоположным знаком: Ʃvi = -fβ. Вычисляю исправленные углы. Для этого к измеренному углу прибавляю поправку с учетом ее знака: βисп = βизм+viПроверяю равенство суммы исправленных углов и теоретической суммы углов замкнутого хода (Ʃβисп=Ʃβтеор), что позволяет проконтролировать правильность увязки углов. В рассматриваемом примере Ʃβисп=Ʃβтеор=540°00,0ʹ. Вычисляю дирекционные углы сторон замкнутого теодолитного хода по дирекционному углу исходной стороны 1-2 и увязанным углам βисп: αn+1 = αn + 180° - βn,n+1, где αn+1 – дирекционный угол последующей стороны; αn – дирекционный угол предыдущей стороны; βn,n+1 - исправленный угол, вправо по ходу лежащий между предыдущей и последующей сторонами. Сначала вычислила дирекционные углы сторон привязочного хода и стороны Ӏ-ӀӀ замкнутого хода, используя измеренные вправо по ходу лежащие углы привязочного хода. Величины дирекционных углов должны быть положительными и находиться в пределах от 0°00,0ʹ до 359°59,9ʹ. Поэтому при вычислениях иногда приходится прибавлять или вычитать 360°. Затем вычисляю дирекционные углы остальных сторон замкнутого хода. В замкнутом ходе контролем вычислений является получение дирекционного угла стороны Ӏ-ӀӀ(αI-II), с которого начинались вычисления: Вычисленные значения дирекционных углов занесла в графу Перевожу дирекционные углы в румбы и записываю в графу . Для упрощения дальнейших вычислений значения румбов желательно округлить до целых минут. Вычисляю приращения координат ∆Х и ∆Y по значениям горизонтальных проложений d и дирекционным углам α или румбам r сторон теодолитного хода: ∆Х = d cos α = ± d cos r, ∆Y = d sin α = ± d sin r. Определяю невязки в приращениях координат fx и fyпо осям X и Y: fx = Ʃ∆Xвыч , fY = Ʃ∆Yвыч , где Ʃ∆Xи Ʃ∆Y- суммы вычисленных приращений координат замкнутого хода. В данном случае fx = -0,02 м, fy = +0,00 м. Если относительная невязка допустима, то вычисленные приращения увязывают, вводя в них поправки. Поправки имеют знаки, обратные знакам невязок fxи fy,а их величины пропорциональны длинам сторон. Поправки вычисляют с округлением до 0,01 м и записывают в графы 10 и 11 ведомости. Сумма поправок должна равняться невязке с противоположным знаком. Найдя исправленные приращения, складываю алгебраически величины вычисленных приращений с их поправками. Алгебраическая сумма исправленных приращений координат по каждой оси должна быть равна нулю. Координаты вершин замкнутого теодолитного хода вычисляю по формулам: Xn+1 = Xn + ∆Xn,n+1, Yn+1 = Yn + ∆Yn,n+1, где Xn+1, Yn+1- абсцисса и ордината последующей вершины теодолитного хода; Xn , Yn-абсцисса и ордината предыдущей вершины теодолитного хода; ∆Xn,n+1, ∆Yn,n+1 - исправленные приращения координат между предыдущей и последующей вершинами. Вычисленные координаты занесла в графы и ведомости. Контролем правильности вычисления координат замкнутого хода является получение абсциссы и ординаты точки Ӏ хода по координатам точки V и приращениям координат между этими точками. После этого я приступил к построению теодолитного хода. Для этого я вычертил координатную сетку (М 1:500). По полученным координатам нанес все точки теодолитного хода. II глава 2.1 Схемы.Таблицы.Приложении Полевые работы: съемка ситуации на местности замкнутого контура
Вычисление координат замкнутого теодолитного хода
Дирекционные углы: 3-4=2-3+180-3=5743’+180-86=15143’ 4-1=3-4+180-4=15143’+180-9411’=23732’ 1-2=4-1+180-1=23732’+180-89=32832’ 2-3=1-2+180-2=32832’+180-9049’=41743’-360=5743 II Румбы: rю.в.=180-3-4=180-15143’=2817’ rю.з.=4-1-180=23732’-180=5732’ rс.з=360-1-2=360-32832’=3128’ III. Вычисление приращение координат: x=d*cos 3-4=49,7*cos 15143’= -43,67 x=d*cos 4-1=49,9*cos 23732’= -25,84 x=d*cos 1-2=47,6*cos 32832’= 41,5 x=d*cos 2-3=50*cos 5743’= 27,91 y=d*sin 3-4=49,7*sin 15143’= 23,76 y=d*sin 4-1=49,9*sin 23732’= -41 y=d*sin 1-2=47,6*sin 32832’= -24,99 y=d*sin 2-3=50*sin 5743’= 42,13 y=d*sin 2-3=50*sin 5743’= 42,13 IV Уравнивание приращений: Находим поправку для ∱x на 1 м ∱x= 25/(25 +41+27+43)= 0,18 м xI-II=0,18*25=4,54 м xII-III=0,18*41=7,35 6 м xIII-IV=0,18*27=4,864 м xIV-I=0,18*43=8,74 9 м Находим поправку для ∱y на 1 м ∱y=10/(41 +24+42+23)= 0,07 м yI-II=0,07*41=2,87 3 м yII-III=0,07*24=1,68 2 м yIII-IV=0,07*42=2,943 м V. Вычисление координат теодолитного хода: Берем произвольных две координаты х=200, y=300 И вычисляем последовательно: xn=xn-1+x yn=yn-1+y Контроль по последнее точке, мы должны обратно вернуться к начальным координатам, т.е. х=200, y=300 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||