Теорема сложения( сумма вероятностей)
|
Теорема умножения(произведение вероятностей)
|

42.Вероятность того, что на тесте по биологии учащийся О. верно решит больше 11 задач, равна 0,67. Вероятность того, что О. верно решит больше 10 задач, равна 0,74. Найдите вероятность того, что О. верно решит ровно 11 задач. Решение: Рассмотрим события A = «учащийся решит 11 задач» и В = «учащийся решит больше 11 задач». Их сумма — событие A + B = «учащийся решит больше 10 задач». События A и В несовместные, вероятность их суммы равна сумме вероятностей этих событий: P(A + B) = P(A) + P(B). Тогда, используя данные задачи, получаем: 0,74 = P(A) + 0,67, откуда P(A) = 0,74 − 0,67 = 0,07.Ответ: 0,07.
43.Чтобы поступить в институт на специальность «Лингвистика», абитуриент должен набрать на ЕГЭ не менее 70 баллов по каждому из трёх предметов — математика, русский язык и иностранный язык. Чтобы поступить на специальность «Коммерция», нужно набрать не менее 70 баллов по каждому из трёх предметов — математика, русский язык и обществознание. Вероятность того, что абитуриент З. получит не менее 70 баллов по математике, равна 0,6, по русскому языку — 0,8, по иностранному языку — 0,7 и по обществознанию — 0,5.Найдите вероятность того, что З. сможет поступить хотя бы на одну из двух упомянутых специальностей.
Решeние: Для того, чтобы поступить хоть куда-нибудь, З. нужно сдать и русский, и математику как минимум на 70 баллов, а помимо этого еще сдать иностранный язык или обществознание не менее, чем на 70 баллов. Пусть A, B, C и D — это события, в которых З. сдает соответственно математику, русский, иностранный и обществознание не менее, чем на 70 баллов. Тогда поскольку
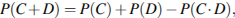 для вероятности поступления имеем: для вероятности поступления имеем:
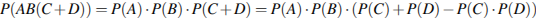
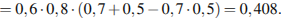
Из районного центра в деревню ежедневно ходит автобус. Вероятность того, что в понедельник в автобусе окажется меньше 20 пассажиров, равна 0,94. Вероятность того, что окажется меньше 15 пассажиров, равна 0,56. Найдите вероятность того, что число пассажиров будет от 15 до 19. Решeние: Рассмотрим события A = «в автобусе меньше 15 пассажиров» и В = «в автобусе от 15 до 19 пассажиров». Их сумма — событие A + B = «в автобусе меньше 20 пассажиров». События A и В несовместные, вероятность их суммы равна сумме вероятностей этих событий: P(A + B) = P(A) + P(B). Тогда, используя данные задачи, получаем: 0,94 = 0,56 + P(В), откуда P(В) = 0,94 − 0,56 = 0,38. Ответ: 0,38.

Задачи на правила сложения и умножения вероятностей.
В разделах, касающихся использования формул и правил комбинаторики, я неоднократно упоминала правила умножения и правила сложения вариантов, называя их И-правилом и ИЛИ-правилом. Этот же подход можно распространить на правила теории вероятностей.
Правило сложения вероятностей: если A и В несовместимые события, то вероятность того, что наступит хотя бы одно из двух событий А или В, равна сумме их вероятностей.
P(A + B) = P(A) + P(B)
Правило умножения вероятностей: если A и В независимые события, то вероятность одновременного наступления обоих событий А и В, равна произведению их вероятностей.
P(A·B) = P(A) · P(B)
Обратите внимание:
Мы говорим о сумме событий, когда может наступить хотя бы одно из двух событий или А, или В, или оба вместе. Но приведенную формулу применяем только для несовместимых событий, т.е. в случае, если они не могут произойти вместе. Например, не может один ученик писать экзамен сразу в двух аудиториях.
Мы говорим о произведении событий при наступлении и А, и В одновременно. Но приведенную формулу применяем только для независимых событий, когда результат одного из них не связан с результатом другого. Например, при бросании двух игральных костей ни одна из них "не знает", какое число очков выпало на другой.
Если указанные условия не выполняются, то правила сложения и умножения вероятностей приобретают более сложный вид.
Правило сложения вероятностей для совместимых событий: вероятность суммы двух совместимых событий равна сумме их вероятностей за вычетом вероятности их произведения.
P(A + B) = P(A) + P(B) − P(A·B)
Правило умножения вероятностей для зависимых событий: вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого при условии, что первое событие произошло.
P(A·B) = P(A) · P(B/A)
Но в любом случае, правило сложения вероятностей используем там, где перед описанием события в тексте задачи можно вставить союз "или", поэтому называем его ИЛИ-правилом. Правило умножения вероятностей используем там, где перед описанием события в тексте задачи можно вставить союз "и", поэтому называем его И-правилом. Давайте посмотрим, как это работает на примере задачи о ковбое.
Пример 1
Ковбой Джон попадает в муху на стене с вероятностью 0,9, если стреляет из пристрелянного револьвера. Если Джон стреляет из непристрелянного револьвера, то он попадает в муху с вероятностью 0,2. На столе лежит 10 револьверов, из них только 4 пристрелянные. Ковбой Джон видит на стене муху, наудачу хватает первый попавшийся револьвер и стреляет в муху. Найдите вероятность того, что Джон промахнётся.
Запишем, как могло случиться, что "Джон промахнулся".
"Ковбой схватил пристрелянный револьвер И не попал в муху, ИЛИ ковбой схватил непристрелянный револьвер И не попал в муху."
Сначала разберемся с пистолетами:
- Вероятность схватить пристрелянный пистолет равна 4/10 = 0,4. Мы вычислили её по определению вероятности: здесь один пистолет = одно элементарное событие, один пристрелянный пистолет = одно благоприятствующее событие.
- Вероятность схватить непристрелянный пистолет равна (10−4)/10 = 0,6. Вычислили аналогично, определив число непристрелянных пистолетов.
Затем разберемся с мухой:
- Если ковбой стрелял из пристрелянного револьвера, то он НЕ попал в муху с вероятностью 1−0,9=0,1.
- Если ковбой стрелял из непристрелянного револьвера, то он НЕ попал в муху с вероятностью 1−0,2=0,8.
Здесь мы воспользовались формулой для вероятности противоположного события, потому что в условии даны вероятности попадания в муху из разных пистолетов, но не промахов.
Теперь вернемся к нашей формулировке события "Ковбой схватил..." и вместо текста, описывающего составляющие события, подставим полученные числа - их вероятности, а вместо союзов "И" и "ИЛИ" знаки "·" и "+" соответственно. Получаем:
0,4·0,1 + 0,6·0,8 = 0,04 + 0,48 = 0,52.
Задача 1
На экзамене по геометрии школьнику достаётся один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос на тему «Вписанная окружность», равна 0,2. Вероятность того, что это вопрос на тему «Параллелограмм», равна 0,15. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.
Ответ: 0,35
Задача 2
Если гроссмейстер А. играет белыми, то он выигрывает у гроссмейстера Б. с вероятностью 0,52. Если А. играет черными, то А. выигрывает у Б. с вероятностью 0,3. Гроссмейстеры А. и Б. играют две партии, причем во второй партии меняют цвет фигур. Найдите вероятность того, что А. выиграет оба раза. Ответ: 0,156
Задача 3
В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,3. Вероятность того, что кофе закончится в обоих автоматах, равна 0,12. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.
 Ответ: 0,52 Ответ: 0,52
|


На фабрике керамической посуды 10% произведённых тарелок имеют дефект. При контроле качества продукции выявляется 80% дефектных тарелок. Остальные тарелки поступают в продажу. Найдите вероятность того, что случайно выбранная при покупке тарелка не имеет дефектов. Ответ округлите до сотых. Решение: Пусть завод произвел  тарелок. В продажу поступят все качественные тарелки и 20% невыявленных дефектных тарелок: тарелок. В продажу поступят все качественные тарелки и 20% невыявленных дефектных тарелок: 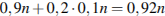 тарелок. Поскольку качественных из них тарелок. Поскольку качественных из них 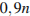 , вероятность купить качественную тарелку равна 0,9п :0,92п=0,978 Ответ: 0,978. , вероятность купить качественную тарелку равна 0,9п :0,92п=0,978 Ответ: 0,978.
По отзывам покупателей Иван Иванович оценил надёжность двух интернет-магазинов. Вероятность того, что нужный товар доставят из магазина А, равна 0,8. Вероятность того, что этот товар доставят из магазина Б, равна 0,9. Иван Иванович заказал товар сразу в обоих магазинах. Считая, что интернет-магазины работают независимо друг от друга, найдите вероятность того, что ни один магазин не доставит товар. Решение: Вероятность того, что первый магазин не доставит товар равна 1 − 0,9 = 0,1. Вероятность того, что второй магазин не доставит товар равна 1 − 0,8 = 0,2. Поскольку эти события независимы, вероятность их произведения (оба магазина не доставят товар) равна произведению вероятностей этих событий: 0,1 · 0,2 = 0,02


 
Задание 4. На фабрике керамической посуды 30% произведённых тарелок имеют дефект. При контроле качества продукции выявляется 60% дефектных тарелок. Остальные тарелки поступают в продажу. Найдите вероятность того, что случайно выбранная при покупке тарелка не имеет дефектов. Ответ округлите до сотых.
Решение.
Из условия задачи следует, что из 30% бракованных тарелок, выявляется только 60%, т.е. 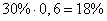 брака от всего объема произведенных тарелок. В продажу поступает брака от всего объема произведенных тарелок. В продажу поступает 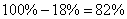 тарелок и среди них бракованных тарелок и среди них бракованных 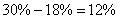 . Таким образом, вероятность того, что случайно выбранная тарелка не будет иметь дефектов, равна . Таким образом, вероятность того, что случайно выбранная тарелка не будет иметь дефектов, равна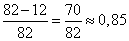 . .
2) На фабрике керамической посуды 20% произведенных тарелок имеют дефект. При контроле качества продукции выявляется 70% дефектных тарелок. Остальные тарелки поступают в продажу. Найдите вероятность того, что случайно выбранная при покупке тарелка не имеет дефектов. Ответ округлите до сотых.
Решение:
Из 20% дефектных тарелок отбраковывается 70%, т.е. доля отбракованных тарелок от общего числа составляет 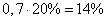 . Соответственно в продажу поступает 100%-14% тарелок и среди них не бракованных 86%-6% тарелок. Следовательно, вероятность покупки тарелки без дефектов будет равна . Соответственно в продажу поступает 100%-14% тарелок и среди них не бракованных 86%-6% тарелок. Следовательно, вероятность покупки тарелки без дефектов будет равна
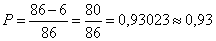
Помещение освещается фонарем с тремя лампами. Вероятность перегорания одной лампы в течение года равна 0,3. Найдите вероятность того, что в течение года хотя бы одна лампа не перегорит.
Решение:
Данную задачу проще решать от обратного, т.е. сначала найти вероятность перегорания всех ламп, а затем, вычислить противоположную вероятность, которая и будет ответом данной задачи.
Так как одна лампа перегорает в течение года с вероятностью 0,3, то три лампы перегорят с вероятностью 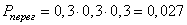
тогда вероятность того, что не перегорит хотя бы одна лампа, равна
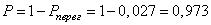 Помещение освещается фонарём с тремя лампами. Вероятность перегорания одной лампы в течение года равна 0,17. Найдите вероятность того, что в течение года хотя бы одна лампа не перегорит. (Решается аналогично прототипу) Помещение освещается фонарём с тремя лампами. Вероятность перегорания одной лампы в течение года равна 0,17. Найдите вероятность того, что в течение года хотя бы одна лампа не перегорит. (Решается аналогично прототипу)
Помещение освещается фонарём с двумя лампами. Вероятность перегорания лампы в течение года равна 0,3. Найдите вероятность того, что в течение года хотя бы одна лампа не перегорит. Решение:
Найдем вероятность того, что перегорят обе лампы. Эти события независимые, вероятность их произведения равно произведению вероятностей этих событий: 0,3·0,3 = 0,09.
Событие, состоящее в том, что не перегорит хотя бы одна лампа, противоположное. Следовательно, его вероятность равна 1 − 0,09 = 0,91.
Ответ: 0,91
Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика выпускает 30% этих стекол, вторая – 70%. Первая фабрика выпускает 3% бракованных стекол, а вторая – 4%. Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.
Решение:
Покупая наугад стекло, покупатель с вероятностью 0,3 купит стекло первой фабрики, и с вероятностью 0,7 – второй фабрики. В результате бракованное стекло можно выбрать из двух возможных исходов:
A: когда выбрали стекло первой фабрики и оно оказалось бракованным
или
B: когда выбрали стекло второй фабрики и оно оказалось бракованным.
Вероятность первого исхода равна
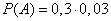
т.к. 3% брака дают долю в 0,03. Вероятность второго исхода
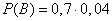
т.к. вторая фабрика производит 4% брака. Вероятность что произойдет или событие A или событие B равна сумме вероятностей этих событий:
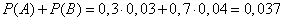 Ответ: 0,037. Ответ: 0,037.
Всем пациентам с подозрением на гепатит делают анализ крови. Если анализ выявляет гепатит, то результат анализа называется положительным. У больных гепатитом пациентов анализ дает положительный результат с вероятностью 0,9. Если пациент не болен гепатитом, то анализ может дать ложный положительный результат с вероятностью 0,02. Известно, что 66% пациентов, поступающих с подозрением на гепатит, действительно больны гепатитом. Найдите вероятность того, что результат анализа у пациента, поступившего в клинику с подозрением на гепатит, будет положительным.
Решение:
Из всех пациентов, поступивших в клинику, 66% действительно больны гепатитом, а 34% - не больны. Положительный результат на гепатит может появиться при двух событиях:
A: пациент действительно болен (вероятность 0,66) и анализ дал положительный результат (вероятность 0,9);
B: пациент не болен (вероятность 0,34), но анализ дал положительный результат (вероятность 0,02).
Найдем вероятность первого события
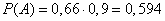
и вероятность второго
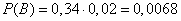 . .
Сумма этих двух вероятностей даст искомое решение задачи:
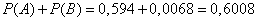 Ответ: 0,6008. Ответ: 0,6008.
|
комбинаторика
|
разное
|


Правило умножения
Одним из основных правил комбинаторики применяемых для решения комбинаторных задач является правило умножения.
Правило умножения (принцип умножения, правило "и"):
пусть имеется две группы элементов,
если элемент из первой группы можно выбрать k1 способами,
после чего элемент из второй группы – k2 способами,
то общее число комбинаций N из двух элементов будет N = k1k2
Пример 1. В группе 14 юношей и 10 девушек. Сколько пар можно составить, чтобы на вечеринке все ребята перетанцевали со всеми девушками?
Решение: Очевидно, число групп равно двум, (т.к. составляем пары)
k1=14 ( т.к. для выбора элемента первой группы имеется 14 вариантов),
k2=10 (т.к. для выбора элемента второй группы имеется 10 вариантов ),
Согласно правила умножения, получаем общее количество различных вариантов: N = k1k2 = 14*10 = 140 пар.
Замечание. Если в качестве первого элемента взять девушку, то ответ не изменится: от перестановки множителей произведение не меняется!
Покажем, что правило умножения допускает обобщение на случай nгрупп элементов:
N = k1k2···kn
И частный случай, когда k1 = k2 =···= kn N = kn
Пример 2. На следующий день после вечеринки та же группа в полном составе (24 человека) пришла на рейтинговую контрольную работу. По ней выставляются не оценки, а распределяются места по рейтингу: 1-е, 2-е и т. д. до последнего. Сколько различных вариантов
первых трёх мест существует?
Решение: Определяем число групп - очевидно число групп равно трем, т.к. число призовых мест равно трем.
k1=24 ( т.к. для выбора лучшей работы имеется 24 варианта),
k2=23 (т.к. для выбора второй работы имеется 23 варианта ),
k3=22 (т.к. для выбора третьей работы имеется 22 варианта).
Согласно правила умножения, получаем общее количество различных вариантов:
N = k1k2k3= 24*23*22 = 12144
Пример 3. Сколько трехзначных четных чисел можно составить из цифр 0, 1, 2, 3, 4, 5, 6, если цифры могут повторяться?
Решение: Определяем число групп - очевидно число групп равно трем, т.к. числа трехзначные.
k1=6 (т.к. в качестве первой цифры можно взять любую цифру из 1, 2, 3, 4, 5, 6),
k2=7 (т.к. в качестве второй цифры можно взять любую цифру из 0, 1, 2, 3, 4, 5, 6),
k3=4 (т.к. в качестве третьей цифры можно взять любую цифру из 0, 2, 4, 6).
Согласно правила умножения, получаем ответ: N = k1k2k3= 6*7*4 = 168
Задачи для самостоятельного решения
1.10.Имеется 5 видов конвертов без марок и 4 вида марки. Сколькими способами можно выбрать конверт и марку для посылки письма?
1.20.При составлении одного варианта письменной контрольной работы по математике преподаватель располагает 4 задачами по геометрии, 8 – по алгебре и 3 – по тригонометрии. Сколькими способами можно составить этот вариант, если в него должно войти по одной задаче из перечисленных разделов?
1.30.Из двух полуфинальных групп, каждая их которых содержит по 6 команд, в финал выходит по одной команде. Сколько может быть различных вариантов участников финального матча?
1.40.В забеге участвуют 5 спортсменов. Сколькими способами могут распределиться места в результате забега?
1.50.В книге из 20 страниц на каких-либо трех страницах надо поместить по одно иллюстрации. Сколькими способами это можно сделать?
1.6.В первенстве края по футболу участвуют 11 команд. Сколько существует различных способов распределения мест в таблице розыгрыша, если на первое место могут претендовать только 4 определенные команды?
1.7.Имеется 9 белых, 12 красных и 11 синих шаров. Скольким способами можно разложить эти шары по двум урнам так, чтобы каждая урна содержала не менее четырех шаров каждого цвета?
P.S. Правило умножения не случайно называют основной формулой комбинаторики. С помощью правила умножения и правила сложения можно решить любую комбинаторную задачу. Для решения более сложных задач, сначала с помощью данных правил получают формулы комбинаторики, потом с помощью формул решают задачи.
|
Чтобы пройти в следующий круг соревнований, футбольной команде нужно набрать хотя бы 7 очков в двух играх. Если команда выигрывает, она получает 6 очков, в случае ничьей — 1 очко, если проигрывает — 0 очков. Найдите вероятность того, что команде удастся выйти в сле-дующий круг соревнований. Считайте в каждой игре вероятности выигрыша и проигрыша одинаковы и равны 0,3.


Задание. В классе 33 учащихся, среди них два друга – Андрей и Михаил. Учащихся случайным образом разбивают на 3 равные группы. Найдите вероятность того, что Андрей и Михаил окажутся в одной группе
Решение: Класс разбивается на 3 группы по 11 человек в группе. Андрей попадает в одну из групп, тогда вместе с ним в группе может оказаться еще 10 человек (в том числе и Михаил) из 32 оставшихся учащихся.
Всего исходов N = 32 Благоприятных исходов N(A) = 10
Вероятность равна P(A) = N(A)/N = 10/32 = 0,3125
Ответ: 0,3125
В некоторой местности наблюдения показали:
1. Если июньское утро ясное, то вероятность дождя в этот день 0,1.
2. Если июньское утро пасмурное, то вероятность дождя в течение дня равна 0,4.
3. Вероятность того, что утро в июне будет пасмурным, равна 0,3.
Найдите вероятность того, что в случайно взятый июньский день дождя не будет.
Решение:
Решением задачи будет вероятность суммы двух несовместных событий:
A: июньский день пасмурный (вероятность 0,3), но дождь не пошел (вероятность 1-0,4);
B: июньский день ясный (вероятность 0,7) и дождь не пошел (1-0,1).
Вероятности событий A и B равны:
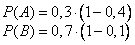 и вероятность их суммы и вероятность их суммы
 Ответ: 0,81. Ответ: 0,81.
Задача 4
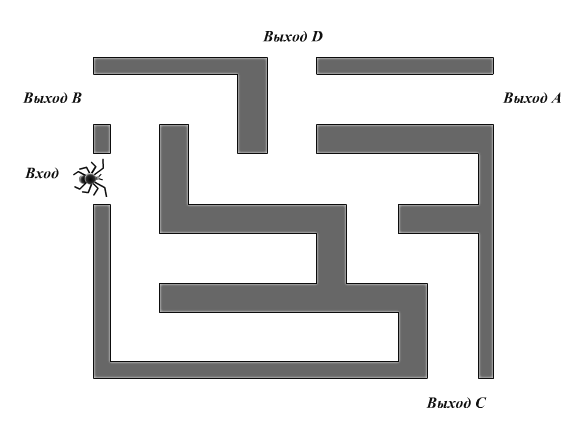
На рисунке изображён лабиринт. Паук заползает в лабиринт в точке "Вход". Развернуться и ползти назад паук не может, поэтому на каждом разветвлении паук выбирает один из путей, по которому ещё не полз. Считая, что выбор дальнейшего пути чисто случайный, определите, с какой вероятностью паук придёт к выходу D. Ответ: 0,0625


|
Уметь строить и исследовать простейшие математические модели (теория вероятностей)1.В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 8 очков. Результат округлите до сотых. Решение: Количество исходов, при которых в результате броска игральных костей выпадет 8 очков, равно 5: 2+6, 3+5, 4+4, 5+3, 6+2. Каждый из кубиков может выпасть шестью вариантами, поэтому общее число исходов равно 6·6 = 36. Следовательно, вероятность того, что в сумме выпадет 8 очков, равна 5: 36=0,138…=0,14
2.В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орел выпадет ровно один раз. Решeние: Равновозможны 4 исхода эксперимента: орел-орел, орел-решка, решка-орел, решка-решка. Орел выпадает ровно один раз в двух случаях: орел-решка и решка-орел. Поэтому вероятность того, что орел выпадет ровно 1 раз, равна 2 : 4= 0,5.
3.В чемпионате по гимнастике участвуют 20 спортсменок: 8 из России, 7 из США, остальные — из Китая. Порядок, в котором выступают гимнастки, определяется жребием. Найдите вероятность того, что спортсменка, выступающая первой, окажется из Китая. Решeние: В чемпионате принимает участие 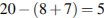 спортсменок из Китая. Тогда вероятность того, что спортсменка, выступающая первой, окажется из Китая, равна 5 : 20 = 0,25 спортсменок из Китая. Тогда вероятность того, что спортсменка, выступающая первой, окажется из Китая, равна 5 : 20 = 0,25
4.В среднем из 1000 садовых насосов, поступивших в продажу, 5 подтекают. Найдите вероятность того, что один случайно выбранный для контроля насос не подтекает. Решeние: В среднем из 1000 садовых насосов, поступивших в продажу, 1000 − 5 = 995 не подтекают. Значит, вероятность того, что один случайно выбранный для контроля насос не подтекает, равна 995 : 1000 =0,995
5.Фабрика выпускает сумки. В среднем на 100 качественных сумок приходится восемь сумок со скрытыми дефектами. Найдите вероятность того, что купленная сумка окажется качественной. Результат округлите до сотых. Решeние: По условию на каждые 100 + 8 = 108 сумок приходится 100 качественных сумок. Значит, вероятность того, что купленная сумка окажется качественной, равна 100: 108 =0,925925…= 0,93
6.В соревнованиях по толканию ядра участвуют 4 спортсмена из Финляндии, 7 спортсменов из Дании, 9 спортсменов из Швеции и 5 — из Норвегии. Порядок, в котором выступают спортсмены, определяется жребием. Найдите вероятность того, что спортсмен, выступающий последним, окажется из Швеции. Решeние: Всего в соревнованиях принимает участие 4 + 7 + 9 + 5 = 25 спортсменов. Значит, вероятность того, что спортсмен, который выступает последним, окажется из Швеции, равна 9 : 25 =0,36
7.Научная конференция проводится в 5 дней. Всего запланировано 75 докладов — первые три дня по 17 докладов, остальные распределены поровну между четвертым и пятым днями. Порядок докладов определяется жеребьёвкой. Какова вероятность, что доклад профессора М. окажется запланированным на последний день конференции? Решeние: За первые три дня будет прочитан 51 доклад, на последние два дня планируется 24 доклада. Поэтому на последний день запланировано 12 докладов. Значит, вероятность того, что доклад профессора М. окажется запланированным на последний день конференции, равна 12 : 75 =0,16
8.Конкурс исполнителей проводится в 5 дней. Всего заявлено 80 выступлений — по одному от каждой страны. В первый день 8 выступлений, остальные распределены поровну между оставшимися днями. Порядок выступлений определяется жеребьёвкой. Какова вероятность, что выступление представителя России состоится в третий день конкурса? Решeние: На третий день запланировано 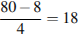 выступлений. Значит, вероятность того, что выступление представителя из России окажется запланированным на третий день конкурса, равна 18 : 80 =0,225 выступлений. Значит, вероятность того, что выступление представителя из России окажется запланированным на третий день конкурса, равна 18 : 80 =0,225
9.На семинар приехали 3 ученых из Норвегии, 3 из России и 4 из Испании. Порядок докладов определяется жеребьёвкой. Найдите вероятность того, что восьмым окажется доклад ученого из России. Решeние: Всего в семинаре принимает участие 3 + 3 + 4 = 10 ученых, значит, вероятность того, что ученый, который выступает восьмым, окажется из России, равна 3:10 = 0,3.
10.Перед началом первого тура чемпионата по бадминтону участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 26 бадминтонистов, среди которых 10 участников из России, в том числе Руслан Орлов. Найдите вероятность того, что в первом туре Руслан Орлов будет играть с каким-либо бадминтонистом из России? Решeние: В первом туре Руслан Орлов может сыграть с 26 − 1 = 25 бадминтонистами, из которых 10 − 1 = 9 из России. Значит, вероятность того, что в первом туре Руслан Орлов будет играть с каким-либо бадминтонистом из России, равна 9 : 25 = 0,36
11.В сборнике билетов по биологии всего 55 билетов, в 11 из них встречается вопрос по ботанике. Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику достанется вопрос по ботанике. Решение: 11 : 55 = 0,2
12.На чемпионате по прыжкам в воду выступают 25 спортсменов, среди них 8 прыгунов из России и 9 прыгунов из Парагвая. Порядок выступлений определяется жеребьёвкой. Найдите вероятность того, что шестым будет выступать прыгун из Парагвая.
13.Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика выпускает 30% этих стекол, вторая — 70%. Первая фабрика выпускает 3% бракованных стекол, а вторая — 4%. Найдите вероятность того, что случайно купленное в магазине стекло, окажется бракованным. Решение. Переводим %% в дроби. Событие А - "Куплены стекла первой фабрики". Р(А)=0,3
Событие В - "Куплены стекла второй фабрики". Р(В)=0,7 Событие Х - " Стекла бракованные".
Р(А и Х) = 0.3*0.03=0.009 Р(В и Х) = 0.7*0.04=0.028 По формуле полной вероятности:Р = 0.009+0.028 = 0.037
14.Если гроссмейстер А. играет белыми, то он выигрывает у гроссмейстера Б. с вероятностью 0,52. Если А. играет черными, то А. выигрывает у Б. с вероятностью 0,3. Гроссмейстеры А. и Б. играют две партии, причем во второй партии меняют цвет фигур. Найдите вероятность того, что А. выиграет оба раза. Решение: 0,52 * 0,3 = 0,156.
15.Вася, Петя, Коля и Лёша бросили жребий — кому начинать игру. Найдите вероятность того, что начинать игру должен будет Петя.
Решение: Случайный эксперимент — бросание жребия.
В этом эксперименте элементарным событием является участник, который выиграл жребий.
Перечислим возможные элементарные события:
(Вася), (Петя), (Коля), (Лёша).
Их будет будет 4, т.е. N=4. Жребий подразумевает, что все элементарные события равновозможны.
Событию A= {жребий выиграл Петя} благоприятствует только одно элементарное событие (Петя). Поэтому N(A)=1.
Тогда P(A)=0,25 Ответ: 0,25.
16.В чемпионате мира участвуют 16 команд. С помощью жребия их нужно разделить на четыре группы по четыре команды в каждой. В ящике вперемешку лежат карточки с номерами групп: 1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 3, 4, 4, 4, 4. Капитаны команд тянут по одной карточке. Какова вероятность того, что команда России окажется во второй группе? Решение: Всего исходов -16.Из них благоприятных, т.е. с номером 2, будет 4. Значит, 4 : 16=0,25
17.На экзамене по геометрии школьнику достаётся один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос на тему «Вписанная окружность», равна 0,2. Вероятность того, что это вопрос на тему «Параллелограмм», равна 0,15. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем. 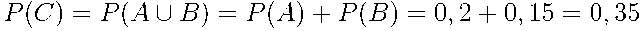 . .
18.В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,3. Вероятность того, что кофе закончится в обоих автоматах, равна 0,12. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.
Определим события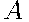 = {кофе закончится в первом автомате}, = {кофе закончится в первом автомате}, 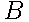 = {кофе закончится во втором автомате}. = {кофе закончится во втором автомате}.
По условию задачи 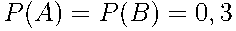 и и 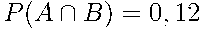 . .
По формуле сложения вероятностей найдем вероятность события
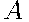 и и 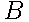 = {кофе закончится хотя бы в одном из автоматов}: = {кофе закончится хотя бы в одном из автоматов}:
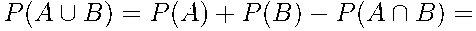
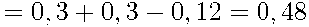 . .
Следовательно, вероятность противоположного события {кофе останется в обоих автоматах} равна
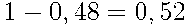 . . |
 Скачать 3.05 Mb.
Скачать 3.05 Mb.














