Теория вероятности. Вероятность независимых событий А и В равны соответственно 2. Задача. Монету бросают четыре раза. Найдите вероятность того, что орел выпадет ровно три раза
 Скачать 26.15 Kb. Скачать 26.15 Kb.
|
|
Вероятность независимых событий А и В равны соответственно 2/3 и 1/2. В результате испытания произошло ровно одно из них. Найдите вероятность того, что это было событие А. Условная вероятность - формула Байеса Р ( А | 1 ) = Р (1 | А ) * Р (А ) / Р (1) Р ( 1 | А ) = Р ( не В ) = 1/2 Р (1) = Р ( А ) * Р ( не В ) + Р (В ) * Р ( не А ) = 2/3 * 1/2 + 1/2 * 1/3 = 1 / 2 Р ( А | 1 ) = 1/2 * 2/3 / ( 1/2 ) = 2/3 В этой задаче оказалось совпадение с вероятностью Р ( А ) . Это именно совпадение. Найдем также вероятность Р ( В | 1 ) чтобы убедится что сумма Р ( А | 1 ) + Р ( В | 1 ) = 1 Р ( В | 1 ) = Р (1 | В ) * Р ( В ) / Р ( 1 ) = Р ( не А ) * Р (В ) / Р ( 1 ) = 1/3 * 1/2 / ( 1/2 ) = 1/3 Проверка верна ! Вероятность независимых событий А и Б равны соответственно 4/5 и 1/2.В результате испытания произошло ровно одно из них. Вероятность независимых событий А и Б равны соответственно 4/5 и 1/2.В результате испытания произошло ровно одно из них. Найдите вероятность того, что это было событие А Кто знает как решать, подскажите пожалуйста, интересует само решение. Правильный ответ 4/5 Дополнен 9 лет назад Вероятность независимых событий А и Б равны соответственно 2/3 и 1/3.В результате испытания произошло ровно одно из них. Найдите вероятность того, что это было событие А аналогичное задание, но у меня не сходится с ответами P(h1)=2/3 P(h2)=1/3 P(a/h1)=1/3 P(a/h2)=2/3 2/3*1/3+1/3*2/3=4/9 2/3*1/3 / 4/9 =1/2 а варианты ответов 4/9, 2/3, 1/5, 4/5 где я ошибаюсь? По формуле полной вероятности: P(A)=0.8•0.5+0.2•0.5=0.5 По формуле Бейеса: P(H₁|A)=0.8•0.5/0.5=0.8=4/5 Задача. Монету бросают четыре раза. Найдите вероятность того, что орел выпадет ровно три раза. По условию задачи, всего бросков было n = 4. Требуемое число орлов: k = 3. Подставляем n и k в формулу: 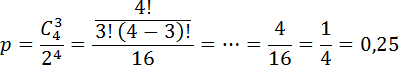 С тем же успехом можно считать число решек: k = 4 − 3 = 1. Ответ будет таким же Вероятность сдать тест для Андрея равна 1/2 для бориса 3/7.Тест сдал один из них. Тогда вероятность того что это был - Андрей, равна ...3/7; 7/13; 2/7; 4/7 1/2 * 4/7+1/2*3/7=1/2 вероятность что сдал один из них 1/2*4/7=2/7 вероятность что сдал сдал один из них, а именно Андрей 2/7 : 1/2= 4/7 искомая вероятность если тест сдал один из них, а именно Андрей. То есть Андрей сдал тест. Вероятность этого 1/2. То второй чел тест не сдал. То есть Борис не сдал. Вероятность этого 4/7. Вероятность того, что эти события произойдут одновременно, равна произведению вероятностей (ибо события не зависят друг от друга): 1/2 * 4/7 = 2/7 Вероятность сдать тест для Андрея равна 3/7, для Бориса – 1/3.Тест сдал один из них. Найдите вероятность того, что это был Андрей Ответ: 2/5; 2/7; 9/16(Неправильно); 3/5 3/7*2/3+3/7*1/3=2/7 Вероятность сдать тест для Андрея равна 1/3, для Бориса – 3/10.Тест сдал один из них. Найдите вероятность того, что это был Борис Ответ: 9/19(Неправильно); 1/5; 7/13; 6/13 1/3*4/10+1/3*3/10= Вероятность сдать тест для Андрея 3/5, а для Бориса 1/5. Тест сдал один из них. Найдите вероятность того, что это был Борис. Событие А0-Борис сдал А1-Борис не сдал Вероятности обоих равны 1/2 Событие В- сдал только один. Тогда Р(В/А0)-вероятность того, что сдал только 1 при условии, что Борис сдал-это вероятность того, что Андрей не сдал =2/5(1-3/5) А Р(В/А1)-вероятность того, что сдал только 1 при условии , что Борис не сдал- это вероятность того, что Андрей сдал =3/5. По ф-ле Байерса Р(А0/В)=Р(В/А0)*Р(А0)/(Р(В/А0)*Р(А0)+Р(В/А1)*Р(А1))=(2/5*1/2):((2/5*1/2)+(3/5*1/2))=2/10:5/10=2/5 Вероятность сдать тест для Андрея равна 1/3, для Бориса – 3/10.Тест сдал один из них. Найдите вероятность того, что это был Борис А не сдал 1/3(1-1/3)=2/9 (1/3*1/2)/((1/3*1/2)+(1/3*1/2))=1/2 Случайная величина ξ распределена равномерно на отрезке [-1;3]. Дополнен 12 лет назад Найти ее дисперсию и вероятность попадания ξ в интервал [1/2;1/2]. Для равномерного распределения М (ξ)=(a+b)/2=(-1+3)/2=1; D(ξ)=(b-a)²/12=(3+1)²/12=16/12=4/3. P(-½≤ξ≤½)=[от -½ до ½] ∫(1/(b-a)dξ=(1/4)•[от -½ до ½] ∫dξ= =(1/4)•ξ[от -½ до ½] =(1/4)•(½+½)=0,25. Случайная величина ξ нормально распределена на отрезке [-7; 2]. Найдите М(ξ) и D(ξ). М (ξ)=(a+b)/2=(-7+2)/2=-2.5 D(ξ)=(b-a)²/12=(2+7)^2/12=6.75 Дискретная случайная величина задана законом распределения вероятностей:  Тогда её математическое ожидание равно 2,1 если … Ответы: a = 0,2; b = 0,7 a = 0,4; b = 0,5 a = 0,7; b = 0,2 a = 0,35; b = 0,65 |
