Методы принятия управленческих решений. контрольная Методы принятия управленческих решений. Теоретическая часть 3 Практическая часть 11

• Название: Теоретическая часть 3 Практическая часть 11
• Анкор: Методы принятия управленческих решений
• Дата: 20.09.2022
• Размер: 91.94 Kb.
• Имя файла: контрольная Методы принятия управленческих решений.docx
• Тип: Документы; #686791

Содержание

Теоретическая часть 3

Практическая часть 11

Список использованных источников 18

Теоретическая часть

Классической формой оценки экономической эффективности решения является сопоставление затрат и результатов в стоимостном выражении. Оно является основой оценки альтернативных действий при выборе экономических решений. Так, например, при планировании, требуется учитывать большое число критериев. Ограничиваться оценкой экономической эффективности невозможно, так как при этом не учитываются качественные факторы, практически не поддающиеся количественным оценкам, а также наличие рисков. Поэтому все шире применяются методы оценок, сочетающие точные расчеты с субъективной оценкой качественных критериев (отношения трудового коллектива к проблеме, авторитет руководителя.). Именно таким образом взвешиваются преимущества различных действий, и делается выбор оптимального варианта. Инструментами качественной оценки являются установление приоритетов, ранги, оценка в баллах и др.

Распространенным методом сравнения вариантов решений являются оценочные баллы. Сущность его состоит:

1. в установлении на субъективной основе коэффициента значимости (веса) каждого из принятых критериев оценки эффективности (Vj),

2. определении каждого из результатов во взаимосвязи с коэффициентом значимости (весом) - Еij Vj,

3. суммировании результатов по каждому критерию имеющихся вариантов (альтернатив) - У Еij Vj.

Пример. Разработаны три варианта капиталовложений - В1, В2, В3, которые оцениваются по шести критериям - K1, K2, K3, К4, K5, K6.

По результатам сопоставления выбирается тот вариант, общая сумма эффективности по которому составляет наибольшее значение

Линия поведения руководителя при выборе решений зависит и от знания им возможности возникновения объективных условий. Поэтому руководитель предварительно должен ставить перед собой вопросы:

1. Какие объективные условия могут повлиять на результаты альтернативных решений и можно ли учесть (предвидеть) их возникновение?

2. Можно ли установить частоту возникновения объективных условий и насколько она постоянна?

Учитывая возникновение объективных условий и определив варианты решений, можно рассчитать и ожидаемые результаты по каждому их сочетанию, а на этой основе - степень соответствия поставленным целям. Для удобства анализа ожидаемых результатов решений при разных объективных условиях используется матрица решений. Так, обозначим объективные условия через уj, где j принимает значение от 1 до т; варианты решений

- через Rj, где j - количество вариантов; ожидаемый результат при каждом сочетании объективных условий и вариантов решения - через Оij. Построим матрицу решений, которая при т = 3, j =4 примет вид:

Указанная матрица решений признана универсальной и может применяться для решения самых различных производственных задач. При этом объективные условия (Уj) характеризуют неуправляемые факторы, которые могут весьма существенно влиять на результаты решений. Результаты (Оij) отражают то, что будет достигнуто при выборе конкретного варианта и возникновении определенных объективных условий.

Следует заметить, что составление матрицы решений требует глубоких знаний специфики производства ЛПР, творческого мышления, опыта для достоверного прогнозирования появления возможных ситуаций (объективных условий) и их потенциального влияния на результаты деятельности. Приведенная матрица решений может быть использована для выбора решений и в условиях риска.

Чем сложнее проблема, тем ответственнее выбор решения. Поэтому данный этап предполагает сопоставление ожидаемого экономического и социального эффекта по разработанным альтернативам. Учитывается и воздействие внешней среды, в частности, влияние неуправляемых факторов на результаты принятого решения, оценивается степень возможного риска. Действие фактора неопределенности при принятии решения связывается с уровнем управления и длительностью периода реализации решений. Чем выше уровень управления и продолжительнее временной период, тем больше факторов являются управляемыми.

Реализация решения может привести к результатам, не отвечающим поставленной цели. Поэтому на данном этапе выделяются альтернативы, непосредственно связанные с достижением цели и удовлетворяющие определенным ограничениям. В качестве критерия оценки решения может выступать эффективность, фактор времени; ограничением - степень риска.

Существуют и другие способы определения наилучшего варианта решений. Доусоном рекомендуется, в зависимости от ситуации, руководствоваться одним из пяти правил игры:

1. 
   не бросаться от варианта к варианту, а определить время обдумывания каждого, последовательно рассмотреть их положительные и отрицательные стороны;
   
2. 
   определить линию поведения, особенно по принципиальным вопросам: соотносится ли принимаемое решение с вашей жизненной позицией, жизненными ценностями. Если нет единства, то возможна корректировка собственных взглядов;
   
3. 
   глубоко анализировать сложившуюся ситуацию для определения объективности суждений;
   
4. 
   при наличии значительного количества вариантов (более двух - трех) следует руководствоваться принципом здравого смысла. Облегчает выбор в этой ситуации опора на логические суждения;
   
5. 
   - в поисках решения новых проблем целесообразно проявлять творчество, инициативное отношение, которое часто завершается успехом.
   

При появлении проблемы необходимо отнести ее к одному из правил игры:

1. 
   не бросаться из стороны в сторону;
   
2. 
   определить линию поведения;
   
3. 
   глубоко анализировать ситуацию;
   
4. 
   руководствоваться здравым смыслом;
   
5. 
   проявлять творчество.
   

В процессе подготовки и выбора решения необходимо учитывать две стороны: формализованную и поведенческую. Первая - нормативная, обусловлена математизацией процесса выработки решения, вторая - особенностями поведения лиц, принимающих управленческое решение в конкретной обстановке. Это обстоятельство объясняется тем, что последнее слово в выборе окончательного решения принадлежит не «математике» и не машине, а человеку, зависит от его индивидуальных особенностей: профессионализма, склонности к риску и др. Кроме того, по соображениям конъюнктуры рынка и другим может приниматься решение и не лучшее с точки зрения проведенных расчетов. В связи с этим в рамках математической теории принятия решений выделяются нормативные модели (о чем уже упоминалось), ориентированные на расчет альтернатив и выбор оптимального варианта в условиях установленных критериев и ограничений. Исходя из данного подхода, нормативные модели «расписывают», как ЛПР должно принимать решение. В этом случае абстрагируются от личностных особенностей, поведение ЛПР с «позиции здравого смысла» принимается как аксиома.

С учетом влияния «человеческого фактора» в теории принятия решений выделяются дескриптивные модели, поведенческий аспект руководителя в которых является определяющим. В них раскрываются процессы и силы, объясняющие стратегию и тактику, применяемую ЛПР при разработке, либо их полное отсутствие.

Разработка дескриптивных моделей, построенных на прогнозах поведения ЛПР, достаточно сложная задача, требующая учета психологических аспектов наряду с используемыми логическими аргументами (например, ценностных ориентации, характера мышления, темперамента, способностей, волевого и эмоционального уровней). Логическая схема процесса подготовки и реализации решений предполагает комплексное использование разработанных нормативных и дескриптивных моделей.

Субъективный фактор, а именно особенности восприятия и интерпретации процесса принятия решений, лежит в основе выделения следующих моделей принятия решений: рациональной, ограниченно рациональной (личностно-ограниченной рациональности и организационно-ограниченной рациональности) и политической.

Рациональная модель строго ориентирована на получение максимальной выгоды организации при тщательном поиске альтернатив и выборе наилучшей (оптимальной).

Модель ограниченной рациональности имеет две разновидности, в зависимости от присутствия и преобладания у менеджера, принимающего решение, определенных свойств: ограниченности знаний, представлений или приверженности привычкам, предубеждениям. В этом случае, как правило, цель максимизации заменяется удовлетворенностью решением: неплох результат и минимальны затраты на его достижение. Поиском оптимального решения менеджеры не озабочены.

Политическую модель решений характеризует обусловленность их индивидуальными интересами лиц, принимающих решение. Данная модель решения имеет классически бюрократическую окраску и по существу является функцией распределения власти в организации.

3. Анализ альтернатив при разработке групповых решений

Коллективное творчество при разработке и выборе решений имеет ряд преимуществ:

1. 
   уменьшается вероятность ошибок, так как участвующие лица могут оперативно поправить друг друга; усиливается интерес к проблеме и работе в целом;
   
2. 
   повышается степень доверительности в межличностных отношениях;
   
3. 
   улучшается обоснованность принимаемых решений за счет использования, как правило, проверенной информации, которая становится более полной, а предложения - более четкими.
   

Сложные задачи, лишенные определенности, то есть достаточной информации для их решения, тем не менее, решаются, и нередко групповым методом. Однако мнения участников процесса разработки решения могут не совпасть. Как в этом случае выбрать вариант решения? В подобной ситуации используется ряд стратегий выработки группового решения. Среди них самая простая - стратегия простого большинства голосов. Например, на научно-производственных совещаниях принимается решение, соответствующее предпочтениям большинства членов группы. Метод прост, но не лишен погрешностей, так как не учитывается мнение меньшинства, в котором могут содержаться рациональные идеи, и кроме того, мотивы принятого решения у разных членов группы могут быть различны.

Другим методом выбора группового решения является стратегия суммирования рангов. Сущность метода рассмотрим на примере. Представим, что решения принимаются группой из трех человек и разработаны четыре альтернативных варианта решения проблемы (b1,..b4). Какую из альтернатив принять? Методика выхода из данной ситуации включает такие действия:

1. Каждый из участников ранжирует имеющиеся альтернативы с 1 (высший ранг) до 4.

2. По каждой альтернативе определяется сумма рангов.

3. Выбирается вариант, сумма рангов у которого наименьшая.

В табличной форме выбор решения методом суммирования рангов выглядит следующим образом:

Сумма рангов по:

bз =1+2+4=7

b2 =1+2+3=6

B1 =1+3+4=8

b4 =2+3+4=9

Следовательно, из разработанных альтернатив второй вариант (b2) будет использован для практического внедрения как набравший наименьшую сумму рангов (имея в виду, что 1 - означает выбор альтернативы в первую очередь).

Существует и так называемое компьютерное обсуждение. Суть его состоит в передаче от одной ЭВМ к другой необходимой информации. При этом она корректируется с учетом полезности предыдущего адресата и с соблюдением анонимности передается следующему. Лица, участвующие в оценках (респонденты), могут быть неизвестны друг другу. Такой вариант выбора решения состоит из пяти стадий: исследование, интерпретация, примирение, оценка, подведение итогов.

На первой стадии пользователям ЭВМ предлагается подключиться к коллективному обсуждению. Далее в компьютерную сеть вводится информация-предложение (например, об открытии кафе, изменении ассортимента в магазине и т.д.). Предлагается указать по три положительных и отрицательных довода относительно высказанной идеи.

На второй стадии специалисты анализируют мнения пользователей по поводу предложения.

На третьей стадии исключаются крайне резкие ответы (безоговорочно принимающие или отвергающие) и делается попытка «примирения» оставшихся респондентов путем выяснения у них отношения к предлагаемым альтернативам решения задачи. Например, в связи с изменением ассортимента ставятся вопросы типа «Как вы отнесетесь к тому, если... (часы торговли конкретными товарами будут в пределах трех часов утром или вечером? Относительно оказания дополнительных услуг и др.).

На четвертой стадии оцениваются все имеющиеся предложения и на этой основе составляется предварительный отчет.

На пятой стадии информация с убедительной аргументацией выбранного решения вновь направляется пользователям ЭВМ. Благодаря развернутой информации появляется возможность изменить мнение тех, кто отвергал первоначальное предложение и утвердиться во мнении лицам с положительным отношением к рассматриваемому вопросу. Преимущества компьютерного варианта принятия коллективного решения состоят в том, что:

1. 
   увеличивается число вовлеченных в процесс выработки решения;
   
2. 
   работа по принятию решения обходится дешевле, чем в условиях, когда оно принимается сообща явочным путем, легче снимаются противоречия во мнениях за счет анонимности лиц, обсуждающих проблему;
   
3. 
   исключается возможность влияния на решения управленческих работников предприятия.
   

Численность группы разработчиков совместных (коллегиальных) решений зависит от их типа. Для предварительного обсуждения (осмысления) конкретных проблем целесообразно небольшое количество участников; для проблем перспективного значения число участвующих увеличивается. Однако при значительном количестве людей труднее принять решение, возрастает количество человеко-часов, в том числе на организацию этих мероприятий. Если в обсуждении принимают участие более восьми человек, возможно формирование группировок, осложняющих выбор решения.

В технологии разработки управленческих решений и организации их исполнения важное место отводится сетевому моделированию.

Практическая часть

Задача 1

AB	250	450	300
300	2	1	6
400	1	3	5
300	5	2	4

Здесь А = (300, 400, 300) - вектор запасов поставщиков (склады №1, №2, №3), В = (250, 450, 300) - вектор запросов потребителей (магазины №1, №2, №3).



= 300 + 400 + 300 = 1000;



= 250 + 450 + 300 = 1000.

Так как = , то имеем задачу с правильным балансом.

Находим начальное опорное решение методом северо-западного угла (табл. 1).

Таблица 1. Начальное опорное решение

AB	250	450	300
300	2 250	1 50	6 -3
400	1 +3	3 400	5 0
300	5 -2	2 0	4 300

Значение целевой функции на данном опорном решении:

Z(X) = 250·2 + 50·1 + 400·3 + 0·2 + 400·4 = 2950.

Решаем задачу методом потенциалов.

Для проверки оптимальности опорного решения находим потенциалы. Записываем систему уравнений для нахождения потенциалов.

u1 + v1 = 2,

u2 + v1 = 1,

u2 + v2 = 3,

u3 + v2 = 2,

u3 + v3 = 4.

Система состоит из 5 уравнений и имеет 6 неизвестных. Система неопределенная. Одному из потенциалов задаем значение произвольно: пусть u1 = 0. Находим остальные потенциалы:

u2 = 2; u3 = 1;

v1 = 2; v2 = 1; v3 = 3.

Проверяем опорное решение на оптимальность. Для этого вычисляем оценки Дij для всех незаполненных клеток таблицы:

Д12 = u1 + v2 - c12 = 0 - 3 - 3 = -6;

Д13 = u1 + v3 - c13 = 0 - 4 - 2 = -6;

Д23 = u2 + v3 - c23 = 4 - 4 - 4 = -4;

Д31 = u3 + v1 - c31 = 5 + 1 - 4 = 2.

Полученное опорное решение не является оптимальным, т.к. имеются положительные оценки.

Переходим к новому опорному решению. Для клетки (3, 1) строим цикл (табл. 1). Осуществляем сдвиг по циклу на величину и = 150. Получаем новое опорное решение (табл. 2).

Таблица 2. Новое опорное решение

AB	250	250	100
100	1 100	3 -4	2 -4
200	5 -2	1 200	4 -4
300	4 150	2 50	1 100

Значение целевой функции на данном опорном решении:

Z(X) = 100·1 + 200·1 + 150·4 + 50·2 + 100·1 = 1100.

Для проверки оптимальности опорного решения находим потенциалы. Записываем систему уравнений для нахождения потенциалов.

u1 + v1 = 1,

u2 + v2 = 1,

u3 + v1 = 4,

u3 + v2 = 2,

u3 + v3 = 1.

Система состоит из 5 уравнений и имеет 6 неизвестных. Система неопределенная. Одному из потенциалов задаем значение произвольно: пусть u1 = 0. Находим остальные потенциалы:

u2 = 2; u3 = 3;

v1 = 1; v2 = -1; v3 = -2.

Проверяем опорное решение на оптимальность. Для этого вычисляем оценки Дij для всех незаполненных клеток таблицы:

Д12 = u1 + v2 - c12 = 0 - 1 - 3 = -4;

Д13 = u1 + v3 - c13 = 0 - 2 - 2 = -4;

Д21 = u2 + v1 - c21 = 2 + 1 - 5 = -2;

Д23 = u2 + v3 - c23 = 2 - 2 - 4 = -4.

Полученное опорное решение является оптимальным, т.к. все оценки отрицательные.

Ответ: Наименьшие затраты на перевозку составят minZ = 1100 условных денежных единиц при оптимальном плане перевозок

X* = .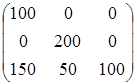


Задача №2 (модель Леонтьева)

Даны вектор непроизводственного потребления C и матрица межотраслевого баланса А: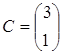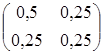

 

, А = .

Найти вектор валового выпуска, обеспечивающий данный вектор потребления.

Решение: Из равенства C = X - AX следует, что X = (E - A)-1C.

Находим матрицу (Е - А):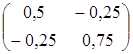



(Е - А) = - = .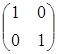



Находим определитель матрицы |Е - А|: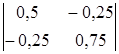



|Е - А| = = = 0,3125.

Определитель не равен нулю, матрица (Е - А) невырожденная и имеет обратную.

Транспонируем матрицу (Е - А):

(Е - А)Т =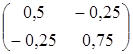



и находим присоединенную к ней матрицу: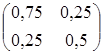



(Е - А)* = .

Находим обратную матрицу (Е - А)-1: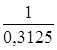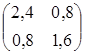



(Е - А)-1 = = · = .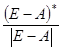



Элементы матрицы (Е - А)-1 неотрицательные. Следовательно, исходная матрица межотраслевого баланса A продуктивна.

Определяем вектор валового выпуска X = (E - A)-1C:

Х = = = .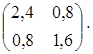



Ответ: .

Задача №3 (модель Неймана)

Даны матрицы A, B технологических процессов, вектор цен P и вектор начальных запасов S: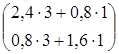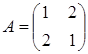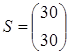



Найти интенсивности технологических процессов, максимизирующих стоимость выпуска продукции за один производственный цикл и максимальную стоимость.

Решение:

Пусть - вектор-матрица искомых интенсивностей. Тогда для их нахождения составим задачу линейного программирования: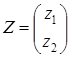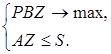



Находим:

PBZ > max > max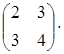



> max 22z1 +30z2 > max.

AZ ? S ? ? ?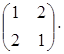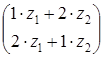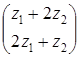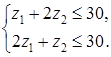



Записываем задачу линейного программирования в развернутой форме: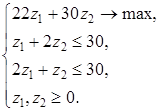



Решаем задачу линейного программирования графическим методом.

Находим область допустимых решений задачи и строим график как показано на рисунке:

(1) x1 + 2x2 = 30,

(x1 = 0, x2 = 15),

(x1 = 30, x2 = 0).

(2) 2x1 + x2 = 30,

(x1 = 0, x2 = 30),

(x1 = 15, x2 = 0).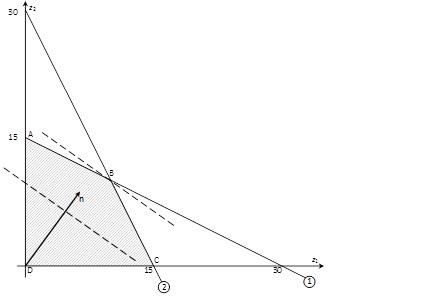



Область допустимых решений ограничена многоугольником ABCD, который показан на рисунке. На этом же рисунке строим нормаль линий уровня = (22, 30) и одну из линий уровня, имеющую общие точки с областью допустимых решений.

Для нахождения максимума целевой функции линию уровня перемещаем в направлении нормали до опорной прямой. Эта прямая проходит через точку B, лежащую на пересечении прямых (1) и (2). Решая систему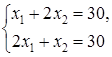



получаем точку максимума Z* = (10, 10). Максимальная стоимость продукции, выпущенной за один цикл составит Zmax = 22·10 + 30·10 = 520 ден. ед.

Ответ: 520 ден. ед.

Список использованных источников

1. 
   Геращенкова Т.М., Маркелова О.О. Методы принятия управленческих решений. Учебное пособие для проведения практических занятий и самостоятельной работы. - Брянск: Издательство Брянской ГСХА, 2018. - 72 с.
   
2. 
   Грибов П.Г., Тищенко Т.А., Бардина Н.Ю. Методы принятий управленческих решений. - М.: МИИР, 2016. - 196 с.
   
3. 
   Кирильчук С.П., Шевченко Е.В. Методы принятия управленческих решений в экономике. - Симферополь: Ариал, 2020. - 102 с.
   
4. 
   Сорокин А.В., Жарикова А.В. Методы принятия управленческих решений. - Рубцовск: Рубцовский индустриальный институт, 2015. - 54 с.
   
5. 
   Яресь О.Б. Методы принятия управленческих решений. Владимир: Владимирский государственный университет, 2018. – 66 с.