Теоретическая часть Две матрицыАиВ называются равными, если

• Название: Теоретическая часть Две матрицыАиВ называются равными, если
• Дата: 12.01.2022
• Размер: 0.82 Mb.
• Имя файла: Matem_1kurs_1_sem_Gazizov_E_R (2).doc
• Тип: Документы; #329096
• страница: 2 из 2

Практическая часть
1. Если и , то матрица А – В имеет вид

1)

2)

+3)

4)

2. Если и , то матрица В – А имеет вид

1)

2)

3)

+4)

3. Если и , то матрица А – В имеет вид

1)

+2)

3)

4)

4. Если и , то матрица А^Т+ В имеет вид

1)

2)

+3)

4)

5. Если и , то матрица В^Т+ А имеет вид

+1)

2)

3)

4)

6. Дана матрица 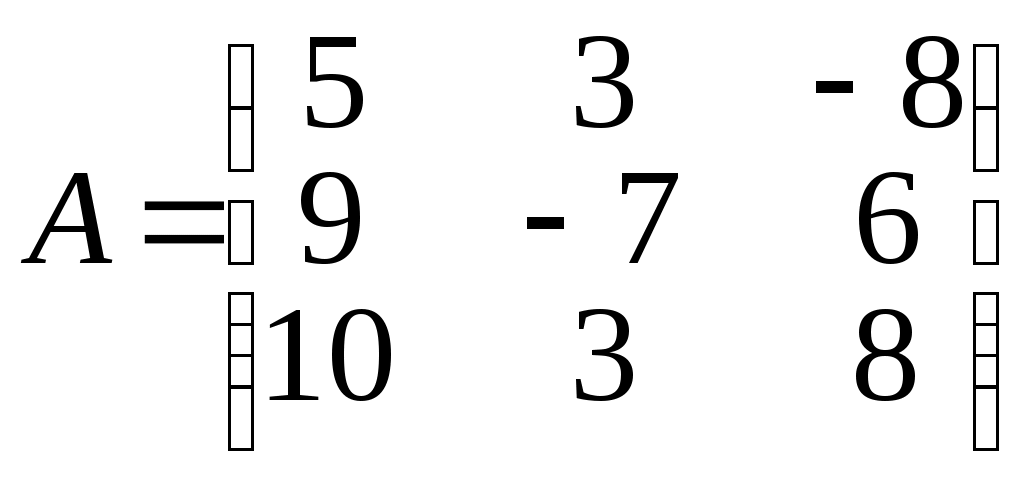, тогда сумма элементов этой матрицы, равна

1) 6

2) 11

3) –4

+4) 9

7. Дана матрица 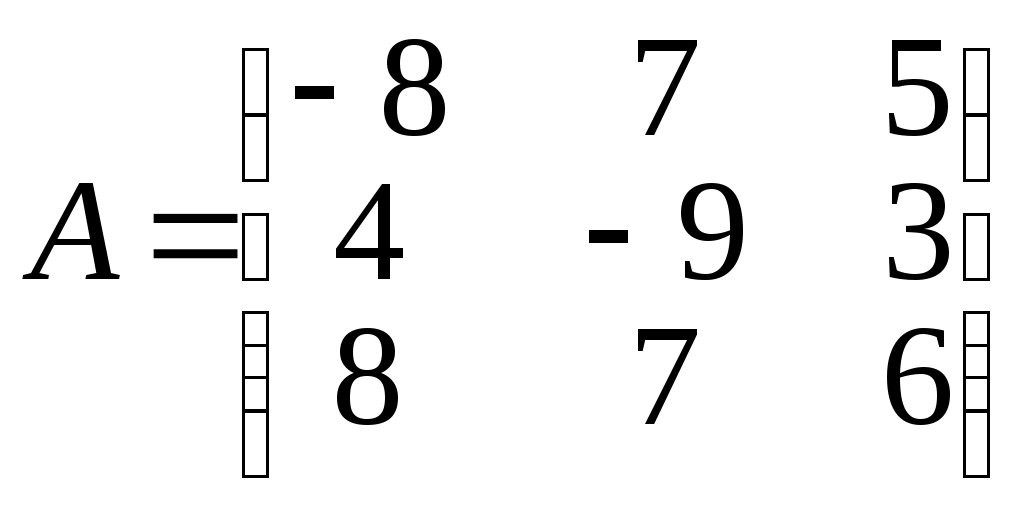, тогда сумма элементов

этой матрицы, равна

1) 3

+2) 18

3) –4

4) 22

8. Дана матрица 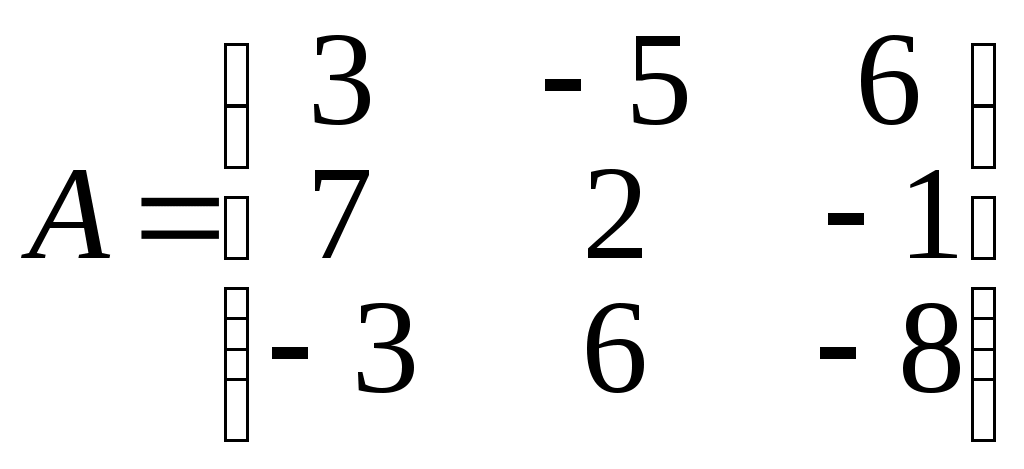, тогда сумма элементов

этой матрицы, равна

1) –3

2) 5

+3) 16

4) 11

9. Матрица не имеет обратной при λ равном

1) 1

2) –3

3) 2

+4) –1

10. Матрица не имеет обратной при λ равном

1) 1

+2) –2

3) 2

4) 4

11. Матрица не имеет обратной при λ равном

1) –4

2) 2

+3) –3

4) 3

12. Матрица не имеет обратной при λ равном

1) 2

2) –6

3) 5

+4) –5

13. Матрица не имеет обратной при λ равном

+1) –2

2) 2

3) –5

4) 5

14. Матрица не имеет обратной при λ равном

1) 2

+2) –1

3) –2

4) 5

15. Определитель после вычисления равен

+1) 22

2) –22

3) –2

4) 2

16. Определитель после вычисления равен

1) 13

+2) –13

3) –5

4) 5

17. Определитель при β равном

1) –4

+2) 1

3) 0

4) 2

18. Определитель при β равном

1) –2

2) 6

3) 0

+4) 2

19. Определитель при β равном

1) –2

2) –1

+3) 1

4) 0

20. Определитель при β равном

+1) 2

2) 0

3) –6

4) 1

21. Определитель при β равном

1) 3

2) –8

+3) 1

4) 0

22. Если (x₀, y₀) – решение системы линейных уравнений



тогда x₀ – y₀ равно

1) –1

2) 3

3) 1

+4) –3

23. Если (x₀, y₀) – решение системы линейных уравнений



тогда x₀ + y₀ равно

+1) –3

2) 3

3) 1

4) –1

24. Если (x₀, y₀) – решение системы линейных уравнений



тогда y₀ – x₀ равно

1) 4

+2) –4

3) 2

4) –2

25. Если (x₀, y₀) – решение системы линейных уравнений



тогда x₀ – y₀ равно

1) –2

2) 4

+3) 2

4) –4

26. Если (x₀, y₀) – решение системы линейных уравнений



тогда x₀ + y₀ равно

1) 5

2) –5

3) –1

+4) 1

27. Если (x₀, y₀) – решение системы линейных уравнений



тогда y₀ – x₀ равно

1) –3

2) 3

+3) 1

4) –1

28. Если (x₀, y₀) – решение системы линейных уравнений



тогда x₀ – y₀ равно

+1) 5

2) –5

3) 1

4) –1

29. Если (x₀, y₀) – решение системы линейных уравнений



тогда y₀ + x₀ равно

1) 3

+2) –3

3) –1

4) 1

30. Пусть задан вектор . Тогда длина вектора равна:

1)

+2)

3)

4)

31. Пусть задан вектор . Тогда длина вектора равна:

1)

2)

+3)

4)

32. Пусть задан вектор . Тогда длина вектора равна:

1)

+2)

3)

4)

33. Пусть задан вектор . Тогда длина равна:

+1)

2)

3)

4)

34. Пусть задан вектор . Тогда длина равна:

1)

2)

3)

+4)

35. Расстояние между точками A(1, 2) и B(–2, –2) равно…

1) 1

2) 10

3) 6

+4) 5

36. Расстояние между точками A(2, 7) и B(8, –1) равно…

1) 17

+2) 10

3) 6

4) 1

37. Расстояние между точками A(3, 2) и B(7, –1) равно…

1) 1

2) –7

+3) 5

4) 6

38. Расстояние между точками A(1, 2) и B(9, –4) равно…

1) 4

2) 1

3) 6

+4) 10

39. Расстояние между точками A(–1, 2) и B(–4, 6) равно…

1) 6

2) 10

+3) 5

4) 1

40. Векторы и перпендикулярны, если k равно…

1) –3

2) 2

+3) 3

4) –2

41. Векторы и перпендикулярны, если k равно…

1) –4

2) 4

3) –5

+4) 5

42. Векторы и перпендикулярны, если k равно…

1) 3

2) –6

+3) 6

4) –3

43. Векторы и перпендикулярны, если k равно…

1) 8

2) –8

3) –16

+4) 16

44. Векторы и перпендикулярны, если k равно…

+1) 12

2) 6

3) –12

4) –6

45. Векторы и коллинеарны, если k равно…

+1) –2

2) 1

3) 2

4) –1

46. Векторы и коллинеарны, если k равно…

1) –10

2) 10

3) 5

+4) –5

47. Векторы и коллинеарны, если k равно…

+1) 9

2) 6

3) –9

4) –6

48. Векторы и коллинеарны, если k равно…

1) 2

+2) –4

3) 4

4) -2

49. Векторы и коллинеарны, если k равно…

+1) 4

2) 2

3) –4

4) –2

50. Найдите скалярное произведение векторов и

+1) 17

2) 16

3) –13

4) 19

51. Найдите скалярное произведение векторов и

1) 17

2) 16

3) –9

+4) 21

52. Найдите скалярное произведение векторов и

1) 7

+2) 6

3) –9

4) –2

53. Найдите скалярное произведение векторов и

1) 7

2) 6

3) –9

+4) –11

54. Найдите скалярное произведение векторов и

1) 3

+2) 1

3) 9

4) –2

55. Найдите скалярное произведение векторов и

1) –9

+2) –6

3) 9

4) 3

56. Найдите скалярное произведение векторов и

1) –6

2) 1

3) 6

+4) –3

57. Даны векторы и . При каком значении числа m

+1) –1

2) 3

3) 2

4) –2

58. Даны векторы и . При каком значении числа m

1) 3

+2) –3

3) 2

4) –2

59. Даны векторы и . При каком значении числа m

1) 3

2) 2

+3) –3

4) –2

60. Даны векторы и . При каком значении числа m

1) 4

2) –3

+3) 2

4) –2

61. Даны векторы и . При каком значении числа m

1) 3

2) –1

3) 2

+4) –2

62. Даны векторы и . При каком значении числа m

1) 3

+2) –2

3) 2

4) –3

63. Даны векторы и . При каком значении числа m

1) 6

+2) –6

3) 2

4) –2

64. Даны векторы и . При каком значении числа m

+1) 6

2) –6

3) 2

4) –2

65. Даны векторы и . При каком значении числа m

1) 6

2) –6

+3) 4

4) –4

66. Прямая проходит через точки О(0;0) и В(–8;–2). Тогда ее угловой коэффициент равен:

+1)

2) 4

3)

4) –4

67. Прямая проходит через точки О(0;0) и В(–3;9). Тогда ее угловой коэффициент равен:

+1) –3

2) 9

3) 3

4) –9

68. Прямая проходит через точки О(0;0) и В(–14;2). Тогда ее угловой коэффициент равен:

+1)

2) 7

3)

4) –7

69. Прямая проходит через точки О(0;0) и В(25;15). Тогда ее угловой коэффициент равен:

1)

+2)

3)

4)

70. Координата точки , принадлежащей плоскости , равна

1) 7

2) 5

3) 3

+4) 1

71. Координата точки , принадлежащей плоскости , равна

1) 5

2) 3

3) 6

+4) 2

72. Координата точки , принадлежащей плоскости , равна

+1) 2

2) 3

3) 4

4) 1

73. Координата точки , принадлежащей плоскости , равна

1) 4

2) 1

3) 2

+4) 3
74. Тригонометрическая форма комплексного числа :

1)

2)
+3)
4) .
75. Тригонометрическая форма комплексного числа :

1)

+2)

3)

4) .

76. Тригонометрическая форма комплексного числа :

1)

2)

3)

4)

77. Тригонометрическая форма комплексного числа :

1)

2)

3)

4)
78. Тригонометрическая форма комплексного числа :

1)

2)

3)

4)

79. Тригонометрическая форма комплексного числа :

1)

2)

3)

4)

80. Тригонометрическая форма комплексного числа :

1)

2)

3)

4)
81. Найти , если

+1) ;

2) ;

3) ;

4) .
82. Найти , если

1)

2)

3)

4)

83. Найти , если

1)

2)

3)

4)

84. Найти , если

1)

2)

3)

4)

85. Найти , если

1)

2)

3)

4)

86. Найти , если

1)

2)

3)

4)

87. Найти , если

1)

2)

3)

4)

88. Найти , если

1)

2)

3)

4)

89. Найти , если

1)

2)

3)

4)

90. Найти , если

1)

2)

3)

4)
91. Определитель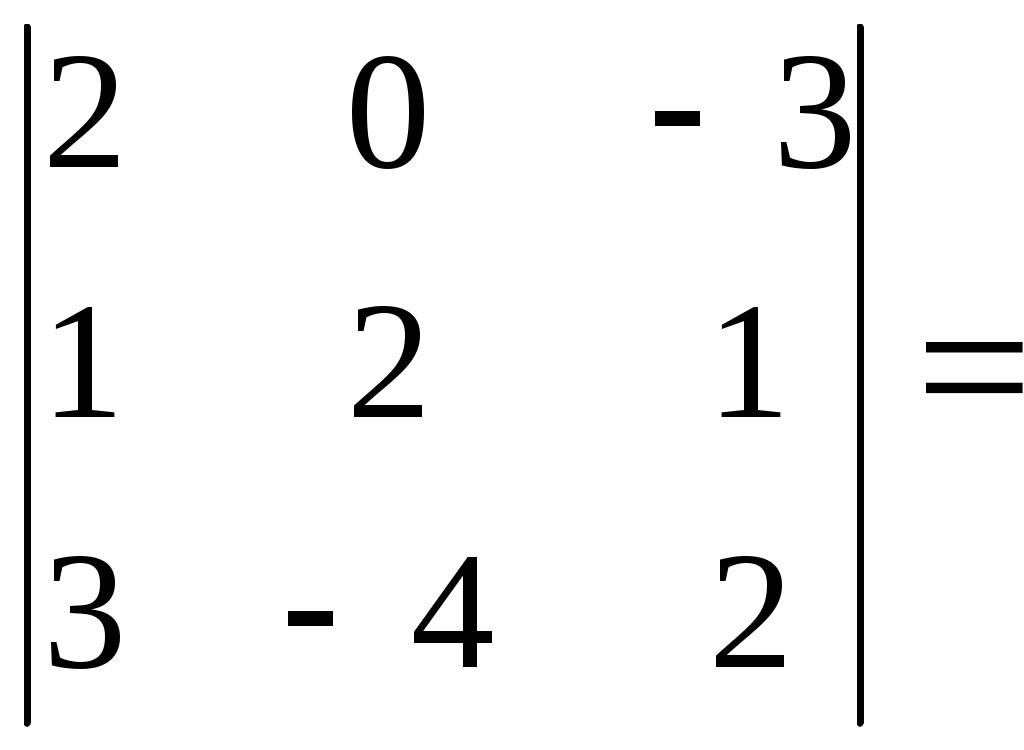

1)

2)

3)

4)

92. Определитель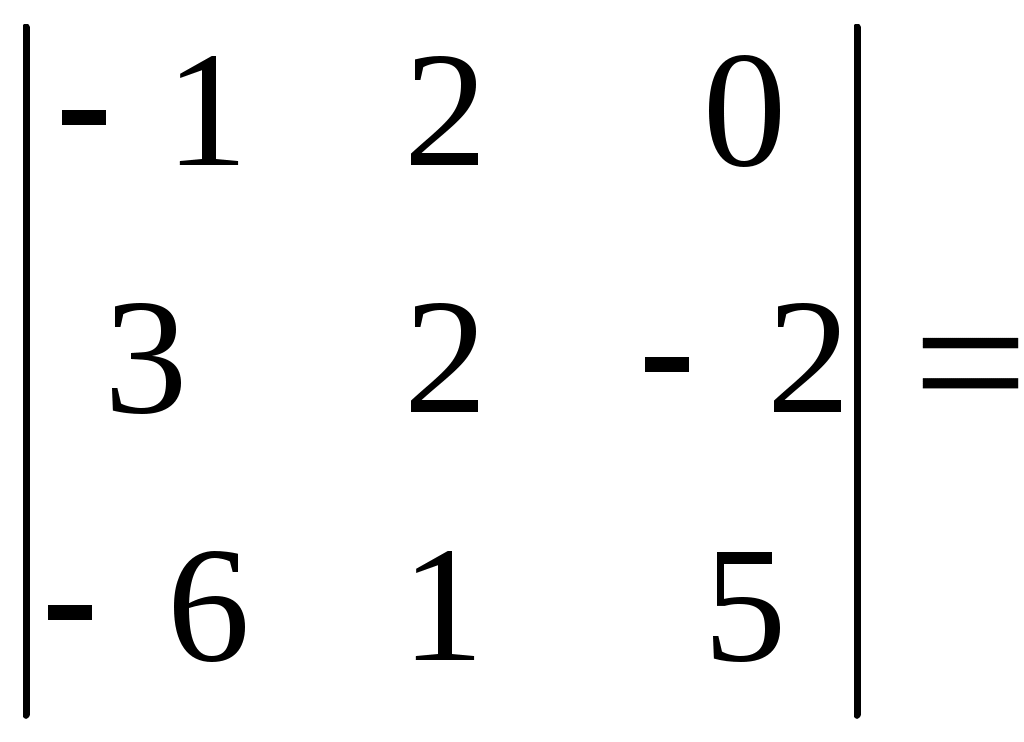

1)

2)

3)

4)
93. Определитель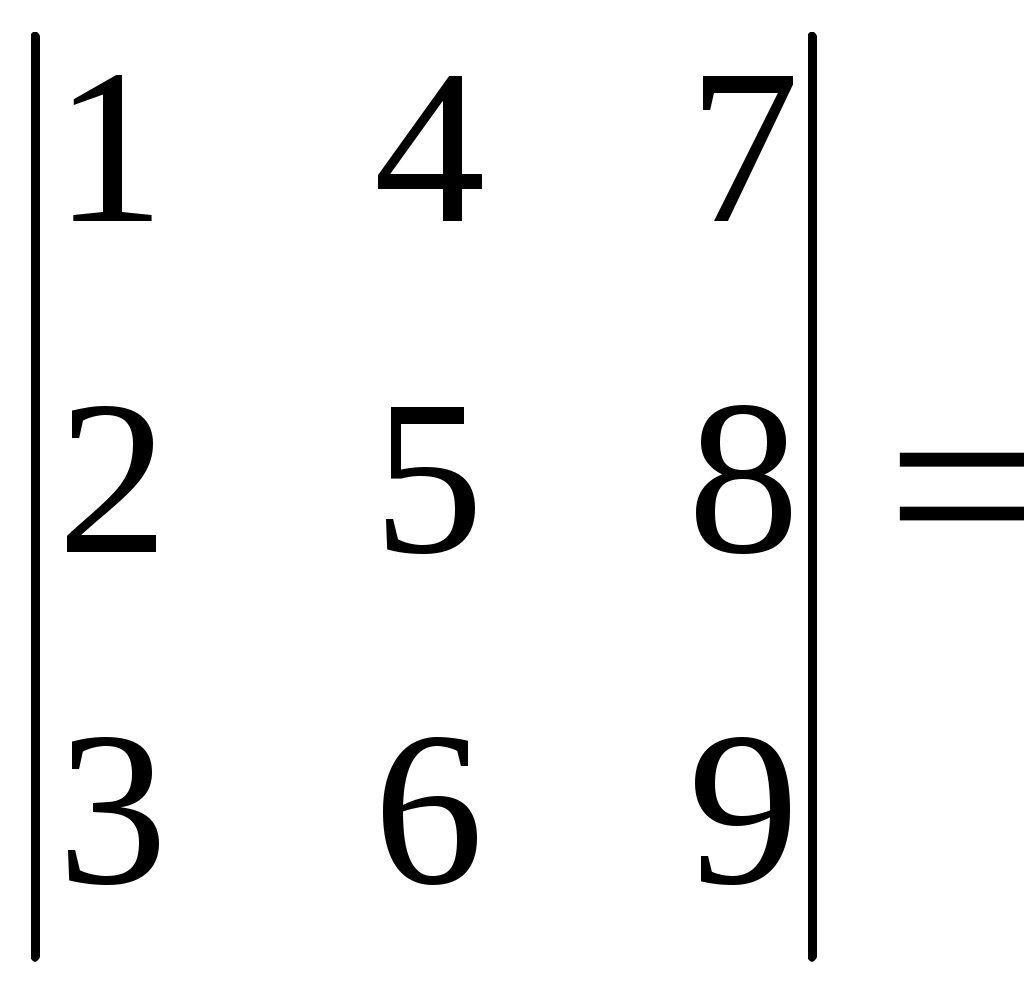

1)

2)

3)

4)
94. Определитель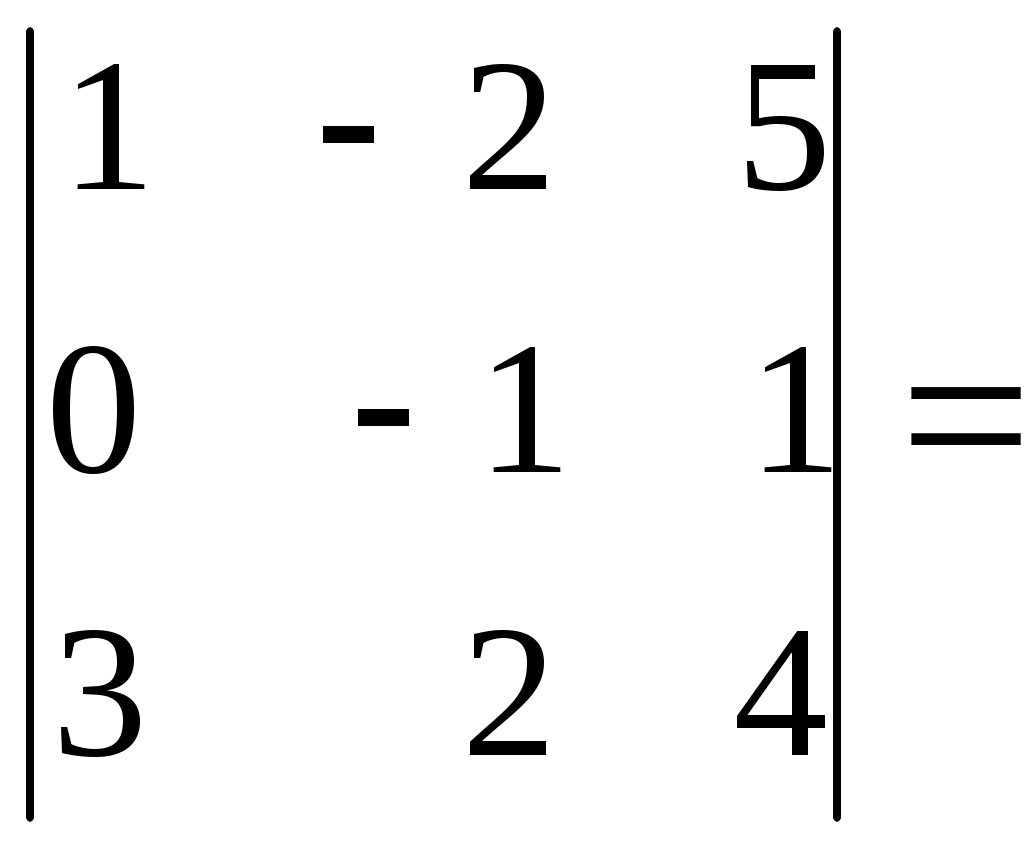

1)

2)

3)

4)
95. Определитель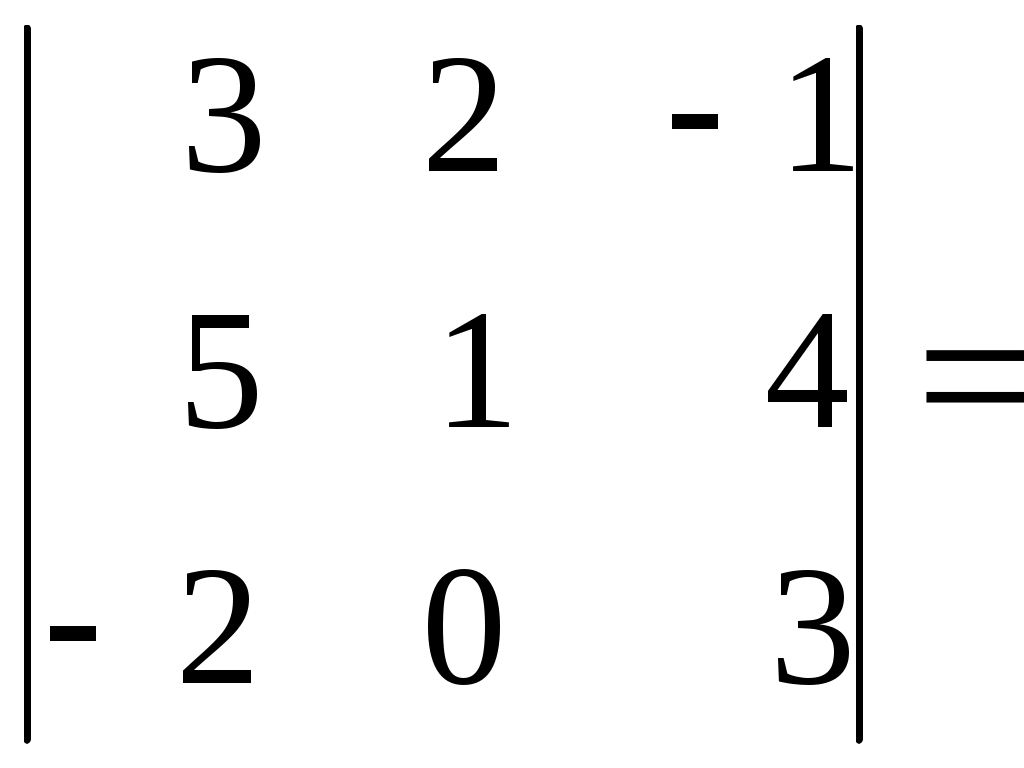

1)

2)

3)

4)
96. Определитель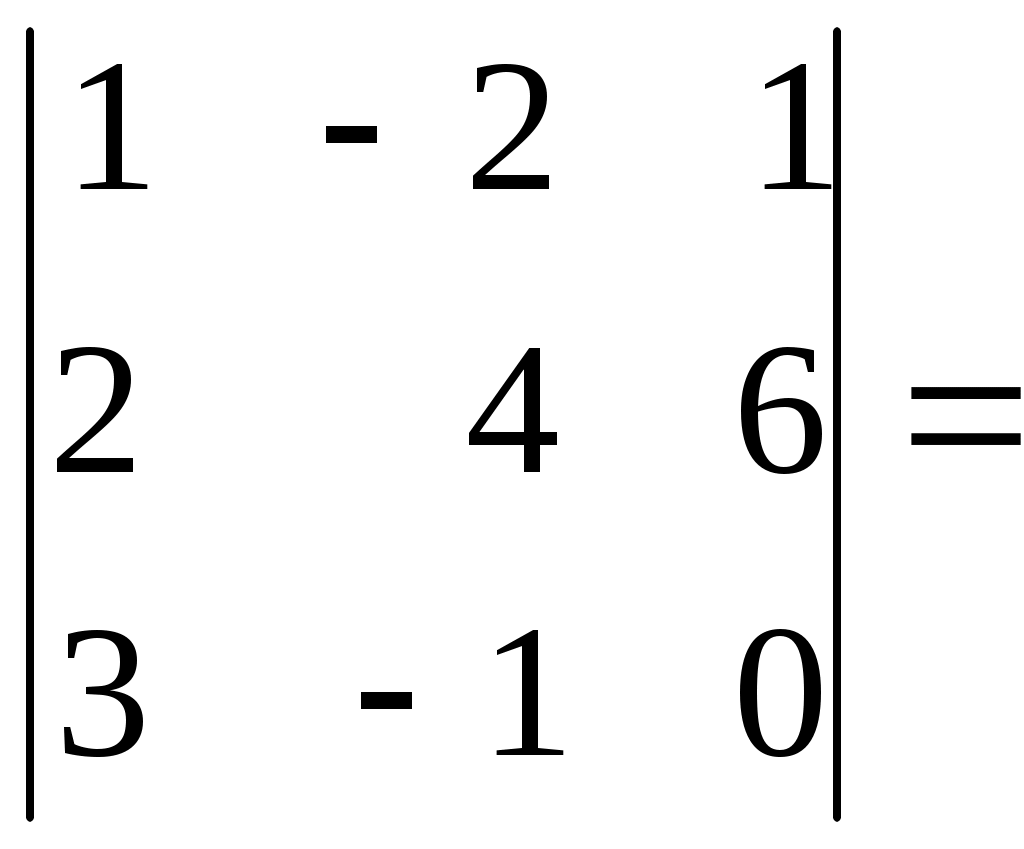

1)

2)

3)

4)
97. Определитель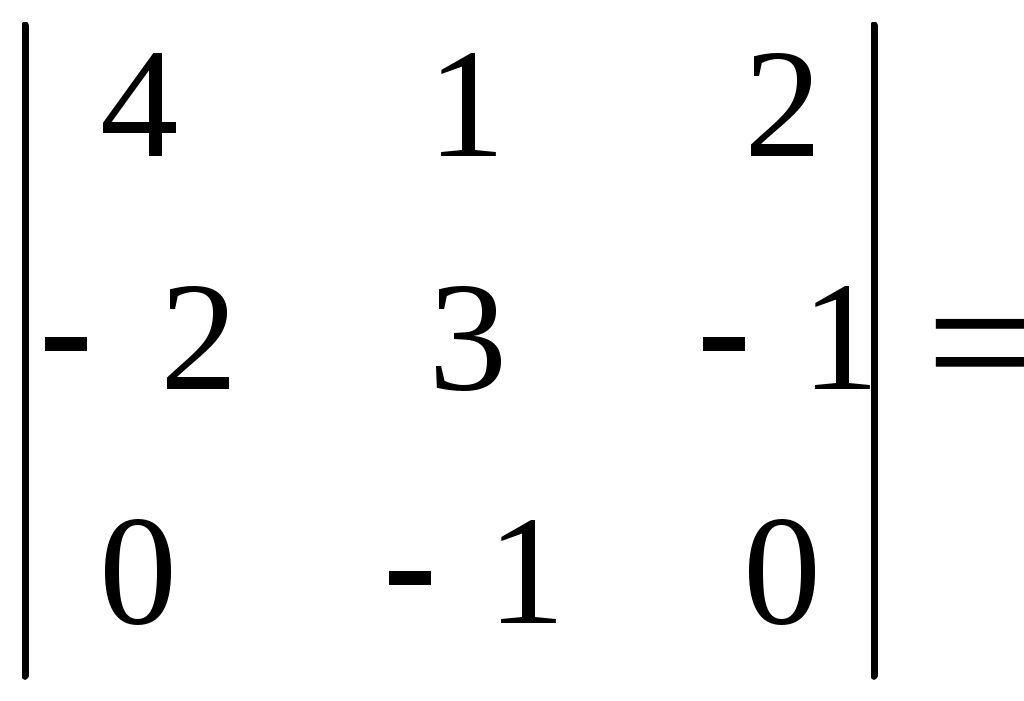

1)

2)

3)

4)

97. Определитель 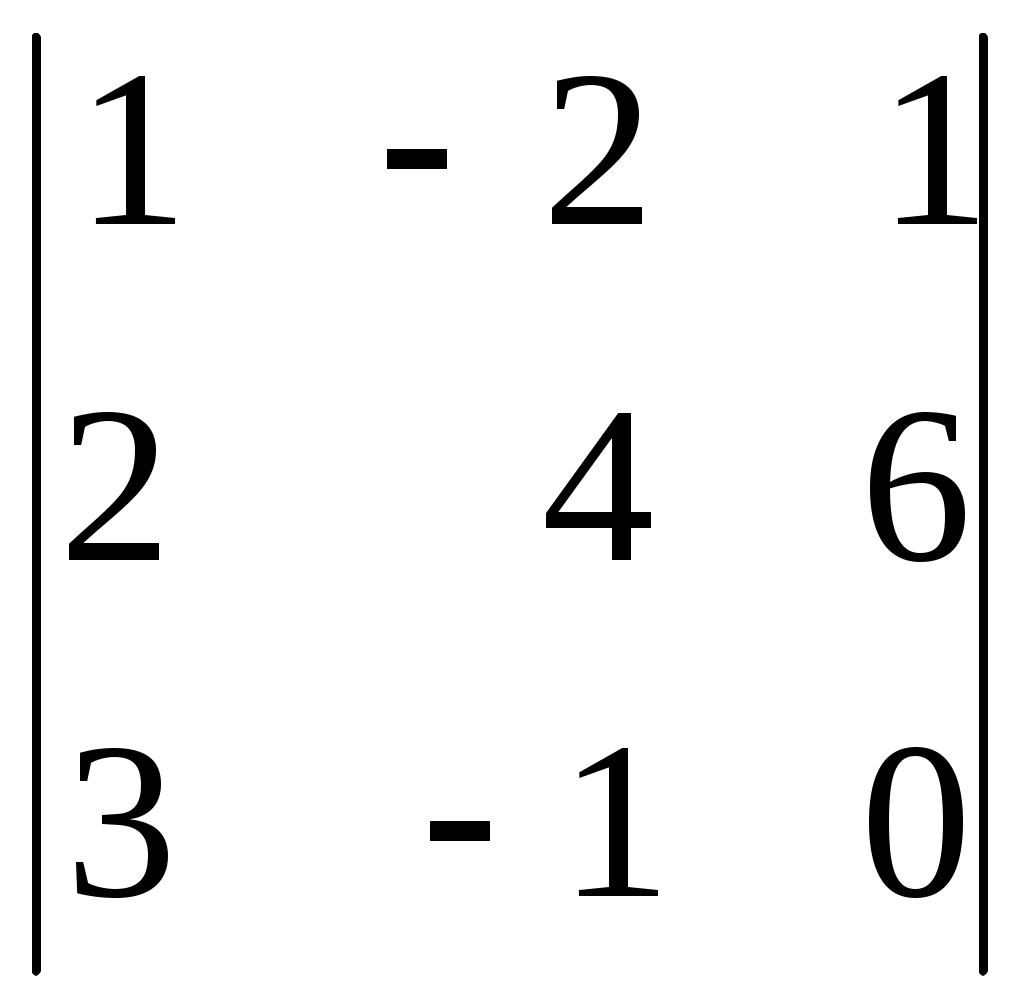. Алгебраическое дополнение

1)

2)

3)

4)

98. Определитель 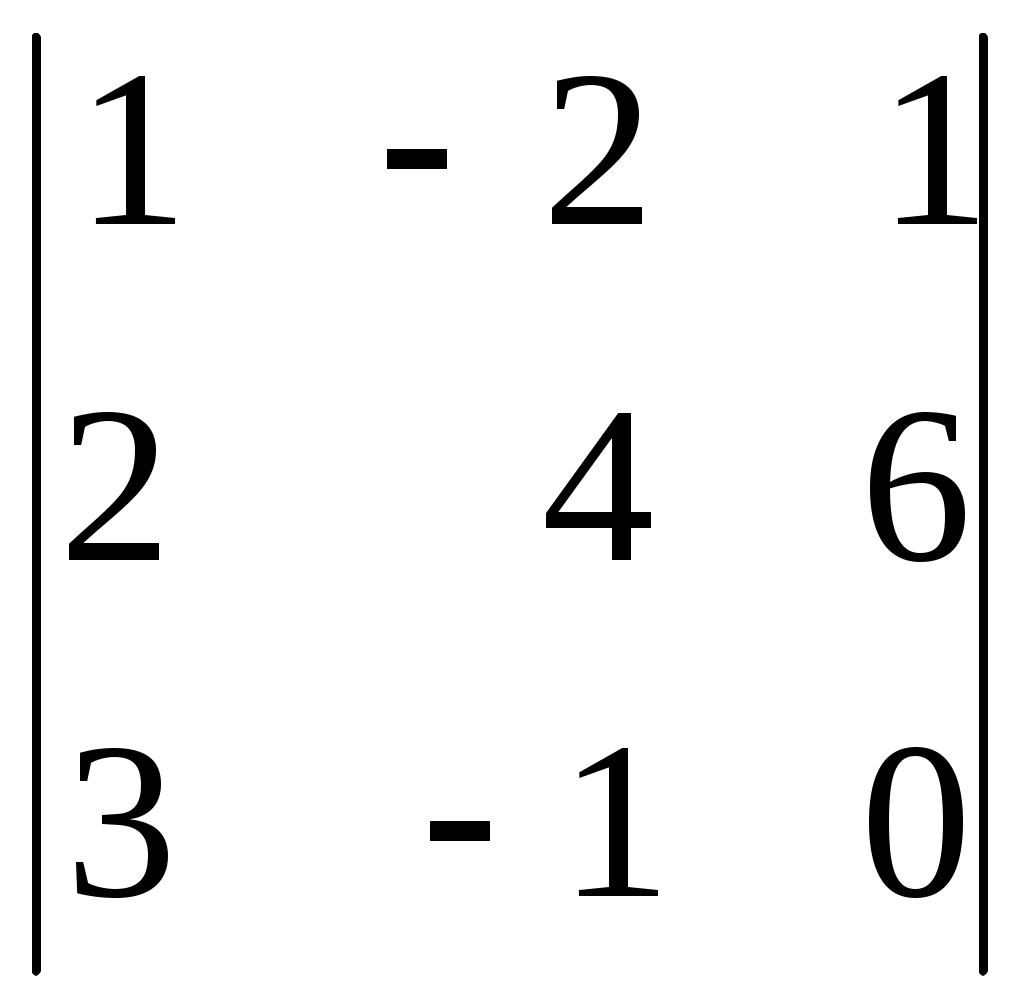. Алгебраическое дополнение

1)

2)

3)

4)
99. Определитель 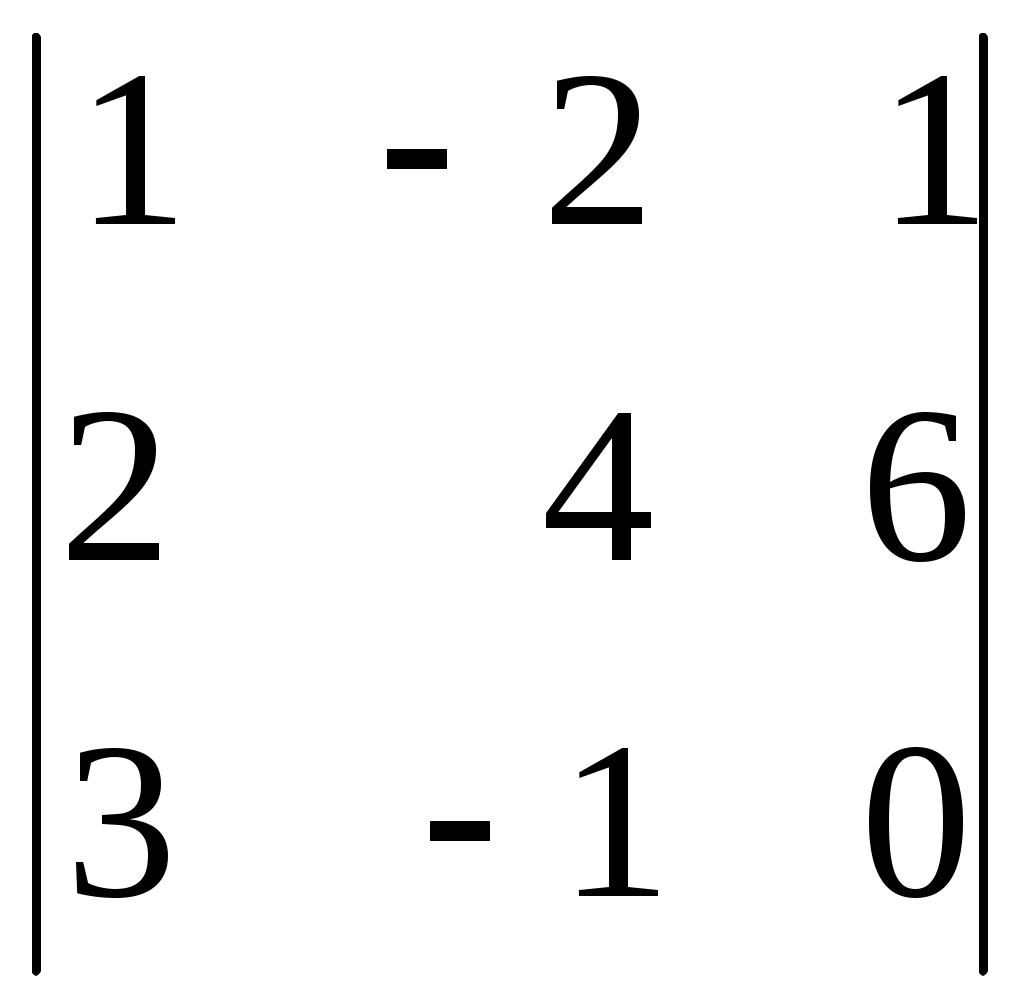. Алгебраическое дополнение

1)

2)

3)

4)
100. Определитель 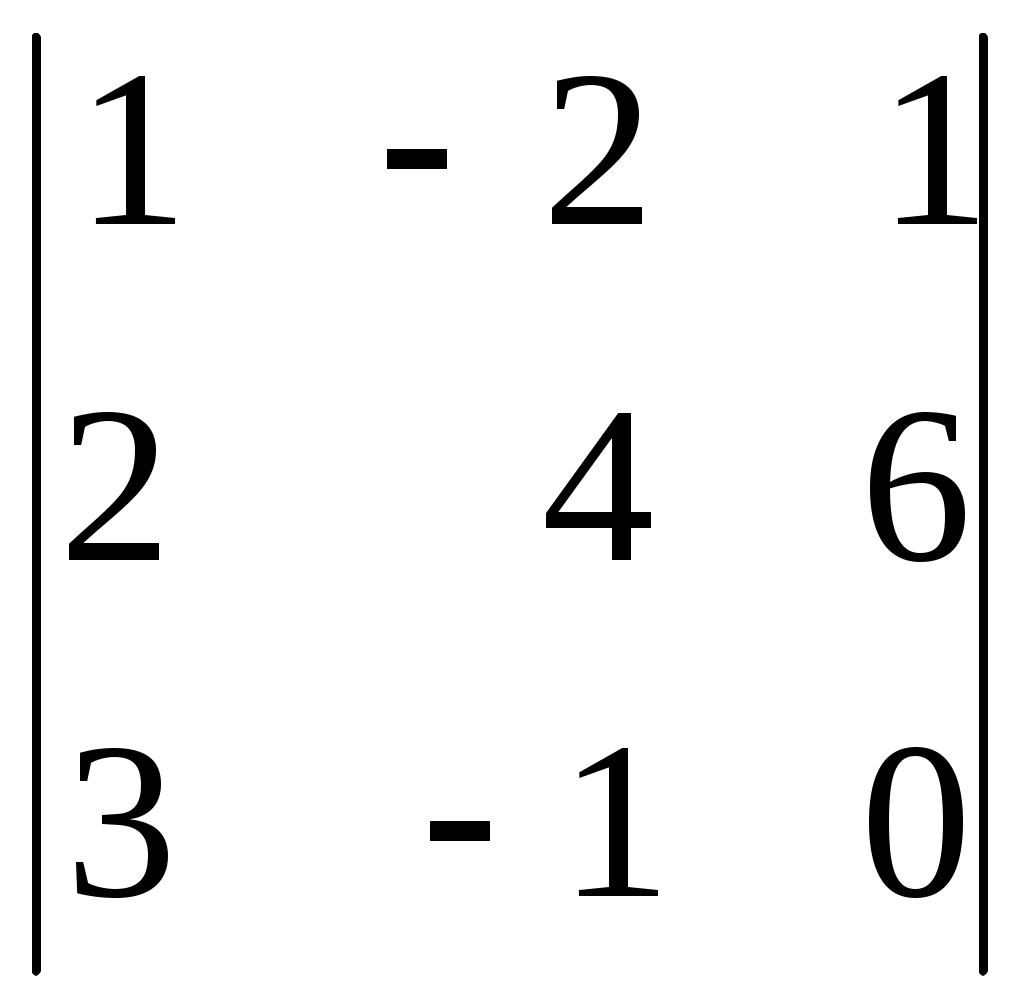. Алгебраическое дополнение

1)

2)

3)

4)