Теоретическая часть Две матрицыАиВ называются равными, если

• Название: Теоретическая часть Две матрицыАиВ называются равными, если
• Дата: 12.01.2022
• Размер: 0.82 Mb.
• Имя файла: Matem_1kurs_1_sem_Gazizov_E_R (2).doc
• Тип: Документы; #329096
• страница: 1 из 2

Теоретическая часть

1. Две матрицы А и В называются равными, если

1) они имеют одинаковые число строк и число столбов;

+2) они имеют одинаковые число строк и число столбов, и их соответствующие элементы равны;

3) они имеют одинаковые число строк и число столбов, и у них равны определители.

2. Матрицей называется

1) число, вычисляемое по определенным правилам;

2) система линейных уравнений с переменными;
+3) прямоугольная таблица чисел, содержащая строк одинаковой длины.

3. Матрица называется единичной, если

1) она имеет вид ;

+2) она имеет вид ;

3) она имеет вид .

4. Матрица называется нулевой, если

1) ее определитель равно нулю ;

2) суммы элементов каждой строки равны нулю;

+3) она имеет вид .

5. Матрица называется транспонированной к исходной матрице, если

1) равны их определители;

2) их произведение равно единичной матрице;

+3) ее столбцами являются строки исходной матрицы.

6. При транспонировании матрицы несправедливым является свойство

1) ;

2) ;

+3) ;

4) .

7. Матрица называется квадратной, если

1) все элементы строк (столбцов) не равны нулю;

2) число строк не равно числу столбцов;

+3) число строк равно числу столбцов;

4) все элементы строк (столбцов) равны единице.

8. При умножении двух матриц должно соблюдаться условие

1) число столбцов первой матрицы равно числу столбцов второй матрицы;

2) число строк первой матрицы равно числу столбцов второй матрицы;

+3) число столбцов первой матрицы равно числу строк второй матрицы.

4) число строк первой матрицы не равно числу столбцов второй матрицы.

9. Две матрицы называются эквивалентными, если

1) их произведение равно единичной матрице;

+2) одна из них получается из другой с помощью элементарных преобразований;

3) они имеют одинаковые число строк и число столбов,
и у них равны определители.

10. Определитель вычисляется по формуле:

1) ;

2) ;

3) ;

+4) .

11. Если элементы двух столбцов (строк) определителя пропорциональны, то определитель равен:

1) удвоенному значению определителя, получаемому при вычеркивании соответствующих столбцов (строк);

+2) нулю;

3) сумме произведений элементов этих столбцов (строк) на их алгебраические дополнения;

4) единице.

12. Если элементы двух столбцов (строк) определителя поменять местами, то определитель

1) будет равен удвоенному значению определителя, получаемому при вычеркивании соответствующих столбцов (строк);

2) будет равен нулю;

+3) поменяет знак на противоположный;

4) будет равен единице.

13. Матрица А^-1 называется обратной по отношению к квадратной матрице А, если она удовлетворяет условию

1) ;

2) ;

+3) , где Е – единичная матрица;

4) .

14. Любая невырожденная матрица имеет обратную следующего вида:

+1)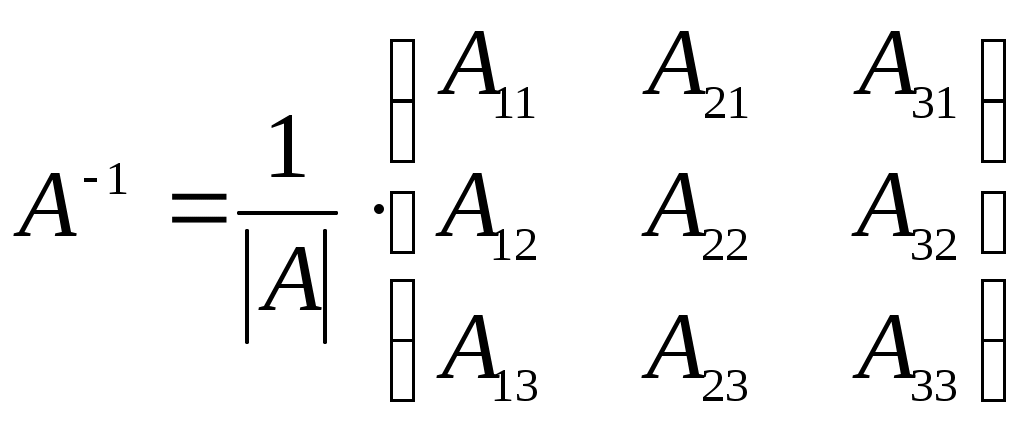

2)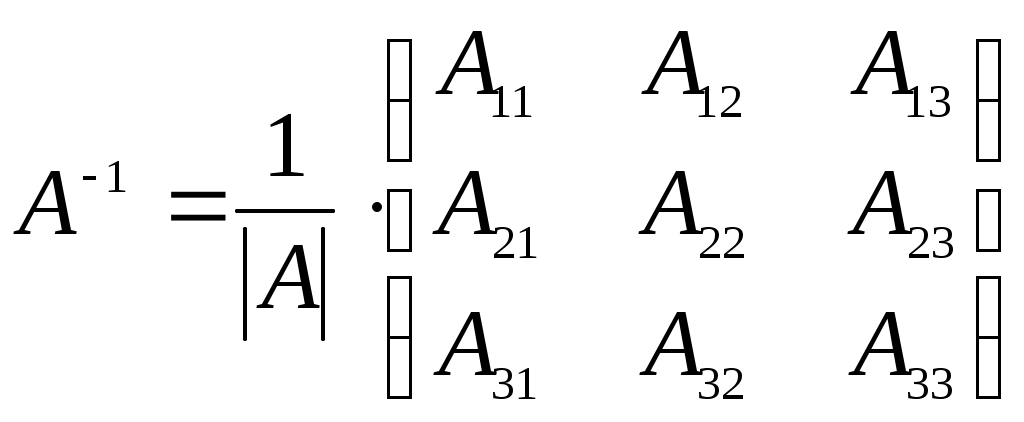

3)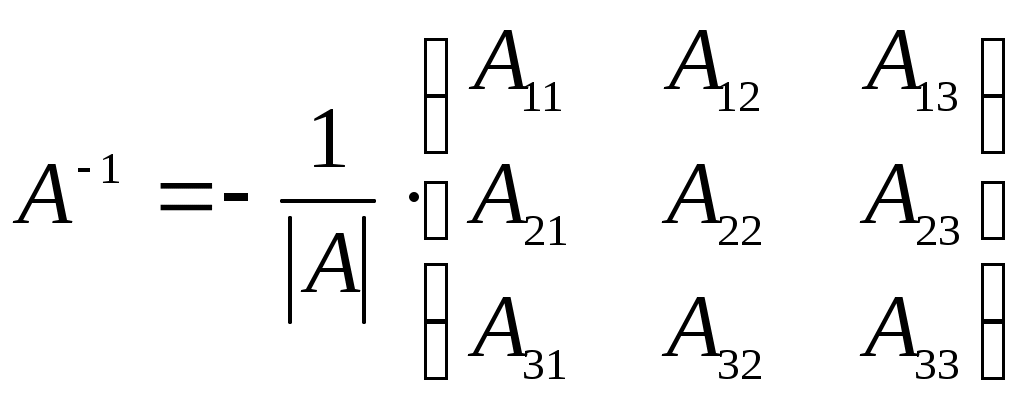

15. Решение матричного уравнения А∙Х = В имеет вид

+1) Х = А^-1∙В;

2) Х = В∙А^-1;

3) Х = А^-1∙В^-1;

4) Х = Е∙А^-1.

16. Система линейных алгебраических уравнений называется совместной, если

1) она не имеет ни одного решения;

+2) она имеет хотя бы одно решение;

3) если свободные члены этой системы равны нулю;

4) если ранг матрицы этой системы равен 1.

17. Система линейных алгебраических уравнений называется несовместной, если

+1) она не имеет ни одного решения;

2) она имеет хотя бы одно решение;

3) если свободные члены этой системы равны нулю;

4) если ранг матрицы этой системы равен 1.

18. Система линейных алгебраических уравнений называется определенной,

если

1) ранг этой системы равен 1;

+2) если она имеет единственное решение;

3) если она имеет более одного решения;

4) если она не имеет решений.

19. Система линейных алгебраических уравнений называется неопределенной, если

1) ранг этой системы равен 1;

2) если она имеет единственное решение;

+3) если она имеет более одного решения;

4) если она не имеет решений.

20. Три вектора в пространстве называются компланарными, если они

1) имеют одинаковую длину;

2) два из них перпендикулярны третьему;

+3) принадлежат одной или параллельным плоскостям;

4) лежат в разных плоскостях.

21. Два вектора и называются коллинеарными, если они…

1) лежат в одной плоскости или на параллельных плоскостях;

+2) лежат на одной прямой или на параллельных прямых;

3) имеют одинаковую длину;

4) имеют разные длины.

22. Два вектора и называются равными, если они…

+1) коллинеарные, имеют одинаковую длину и направление;

2) имеют одинаковую длину;

3) имеют одинаковую длину и коллинеарные;

4) имеют одинаковую длину и лежат в одной плоскости.

23. Скалярное произведение двух векторов и вычисляется по формуле:

+1) ;

2) ;

3) ;

4) .

24. Косинус угла между векторами и вычисляется по формуле:

1) ;

+2) ;

3) ;

4) .

25. Условием перпендикулярности двух векторов является

+1) ;

2) ;

3) ;

4) .

26. Условием коллинеарности двух векторов является

1) ;

2) ;

+3) .

27. Векторным произведением двух векторов и называется:

+1) третий вектор , длина которого численно равна площади параллелограмма, построенного на векторах и как на сторонах, направленный перпендикулярно плоскости, образованной векторами и и причем, так, что если смотреть из конца вектора , то поворот вектора к вектору будет происходить против часовой стрелки и кратчайшим путем.

2) третий вектор , и равный площади треугольника, построенного на векторах и .

3) третий вектор , длина которого равна объему пирамиды, построенной на векторах , и ;

4) третий вектор , длина которого равна объему параллелепипеда, построенного на векторах , и ;

28. Формула вычисления векторного произведения вектора н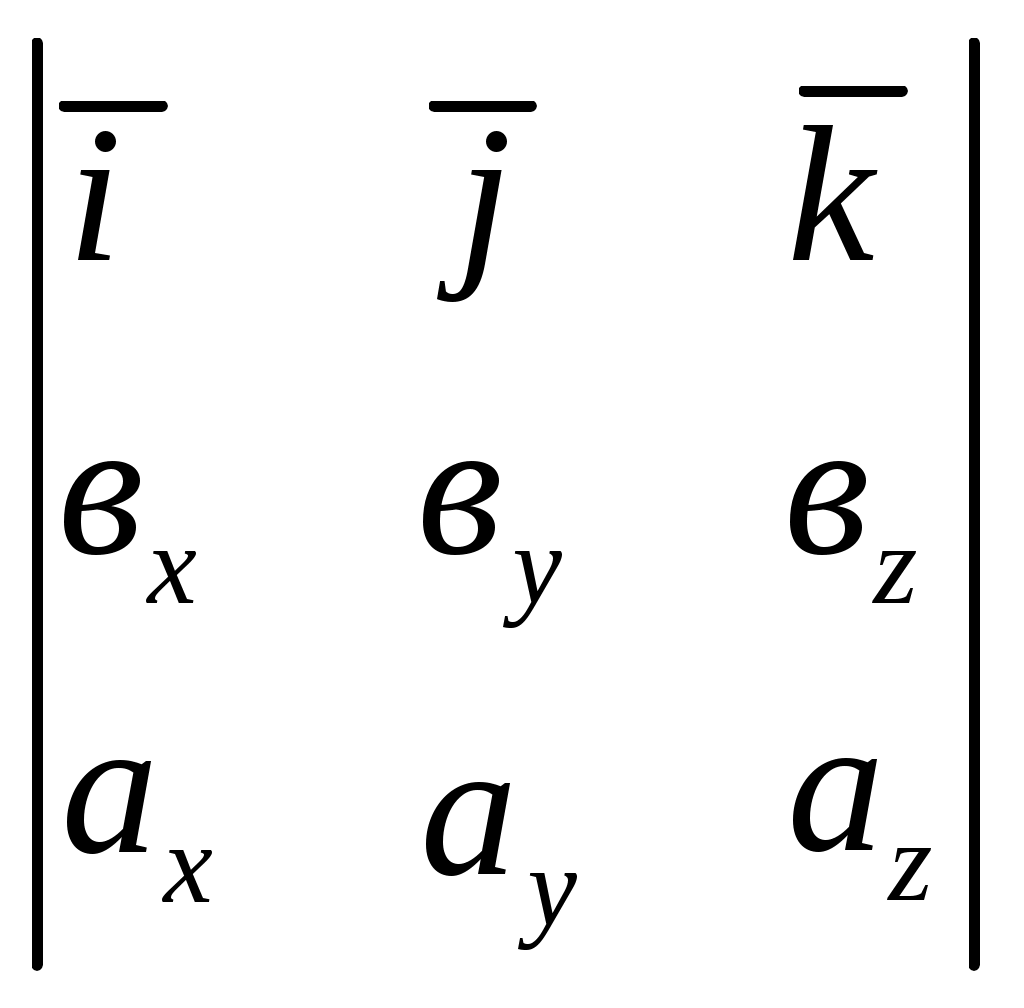а вектор имеет вид:

1) ;

+2) ;

3) ;

4) .

29. Смешанным произведением трех векторов , и называется:

1) скалярное произведение суммы векторов и на вектор ;

2) векторное произведение вектора на сумму векторов и ;

3) скалярное произведение вектора на сумму векторов и ;

+4) скалярное произведение векторного произведения векторов и на вектор .

30. Смешанное произведение трех векторов , и вычисляется по формуле:

+1)

2)

3) ;

4)

31. Геометрический смысл смешанного произведения трех векторов заключается в том, что оно равно:

1) длине диагонали параллелепипеда, построенного на этих векторах;

+2) объему параллелепипеда, построенного на этих векторах;

3) длине вектора, равного сумме этих трех векторов;

4) площади параллелограмма, построенного на двух векторах перпендикулярно третьему вектору.

32. Формула вычисления объема треугольной пирамиды имеет вид:

1) ;

2) ;

+3) ;

4) .

33. Если прямые и перпендикулярны, то выполняется следующее равенство:

1) ;

+2) ;

3) .

34. Если прямые и параллельны, то выполняется следующее равенство:

1) ;

2) ;

+3) .

35. Расстояние от точки до прямой вычисляется по формуле:

1) ;

2) ;

+3) .

36. Уравнение прямой, проходящей через данную точку в данном направлении имеет вид:

1) ;

2) ;

3) ;

+4) ;

37. Уравнение прямой с нормальным вектором имеет вид:

1) ;

+2) ;

3) ;

4) ;

38. Уравнение прямой, проходящей через две точки находится по формуле:

1) ;

2) ;

+3) ;

4) ;

39. Угол между прямыми, заданными в виде и , находится по формуле:
+1) ;

2) ;

3) .

40. Проверить параллельность прямых, заданных в виде и , можно, используя формулу:

1) ;

2) ;

+3) .
41. Если прямые и перпендикулярны, то выполняется следующее равенство:

1) ;

+2) ;

3) .

42. Если прямые и параллельны, то выполняется следующее равенство:

1) ;

2) ;

+3) .
43. Выберите верное утверждение:

+1) Если уравнение плоскости имеет вид то она параллельна оси ;

2) Если уравнение плоскости имеет вид то она проходит ось ;

3) Если уравнение плоскости имеет вид то она параллельна плоскости .

44. Выберите верное утверждение:

1) Если уравнение плоскости имеет вид то она проходит ось ;

2) Если уравнение плоскости имеет вид то она параллельна плоскости .

+3) Если уравнение плоскости имеет вид то она параллельна оси ;

45. Выберите верное утверждение:

1) Если уравнение плоскости имеет вид то она проходит ось ;

2) Если уравнение плоскости имеет вид то она параллельна плоскости .

+3) Если уравнение плоскости имеет вид то она параллельна оси ;

46. Эксцентриситет эллипса удовлетворяет неравенству:

+1)

2)

3)

47. Эксцентриситет гиперболы удовлетворяет неравенству:

1)

+2)

3)

48. Уравнения асимптот гиперболы имеют вид:

+1)

2)

3)

49. Умножение комплексных чисел и вычисляется по формуле

+1)

2)

3)

50. Деление комплексных чисел и вычисляется по формуле

1)

+2)
3)

51. Корень n – ой степени из комплексного числа вычисляется по формуле:

1)

2)

3)

+4)

52. Формула Муавра имеет вид:

+1)

2)

3)

4)