ТЕОРЕТИЧЕСКИЕ АСПЕКТЫ ОБУЧЕНИЯ МАТЕМАТИКЕ В ПЕРВОМ КЛАССЕ. Статья Шевченко О.Г.. Теоретические аспекты обучения математике в первом классе
 Скачать 293.36 Kb. Скачать 293.36 Kb.
|
|
ТЕОРЕТИЧЕСКИЕ АСПЕКТЫ ОБУЧЕНИЯ МАТЕМАТИКЕ В ПЕРВОМ КЛАССЕ Подготовила Шевченко Оксана Геннадьевна, учитель начальных классов Муниципального образовательного учреждения СОШ №8 (МОУ СОШ №8) г. Люберцы Московского муниципального округа Содержание Введение Глава 1. Теоретические аспекты обучения математике в первом классе Основы изучение математики в первом классе Понятие предметных моделей Глава 2. Разработка конспектов фрагментов уроков математики в 1-м классе с применением предметных моделей Заключение Библиографический список. Введение Основой всего школьного обучение является обучение в начальной школу, и особенно в первом классе. Именно при поступлении ребенка в школу начинается закладка образовательного фундамента. Дети начинают учиться, начинаю осознавать значимость учения, значимость серьезного и последовательного подходу к обучению. Сточки зрения государственных стандартов, начальное образование формирует ключевые составляющие учебной деятельности ребенка. Формируется комплекс мотивов учебного и познавательного характера, способность принятия, сохранения и реализации учебных целей. Первоклассники учатся составлять план своих учебных действий, контролировать их и давать свою собственную оценку. Для реализации всего выше перечисленного в начальной школе существует много учебных предметов. Одним из них является математика, которая учит первоклассников математическому языку, формирует у них способность описывать все, что их окружает именно этим языком. На уроках математики дети учатся решать задачи, сопоставляя их с реальной жизнью. Освоение математики развивает в учащихся основы логического подхода к окружающим вещам, формирует способность применять на практике умение измерять и вычислять. Таким образом создается база для успешной организации процесса обучения учащихся в начальной школе. Стоит отметить, что предмет математики является одним из сложных в начальном обучении. Не все дети справляются с освоением математических приёмов вычисления и измерения. Поэтому в задачи учителя входит создание наиболее благоприятных условий, чтобы каждый ученик на уроке, в соответствии со своими индивидуальными способностями. Наряду с условиями необходимы продуктивные методы, формы, приемы, позволяющие наиболее эффективно объяснить тот или иной материал на уроке математики. В первом классе одним из таких приемов является использование предметных моделей. Такой прием может сделать урок не только продуктивнее, но и интереснее, эмоционально насыщеннее. Эмоционально яркий урок надолго сохраняется в памяти ребенка, что способствует развитию интереса к урокам математики. К тому же, учитывая, что у младших школьников большинство понятий формируется на основе наглядно-образного мышления, предметные модели как нельзя лучше, могут помочь наглядно объяснить новый материал, продемонстрировать связь математических действия с действиями в реальной жизни. Однако, не все учителя начальных классов используют предметные модели на уроках математики в первом классе в связи с тем, что проведение такого урока требует тщательной и объемной подготовки. Поэтому актуальным становится осознание педагогами необходимости такой работы в целях не только развития интереса первоклассников к уроку математики, нов целях усвоения ими основных математических действий, в целях формирования метапредметных компетенций, основы всего последующего обучения. Объект данного курсового исследования – процесс обучения математике в 1-м классе. Предмет исследования – организация обучения математике в 1-м классе с использованием предметных моделей Цель исследования – разработать комплект конспектов фрагментов уроков математики для 1-го класса с применением предметных моделей. Для достижения поставленной цели необходимо решить следующие задачи: Изучить специфику обучения математике в 1-м классе Рассмотреть сущность предметных моделей Разработать конспекты фрагментов уроков математики в 1-м классе с применением предметных моделей Методы исследования: теоретический (анализ педагогической литературы по теме исследования), научный (анализ, синтез, обобщение полученной информации), практический (разработка конспектов). Практическая значимость курсового исследования заключается в том, что результаты могут быть использованы педагогами начальных классов, студентами педагогических институтов при подготовке к урокам математики в 1-м классе. Глава 1. Теоретические аспекты обучения математике в первом классе 1.1 Основы изучение математики в первом классе Начальное образование имеет в своем содержание большое число составляющих, одним из которых является обучение математике. Велика роль данного учебного предмета в формировании первоклассников умения учиться. Если говорит о целевом направлении обучения математики, то этот предмет направлен на: Формирование у первоклассников основы начальных математических знаний, которые выстраиваются в логичную систему. Математическое развитие младших школьников. Развитие устойчивого интереса к урокам математики, что будет способствовать развитию умственной деятельности в целом. Раскроем, что же входит в понятие умственной деятельности, с каких основ начинается ее развитие. Уроки математик в первом классе учат детей анализировать и сравнивать, распределять предметы п группам и классам, находить связи между предметами и явлениями, рассуждать логически. Иными словами, на уроках математики в первом классе происходит усвоение знаний и способов действий обобщенного характера. Говоря языком ФГОС НОО, у первоклассников формируются универсальные учебные действия, УУД. Сформированные УУД позволяют в дальнейшем усваивать предметные знания, развивать интеллектуально, сопоставлять жизненные процессы и явления, самостоятельно искать информацию и усваивать ее, что и является умственной деятельностью. Иными словами, усвоенные знания на уроках математики в первом классе необходимы не только для того, чтобы успешно усваивать математический материал в последующих классах, но и для решения многих других задач, которые ставит перед нами жизнь. Согласно ФГОС НОО, обучение математике в первом классе призвано решить следующий комплекс задач: через усвоение несложных математических способов познания окружающей действительности формирование у младших школьников умения самостоятельно интеллектуально мыслить: устанавливать, описывать, моделировать и объяснять количественные и пространственные отношения; развитие мыслительных умений логического, знаково-символического и алгоритмического характера; развитие пространственного воображения; развитие способности объяснять процессы и явления математическим языком; формирование системы начальных математических знаний и умений их применять для решения учебно-познавательных и практических задач; формирование умения находить необходимую информацию в различных источниках и работать с ней; развитие познавательных способностей; воспитание стремления не только усвоению математических знаний, но и к их накоплению и расширению; формирование критичности мышления; развитие умений высказывать свое суждение, находить аргументы в его пользу, отставать свое мнение, давать ему оценку, так же как и мнениям других детей. Перечисленные задачи при их реешении будут способствоать развитию у первоклассников умения пощнавать мир универсально, усвоению начальных математических знаний, умения связывать математические знания с окружающей действительностью, находить взаимосвязь математических понятий и понятий, усвоенных на других учебных предметах. Кроме этого, первоклассники станут расширять свои математические знания, применяя усвоенные на уроках математики знания в своей жизни. Начальный математический курс можно назвать интегрированным, поэтму что в нем соединились и арифметика, и геометрия, и алгебра, верее их ключевые понятия. С предметами алгебра и геометрия учащиеся познакомятся гораздо позже в процессе обучения, но у же в первом классе они постигают основу математического обучения. Это позволит им лучше понять более сложный материал математических дисциплин, изучаемых в средней и старшей школе. Однако, данный факт не говорит о пропедевтическом характере начального курса математики. Начальный математический курс прежде всего развивает умение детей мыслить теоретически, планировать, анализировать, рефлексировать. В этом возрасте у детей происходит также становление потребности и мотивов к обучению. В связи с этим математическое образование в первом классе базируется на следующих методических принципах: принцип аналитического подхода при отборе материала с точки зрения его общеобразовательной ценности и необходимости изучения в первом классе; принцип связи с жизнью, то есть материал должен быть таким, чтобы его моно было применить на практике; принцип заинтересованности. Согласно Примерной основной образовательной программы начального образования в математическом курсе выделяется пять взаимосвязанных содержательных линий: элементы арифметики; величины и их измерение; логико-математические понятия; алгебраическая пропедевтика; элементы геометрии. Каждая линия содержит свои понятия. В целом понятийный аппарат состоит из четырех, которые вводятся без определений: число, отношение, величина, геометрическая фигура. Общее содержание обучения математике представлено в программе следующими разделами: «Число и счёт», «Арифметические действия и их свойства», «Величины», «Работа с текстовыми задачами», «Геометрические понятия», «Логико-математическая подготовка», «Работа с информацией». Опишем специфику содержания обучения математики в 1-м классе. Так, в первом классе формируются первоначальные представления о натуральном числе. Сначала учащиеся узнают. Как называются числа первого десятка, учатся назвать их в разном порядке. Затем первоклассников знакомят с пересчетом предметов на основе изученной последовательности натуральных чисел. Учащиеся учатся получать результат пересчитывания и записывать его цифрами. Одновременно с обучением пересчитыванию, первоклассники знакомятся с основами решения задач, оперируя различными предметами, выполняя различные с ними практические действия. Стоит отметить, что задача в данный период предстает перед детьми, как знакомая им жизненная ситуация, в которой надо посчитать предметы, как показано на рис.1.  Рис. 1 Задача из учебника М.И. Моро, С.И. Волковой «Математика. 1 класс» Подобные задания помогают накапливать учащимся практический опыт применения математических знаний, складывать и вычитать предметы, а впоследствии – умножать и делить. На втором этапе педагог направляет обучение на узнавание учащимися чисел, которые упоминаются в задаче. При выполнении решения ученики применяют фразы: «пять и три - это восемь», «пять без двух - это три», «три по два – это шесть», «восемь на два - это четыре». Однако, при нахождении ответа, учащиеся все также пересчитывают. При использовании такой словесной формы учащиеся готовятся к выполнению стандартных записей решения с использованием знаков действий. На третьем этапе вводятся математические знаки +, :, = . При помощи этих действий происходит обучение детей записыванию решения задач. В первом классе в полном объеме осуществляется изучение табличных случаев сложения и вычитания однозначных чисел. При этом учащиеся учатся вычислять сложение и вычитание однозначных чисел не только в пределах десяти; каждая часть таблицы сложения (прибавление чисел 2, 3, 4, 5, ...) рассматривается сразу на числовой области 1-20. Программа по математике для первого класса имеет такую структуру, которая позволяет познакомить первоклассников, как можно разными способами выполнять арифметические действия. При этом приоритет отдаётся письменным вычислениям. Что касается устных вычислений, то здесь происходит ознакомление с простыми случаями сложения, вычитания, умножения и деления, с которыми учащиеся могут справиться в уме. Устные приёмы вычислений часто выступают как частные случаи общих правил. Практическая направленность начального курса математики подкрепляется введением в часть арифметики знакомства учеников первого класса с микрокалькулятором, как при его помощи производить арифметические расчёты. Величины распределены в программном содержании так, что формирование соответствующих умений производится в течение продолжительных интервалов времени. Так, в первом классе происходит изучение длины, как одной из величин. И всех известных величин длины первоклассники знакомятся с сантиметром и дециметром, учатся измерять длину предмета при помощи обычной ученической линейки. С ее же помощью первоклассники учатся чертить отрезки заданной длины (в сантиметрах, в дециметрах, в дециметрах и сантиметрах). Программа начального образования предусматривает знакомство младших школьников первого класса с начальными геометрическими понятиями. Дети знакомятся с наиболее распространёнными геометрическими фигурами (круг, многоугольник, отрезок, луч, прямая, куб, шар, конус, цилиндр, пирамида, прямоугольный параллелепипед), учатся находить отличия между ними. Программа направлена на развитие пространственного воображения, о чем говорилось выше, поэтому особое внимание уделяется взаимному расположению фигур на плоскости. Немаловажным также становится обучение первоклассников совершать элементарные графические действия - построение отрезков, ломаных, окружностей, углов, многоугольников, решать на этой основе практические задачи (делить отрезок на две равные части, окружность – на шесть частей и т.п.). 1.2 Понятие предметных моделей Не секрет, что математический язык – это модели, из которых складывается моделирование – математическая речь. И насколько хорошо ребенок овладевает данной речью, проявляется его успешность в обучении математике. Причем здесь речь идет не только об академической успешности. Важно, чтобы ученик был успешен в практической жизни, в умении применять усвоенные математические умения на практике, решая реальные жизненные ситуации. Если снова обратиться к тексту ФГОС НОО, а именно образовательной области «Математика», то среди целей, на которые она направлена, можно увидеть - «формирование предметной математической и ключевых компетентностей, необходимых для самореализации учащихся в быстроизменяющемся мире». Предметная математическая компетентность рассматривается как «личностное образование, которое характеризует способность ученика (ученицы) создавать математические модели процессов окружающего мира, применять опыт математической деятельности во время решения учебно-познавательных и практически ориентированных задач». Таким образом, основной частью обучения математике становится развитие способности применять модели, пользоваться терминологией, установленной в математике, использовать знаки и графические символы. Развитие этих умений становится частью развивающего компонента обучения, а модели, применяемые на уроках – не только наглядностью, но и способом формирования тог самого умения учиться. Моделирование — это одно из средств познания действительности. При помощи моделей можно изучить разнообразные объекты, предметы и явления, решить определенные задачи, получить необходимую информацию. Следовательно, модель - некий объект (система), при помощи которого есть возможность узнать что-то о другом объекте (оригинале). Сущность моделирования можно рассмотреть с двух сторон: во-первых, моделирование выступает в роли содержания, необходимого для усвоения в процессе обучения; во-вторых, моделирование – это учебное действие, без которого обучение в полном объеме не представляется возможным. Модель является наглядной, что говорит о присутствии в ней некой закономерности. Наглядная модель создается на основе той модели, которая возникает в сознании, наглядного образа моделируемого объекта. Иными словами, сначала ребенок воспроизводит мысленный образ, а затем под руководством педагога выстраивает образную наглядную модель. Мысленные модели могут создавать е только дети, но и взрослые, также воспроизводить их на практике в наглядную модель. Дети, воспроизведя мысленный образ в наглядный, могут совершать с ним разные практические действия. В работе с детьми модели служат заменителями предметов: символы и знаки, плоскостные модели (планы, карты, чертежи, схемы, графики), объемные модели, макеты. Моделирование, становясь компонентом образования, помогает решать важные задачи: дает возможность ребенку продуктивно и творчески развиваться; развивает высшие формы образного мышления; дает возможность применить полученные ранее знаний для выполнения практических заданий; способствует закреплению математических знаний, полученных детьми ранее; способствует созданию благоприятных условий для делового сотрудничества; активизирует математическую речь учащихся; способствует развитию мелкой моторики руки; предоставляет возможность овладеть новыми умениями в процессе работы; формирует наиболее глубокое понимание детьми принципов работы и строения оригиналов с помощью моделей. Модель дает нам не просто возможность создать наглядный образ моделируемого объекта, c ее помощью можно узнать, какими свойствами обладает этот образ. Несущественные свойства при этом отбрасываются, и так происходит создание обобщённого наглядного образа моделируемого объекта. С научной точки зрения, центром моделирования является теория аналогии, ключевое понятие которой - понятие аналогии, или, чем похожи объекты по их качественным и количественным характеристикам. Наиболее общим понятием аналогии является абстракция. Аналогия выражает особого рода соответствие между сопоставляемыми объектами, между моделью и оригиналом. У моделирования много функций и использовать его можно ля разнообразных целей и на разных исследовательских этапах. С течение времени появилось большое разнообразие видов, типов, форм моделей. Рассмотрим классификацию, предлагаемую Л. М. Фридманом (рис.1). С точки зрения степени наглядности он все модели разбивает на два класса: 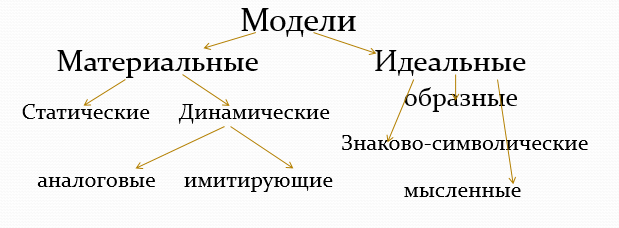 Рис. 2. классификаци моделей Л. М. Фридмана по наглядности Разделить модели в отдельные группы можно, если опираться на определенные их характеристики: 1) по характеру моделей (то есть по средствам моделирования); 2) по характеру моделируемых объектов; 3) по сферам приложения моделирования (моделирование в технике, в физических науках, в химии, моделирование процессов живого, моделирование психики и т. п.) 4) по уровням («глубине») моделирования. Самой распространённой является группа моделей, собранная по их характеру. В этой группе есть конкретные виды: 1. Предметное моделирование. Данное моделирование предполагает воспроизведение функционала того или иного объекта геометрического, динамического характера. Это может быть модель моста, плотины, модель крыла самолета и т.д. 2. Аналоговое моделирование. В таком виде моделирования модель и оригинал описываются единым математическим соотношением. Такой моделью является любая модель, работающая на электричестве. Такие модели применяют для изучения механических, гидродинамических и акустических явлений. 3. Знаковое моделирование. Это моделирование, в котором вместо моделей используются разнообразные знаковые образования: схемы, графики, чертежи, формулы, графы, слова и предложения. 4. Мысленное моделирование. Данный вид моделирования имеет связь со знаковым. Различие лишь в том, то модели воспроизводятся мысленно. 5. Моделированый эксперимент. Данный вид обладает сое особенностью. При нем используется не сам объект, а его модель. Таким образом, моделирование призвано выделять и фиксировать общие закономерности того или иного предмета для последующего его познания. При этом моделирование не просто наглядно показывает тот или иной предмет, а становится стимулом для практической деятельности учащихся. Способность учащихся использовать модели, преобразовывать их для того, чтобы понять общие свойства определенных понятий - одна из главных задач обучения во всех предметных областях. СПИСОК ЛИТЕРАТУРЫ 1.Осмоловская, И. М. Формирование универсальный учебных действий у учащихся начальных классов / И. М. Осмоловская, Л. Н. Петрова // Начальная школа. – 2012 – № 10 – С. 6–12. 2 Федеральный государственный образовательный стандарт начального общего образования (утвержден приказом Минобрнауки России от 22 сентября 2011 г. № 2357) - Электронный ресурс –Режим доступа http://standart.edu.ru/catalog.aspx?CatalogId=959 (дата обращения 30.03.2022) 3.Царева, С. Е. Учебная деятельность и умение учиться в современных условиях / С. Е. Царева // Начальная школа. – 2019 – № 5 – С. 13–17. 4.Примерная основная образовательная программа образовательного учреждения. Начальная школа/ [сост. Е. С. Савинов]. — 4е изд., перераб. — М. : Просвещение, 2013. – 240с. 5.Федеральный государственный образовательный стандарт начального общего образования (утвержден приказом Минобрнауки России от 22 сентября 2011 г. № 2357) - Электронный ресурс –Режим доступа http://standart.edu.ru/catalog.aspx?CatalogId=959 (дата обращения 30.03.2022) |
