Теоретические основы электротехники
 Скачать 366.49 Kb. Скачать 366.49 Kb.
|
L2 L3 I2 I3 L L4 Гн; I I4 A ; L5 I5 L6 L7 I6 I7 Строим график зависимости индуктивности обмотки от величины тока в ней. 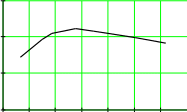 0.03 0.030.02  Гн L 0.01 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 I A Задача 3 Электрическое поле коаксиального кабеля Дан коаксиальный кабель с двухслойной изоляцией, имеющий длину в осевом направлении l 20м. n 4 ; N 6. Удельная проводимость слоев: 1 2 ( 1 0.1 n) 9 10 10 ( 2 0.2 n) 9 ; 1.4 10 9 Смм   1 1 ; 1.4 10 9 Смм Радиус жилы: R1 0.01N м ; R1 0.06 м Радиус граничной поверхности между слоями: R2 0.01N 0.02 м; R2 0.08 м Радиус оболочки: R3 0.01N 0.04 м; R3 0.1 м Оболочка заземлена, напряжение между жилой и оболочкой: U0 6000 В Электрическая постоянная: 0 8.85 10 12 Ф   м мТребуется: Определить сопротивление изоляции кабеля, ток утечки, потери мощности в изоляции, напряжение на каждом слое изоляции. Рассчитать и построить кривые распределения плотности тока; напряженности электрического поля и потенциала в каждом слое изоляции. Решение Составим электрическую схему замещения: I  C1 C1U0 C2 Проводимость: 2 1 l  g ; 1 R2  ln ln g1 6.115 107 См R1 2 2 l  g2 g2 R3  ln ln ; g2 1.577 10 6 См R2 Cопротивление слоев: 1  g r1 1 1  g r2 2 ; r1 1.64 106 Ом ; r2 6.34 105 Ом Эквивалентное сопротивление изоляции кабеля: rэ r1 r2 ; rэ 2.27 106 Ом Эквивалентная проводимость изоляции кабеля: 1  r Yэ э ; Yэ 4.406 10 7 См Ток утечки: I Yэ U0 ; I 0.00264 А Плотность тока проводимости J( r) I  2 l r U1 r1 II1 g1 U1 ; U1 4.323 103 В ; I1 2.644 10 3 А J1( r) I1  2 l r U2 r2 II2 g2 U2 ; U2 1.677 103 В ; I2 2.644 10 3 А J2( r) I2  2 l r Кривая плотности тока проводимости: J( r) J1( r)  J2( r) J2( r)ifR1 r R2ifR2 r R3  4104 4104 3104 3104R1 R3  А/м^2 J(r) 2104   1104 1104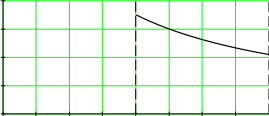 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09r м Кривая распределения напряженности электрического поля: E1( r) E( r) J1( r)  1  E1( r) E1( r)E2( r) E2( r) ifR1 r R2ifR2 r R3 J2( r)  2 3105  R1 R3 R1 R3В/м E(r) 2105  1105 11050.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 r м Потенциал: U E( r) dr U1( r) U2( r) I  2 l 1 I  2 l 2 ln( r) ln( r)  U( r) U( r) I ln r U0 ifR1 r R2   2 l 1 2 l 1I  R1 R2 ln  I ln  r U  ifR r R 2 l 1 R1 2 l 2 R2 0 2 3  В 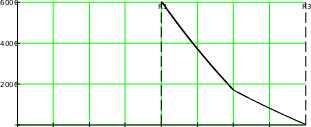 U(r) U(r) 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 r м Задача 6 Магнитное поле цилиндрического проводника По цилиндрическому медному проводу протекает постоянный ток I. В плоскости, проходящей через ось провода, расположена катушка из тонкой проволоки с числом витков w n. 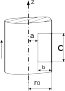 Численные данные: Численные данные:w 4 I N ; I 6 A r0 0.3 0.01 na 0.1 0.01 n ; r0 0.34 м I ; a 0.14 м b 0.2 ; b 0.2 м 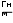 c 0.01 nм ; c 0.04 м c 0.01 nм ; c 0.04 м7 0 4 10 Решение Определить зависимость векторного магнитного потенциала Aв функции от радиуса от оси цилиндра, построить график A(r). Внутри провода при 0 r r0  A1( r) A1( r) В области r0 r 0 I4 r0 r2 2 A( r) 0 I 1 2 ln r   2 Строим график: 4 r0 A( r) A1( r)  A2( r) A2( r)if0 r r0 ifr0 r 4 r0 A*Гн/м A(r) 1106      2106 2106  3106 3106
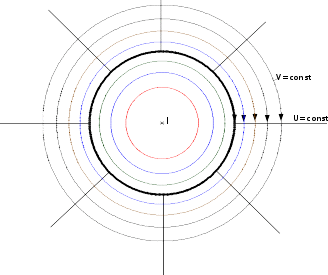
0 0.2 0.4 0.6 0.8 1 1.2 r м Вычислить магнитный поток, замыкающийся в самом проводе на 1м его длины, потокосцепление, самоиндукции и внутреннюю индуктивность. Adl 0 I 4 7 6 7  Ar0 l= =  4 4 4 6 10 Вб Lвнутр 0 l  = =8 4 7 1  10 8 5 10 8Гн Найти выражение взаимной индуктивности M между проводом и рамкой. Вычислить взаимную индуктивность для заданных параметров. Для определения М определим потокосцепление с катушкой, созданное током I в проводе. Индукция внутри провода: 0 I r  B B0 2 r2 Магнитный поток, сцепленный с катушкой, связан с индукцией отношением Bds Поверхность интегрирования s, ограниченную контуром катушки, можно считать плоской. В таком случае угол между B и ds во всех точках поверхности равен нулю, а элемент поверхности можно предстваить в виде полоски длиной си шириной dx. ds c dx Интегрируя получаем: ab Bds 0 I x  cdx cdx0 I   c ( a b) 2 a2 c ( a b) 2 a2 0 I c b2 2a b 2 r02 a 4 r02 4 r02 Находим потокосцепление с катушкой: w 0 I  4 r02 c w b2 2a b  Взаимная индуктивность: M Взаимная индуктивность: M I 0  M M4 r02 c w b2 2a b = 4 7  10 4 0.342 0.04 4 0.22 2 0.14 0.2 1.329 10 8 Гн Найти э.д.с. е(t), индуктируемую в прововоде током i 10 sin( 314t 30)A, протекающем в катушке. e( t) d d 0 I c b2 2a b 0 c b2 2a b d( 10 sin( 314 t 30) )     dt dt dt dt 4 r02 4 r02 dt e( t) 3.322 10 9 0.04 314 cos( 314 t 30) 4.172 10 8 cost 30 В   Построить картину магнитного поля, изобразив трубки магнитной индукции и линии равного скалярного магнитного потенциала. Потоки всех магнитных трубок ( ) как внутри, так и вне провода должны быть одинаковыми. Разности магнитных потенциалов между каждой парой соседних линий равного потенциала должны быть одинаковыми. Построить картину магнитного поля, изобразив трубки магнитной индукции и линии равного скалярного магнитного потенциала. Потоки всех магнитных трубок ( ) как внутри, так и вне провода должны быть одинаковыми. Разности магнитных потенциалов между каждой парой соседних линий равного потенциала должны быть одинаковыми.l 2 r0 l 2.1363м 10 Построение картины начинаем с области внутри провода. Магнитный поток, замыкающийся внутри провода:  i i0 I l4 i 1.282 6 Вб Выберем количество трубок индукции: m 4 i  Поток в одной трубке: i m Поток в одной трубке: i mr02  K K 0.029 K K 0.029m Радиусы линий магнитной индукции, разделяющих магнитный поток на трубки равного магнитного потока: 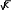 r1 ; r1 0.17 м r1 ; r1 0.17 м r2 ; r2 0.2404 м r2 ; r2 0.2404 м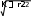 r3 ; r3 0.2944 м r3 ; r3 0.2944 м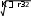 r4 ; r4 0.34 м r4 ; r4 0.34 м Потоки всех магнитных трубок ( ) как внутри, так и вне провода должны быть одинаковыми, тогда Потоки всех магнитных трубок ( ) как внутри, так и вне провода должны быть одинаковыми, тогда e i e 3.204 10 7 Вб Показатель геометрической прогрессии, в соответствии с которой меняются радиусы, ограничивающие внешние трубки индукции:  e2 e2N e 0Il N 1.133 r5 N r0r6 N r5r7 N r6r8 N r7 r5 0.3853мr6 0.4366мr7 0.4947мr8 0.5606м |