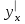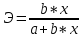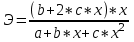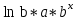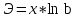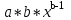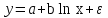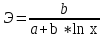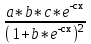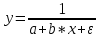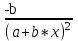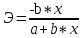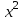Парная регрессия и коррекция. ПАРНАЯ РЕГРЕССИЯ И КОРРЕЛЯЦИЯ. Теоретические сведения
 Скачать 196.62 Kb. Скачать 196.62 Kb.
|
|
ПАРНАЯ РЕГРЕССИЯ И КОРРЕЛЯЦИЯ Теоретические сведенияПарная регрессия – уравнение связи двух переменных y и x: 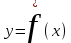 , ,где 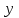 – зависимая переменная (результативный признак), – зависимая переменная (результативный признак), – независимая, объясняющая переменная (признак-фактор). – независимая, объясняющая переменная (признак-фактор).Различают линейные и нелинейные регрессии. Линейная регрессия: 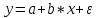 . .Нелинейные регрессии делятся на два класса: регрессии, нелинейные относительно включенных, но линейные по оцениваемым параметрам, и регрессии, нелинейные по оцениваемым параметрам. Регрессии, нелинейные по объясняющим переменным: полиномы разных степеней  ; ;равносторонняя гипербола 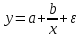 . .Регрессии, нелинейные по оцениваемым параметрам: степенная 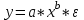 ; ;показательная  ; ;экспоненциальная 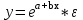 . .Построение уравнения регрессии сводится к оценке ее параметров. Для оценки параметров регрессий, линейных по параметрам, используют метод наименьших квадратов (МНК). МНК позволяет получить такие оценки параметров, при которых сумма квадратов отклонения фактически значений результативного признака  от теоретических от теоретических  минимальна, то есть минимальна, то есть  . .Для линейных и нелинейных уравнений, приводимых к линейным, решается следующая система относительно 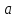 и и 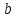 : :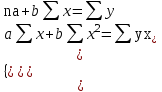 Тесноту связи изучаемых явлений оценивает линейный коэффициент парной корреляции  для линейной регрессии для линейной регрессии  : : , ,и индекс корреляции 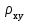 - для нелинейной регрессии - для нелинейной регрессии 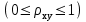  . .Оценку качества построенной модели дает коэффициент (индекс) детерминации, а также средняя ошибка аппроксимации. Средняя ошибка аппроксимации – среднее отклонение расчетных значений от фактических:  . .Допустимый предел значений 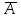 - не более 8 – 10 %. - не более 8 – 10 %.Средний коэффициент эластичности  показывает, на сколько процентов в среднем по совокупности изменяется результат показывает, на сколько процентов в среднем по совокупности изменяется результат 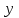 от своей средней величины при изменении фактора от своей средней величины при изменении фактора  на 1 % от своего среднего значения: на 1 % от своего среднего значения: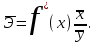 Поскольку коэффициенты эластичности представляют экономический интерес, в таблице приведены формулы расчета коэффициентов эластичности для наиболее распространенных типов уравнений регрессии. Таблица Коэффициенты эластичности для ряда математических функций
Задача дисперсионного анализа состоит в анализе дисперсии зависимой переменной: 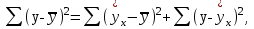 где  - общая сумма квадратов отклонений; - общая сумма квадратов отклонений;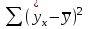 - сумма квадратов отклонений, обусловленная регрессией («объясненная» или «факторная»); - сумма квадратов отклонений, обусловленная регрессией («объясненная» или «факторная»);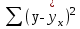 - остаточная сумма квадратов отклонений. - остаточная сумма квадратов отклонений.Долю дисперсии, объясняемую регрессией, в общей дисперсии результативного признака 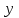 характеризует коэффициент (индекс) детерминации характеризует коэффициент (индекс) детерминации 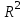 : :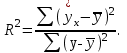 Коэффициент детерминации – квадрат коэффициента или индекса корреляции. 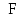 – тест – оценивает качество уравнения регрессии – состоит в проверке гипотезы – тест – оценивает качество уравнения регрессии – состоит в проверке гипотезы 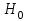 о статистической незначимости уравнения регрессии и показателя тесноты связи. Для этого выполняется сравнение фактического о статистической незначимости уравнения регрессии и показателя тесноты связи. Для этого выполняется сравнение фактического  и критического (табличного) и критического (табличного) 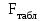 значений значений 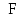 – критерия Фишера. – критерия Фишера.  определяется из соотношения значений факторной и остаточной дисперсий, рассчитанных на одну степень свободы: определяется из соотношения значений факторной и остаточной дисперсий, рассчитанных на одну степень свободы: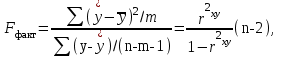 где  - число единиц совокупности; - число единиц совокупности; - число парметров при переменных - число парметров при переменных  . .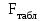 – это максимальное возможное значение критерия под влиянием случайных факторов при данных степенях свободы и уровне значимости – это максимальное возможное значение критерия под влиянием случайных факторов при данных степенях свободы и уровне значимости  . Уровень значимости . Уровень значимости  - вероятность отвергнуть правильную гипотизу при условии, что она верна. Обычно - вероятность отвергнуть правильную гипотизу при условии, что она верна. Обычно  принимается равной 0,05 или 0,01. принимается равной 0,05 или 0,01.Если 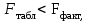 то то 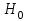 - гипотеза о случайной природе оцениваемых характеристик отклоняется и признается их статистическая значимость и надежность. Если - гипотеза о случайной природе оцениваемых характеристик отклоняется и признается их статистическая значимость и надежность. Если  то гипотиза то гипотиза 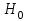 не отклоняется и признается статистическая незначимость, ненадежность уравнения регрессии. не отклоняется и признается статистическая незначимость, ненадежность уравнения регрессии.Для оценки статистической значимости коэффициентов регрессии и корреляции расчитывается  - критерий Стьюдента и доверительные интервалы каждого из показателей. Выдвигается гипотеза - критерий Стьюдента и доверительные интервалы каждого из показателей. Выдвигается гипотеза 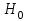 о случайной природе показателей, то есть о незначимом их отличии от нуля. Оценка значимости коэффициентов регрессии и корреляции с помощью о случайной природе показателей, то есть о незначимом их отличии от нуля. Оценка значимости коэффициентов регрессии и корреляции с помощью  - критерия Стьюдента проводится путем сопоставления их значений с величиной случайной ошибки: - критерия Стьюдента проводится путем сопоставления их значений с величиной случайной ошибки:  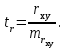 Случайные ошибки параметров линейной регрессии и коэффициента корреляции определяются по формулам:   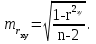 Сравнивая фактическое и критическое (табличное) значение  - статистики - - статистики -  и и  - принимаем или отвергаем гипотезу - принимаем или отвергаем гипотезу 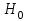 . .Связь между 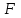 – критерием Фишера и – критерием Фишера и  - статистикой Стьюдента выражается равенством - статистикой Стьюдента выражается равенством Если  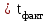 , то , то 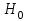 отклоняется, то есть отклоняется, то есть 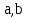 и и  не случайно отличаются от нуля и сформировались под влиянием систематически действующего фактора не случайно отличаются от нуля и сформировались под влиянием систематически действующего фактора  . Если . Если 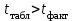 , то гипотеза , то гипотеза 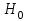 не отклоняется и признается случайная природа формирования не отклоняется и признается случайная природа формирования  и и  . .Для расчета доверительного интервала определяем предельную ошибку  для каждого показателя: для каждого показателя: 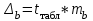 . .Формулы для расчета доверительных интервалов имеют следующий вид  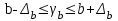 . .Если в границы доверительного интервала попадает ноль, то есть нижняя граница отрицательна, а верхняя положительна, то оцениваемый параметр принимается нулевым, так как он не может одновременно принимать и положительное, и отрицательное значение. Прогнозное значение  определяется путем подстановки в уравнение регрессии определяется путем подстановки в уравнение регрессии 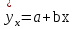 соответствующего (прогнозного) значения соответствующего (прогнозного) значения 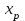 . Вычисляется средняя стандартная ошибка прогноза . Вычисляется средняя стандартная ошибка прогноза  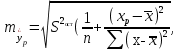 и строится доверительный интервал прогноза:  Пример По группе предприятий, выпускающих один и тот же вид продукции, рассматривается функция издержек:  где 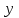 - издержки производства (тыс. д. е.); - издержки производства (тыс. д. е.); - объем выпуска продукции (тыс. ед.). - объем выпуска продукции (тыс. ед.).Исходные данные и вспомогательные вычисления для расчета оценок параметров 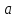 и и 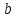 приведены в табл. 1. приведены в табл. 1.Таблица 1
Система нормальных уравнений МНК будет иметь вид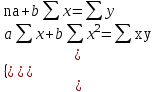 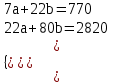 Решая ее, получим:   Тогда, уравнение регрессии  Подставив в уравнение значения х, получим теоретические значения  (последний столбец табл. 1). (последний столбец табл. 1).Коэффициент регрессии 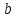 показывает, что при увеличении выпуска продукции на 1 тыс. единиц, затраты на производство по группе предприятий возрастут в среднем на 36,6 тыс. д. е. показывает, что при увеличении выпуска продукции на 1 тыс. единиц, затраты на производство по группе предприятий возрастут в среднем на 36,6 тыс. д. е.То, что  , соответствует опережению изменения результата над изменением фактора. , соответствует опережению изменения результата над изменением фактора.В рассматриваемом примере имеем  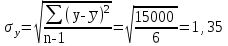 Величина линейного коэффициента корреляции  что достаточно близко к 1 и означает наличие очень тесной зависимости затрат на производство от величины объема выпущенной продукции. Для оценки качества линейной функции рассчитаем коэффициент детерминации  Следовательно, уравнением регрессии объясняется 97,6 % дисперсии результативного признака, а на долю прочих факторов приходится лишь 2,4 % его дисперсии (то есть остаточная дисперсия). Так как 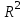 близок к 1, следовательно, линейная модель хорошо аппроксимирует исходные данные и ее можно использовать для прогноза значений результативного признака. близок к 1, следовательно, линейная модель хорошо аппроксимирует исходные данные и ее можно использовать для прогноза значений результативного признака.Для оценки существенности линейной регрессии рассчитаем: Общая сумма квадратов отклонений результативного признака 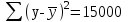 . .Факторная сумма квадратов 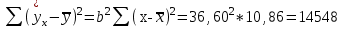 . .Остаточная сумма квадратов 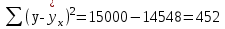 . .Факторная дисперсия 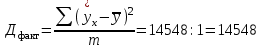 . .Остаточная дисперсия 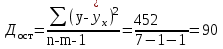 . .F – критерий  Табличное значение 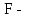 критерия для числа степеней свободы критерия для числа степеней свободы  и уровня значимости и уровня значимости  = 0,05 равно = 0,05 равно 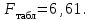 Поскольку  (161,64>6,61), то можно сделать вывод о значимости уравнения регрессии (связь доказана). Оценка значимости уравнения регрессии обычно делается в виде таблицы дисперсного анализа. (161,64>6,61), то можно сделать вывод о значимости уравнения регрессии (связь доказана). Оценка значимости уравнения регрессии обычно делается в виде таблицы дисперсного анализа.Таблица 2 Дисперсный анализ результатов регрессии
Так как в линейной регрессии оценивается значимость не только уравнения в целом, но и отдельных его параметров, рассчитаем по каждому параметру стандартные ошибки: 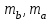 и корреляции и корреляции  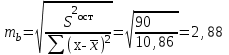 ; ;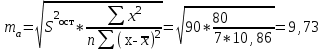 ; ;  . .Фактическое значение 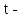 критерия Стьюдента: критерия Стьюдента: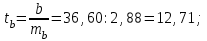  . .Проверим справедливость равенства:  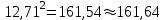 (расхождения за счет округления). При числе степеней свободы 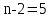 и уровне значимости и уровне значимости  = 0,05 табличное значение = 0,05 табличное значение  Так как  (2,57<12,71), то, следовательно, гипотезу о несущественности коэффициента регрессии можно отклонить. Доверительный интервал для коэффициента регрессии (2,57<12,71), то, следовательно, гипотезу о несущественности коэффициента регрессии можно отклонить. Доверительный интервал для коэффициента регрессии 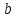 определяется как определяется как  . 95 %-ные границы составят: . 95 %-ные границы составят: ; ; . .Так как  то то 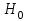 принимаем и считаем параметр принимаем и считаем параметр 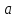 случайно отличным от нуля. случайно отличным от нуля. 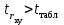 (14,11>2,57), следовательно, коэффициент корреляции существенно отличен от нуля и зависимость является достоверной. (14,11>2,57), следовательно, коэффициент корреляции существенно отличен от нуля и зависимость является достоверной.Для определения интервала прогноза по линейному уравнению регрессии рассчитаем: Точечный прогноз  при прогнозном при прогнозном 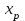 , составляющем 190 % от среднего уровня. , составляющем 190 % от среднего уровня.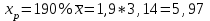 ; ; . .Средняя стандартная ошибка прогноза  . .Для прогнозируемого  95 %-ный доверительный интервал при заданном 95 %-ный доверительный интервал при заданном 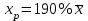 определяется выраженным: определяется выраженным: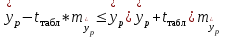 ; ; ; ;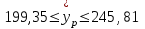 . .Чтобы иметь общее суждение о качестве модели определим среднюю ошибку аппроксимации: 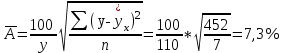 , ,что говорит о хорошем качестве уравнения регрессии, так как ошибка в пределах 5 - 7 % свидетельствует о хорошем подборе модели к исходным данным. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||