теория к экзамену по алгебре 2 семестр 1 курс. Теор.экз.2.2022. Теоретические вопросы к экзамену (2 семестр) по дисциплине Линейная алгебра и аналитическая геометрия
 Скачать 17.02 Kb. Скачать 17.02 Kb.
|
|
Теоретические вопросы к экзамену (2 семестр) по дисциплине «Линейная алгебра и аналитическая геометрия» Данные вопросы или их отдельные части будут присутствовать в экз. билетах, а также могут быть заданы устно экзаменатором. 1. Правило Крамера решения линейной алгебраической системы и его следствия (из 1 семестра). 2. Формулировка критерия совместности (теорема Кронекера-Капелли) линейной алгебраической системы. 3. Формулировка теоремы о структуре общего решения линейной однородной системы. Определение ФСР. 4. Формулировка теоремы о структуре общего решения совместной линейной неоднородной системы. 5. Матрица перехода от одного базиса к другому. Закон преобразования координат вектора при переходе к новому базису. 6. Определения оператора и линейного оператора (далее сокращенно л.о.), обратимого л.о. Матрица л.о. и закон ее преобразования при переходе к новому базису. 7. Определения образа, ядра, ранга, дефекта л.о. Связь ранга и дефекта л.о. 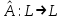 с с 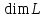 . . Критерий обратимости л.о. в терминах его образа, ядра, ранга, дефекта. 8. Определение собственного вектора и собственного числа л.о. Свойство системы векторов с различными собственными числами. 9. Определение собственного вектора и собственного числа квадратной матрицы. 10. Определение л.о. простого типа. Вид матрицы л.о. простого типа в собственном базисе. Необходимое и достаточное условия простоты л.о. 11. Определения линейной и билинейной функций в линейном пространстве. Их представление линейной и билинейной формами в заданном базисе. Закон преобразования матрицы билинейной формы при переходе к новому базису. 12. Определение квадратичной функции. Ее представление квадратичной формой (далее сокращенно кв.ф.) в заданном базисе. 13. Канонический и нормальный виды кв.ф. Формулировка теоремы Лагранжа о приведении кв.ф. к каноническому виду. Закон инерции кв.ф. Индексы инерции кв.ф. 14. Определения знакопеременной, знакопостоянной и знакоопределенной кв.ф. Исследование на знак кв.ф. по ее индексам инерции. 15. Критерий Сильвестра положительной (отрицательной) определенности кв.ф. 16. Определение евклидова пространства, длины вектора, угла между векторами. Неравенство треугольника, неравенство Коши=Буняковского. 17. Матрица Грама скалярного произведения в заданном базисе евклидова пространства, ее свойства. Закон преобразования матрицы Грама при переходе к новому базису. 19. Ортогональный и ортонормированный базисы евклидова пространства. Метод Грама-Шмидта ортогонализации базиса. 20. Определения сопряженного и самосопряженного л.о. Свойства собственных чисел и собственных векторов самосопряженного л.о. 21. Определения ортогонального преобразования координат и ортогональной матрицы. 22. Формулировка теоремы о приведении кв.ф. к каноническому виду ортогональным преобразованием координат. Канонический вид кв.ф., получаемый приведения ее к каноническому виду ортогональным преобразованием координат. 23. Определение ортогонального л.о. в евклидовом пространстве, его свойства. |
