ззз. хуй (1). Теоретический материал к практическому занятию

• Название: Теоретический материал к практическому занятию
• Дата: 08.09.2022
• Размер: 105.07 Kb.
• Имя файла: хуй (1).docx
• Тип: Документы; #668164
• страница: 3 из 4

Примеры решения задач

1. 
   Две материальные точки движутся согласно уравнениям x
   

 At Bt²  Ct³,

x At Bt²  Ct³, A 4 м/ с, A 2 м/ сB 8 м/ с² , B

 4 м/ с² ,

1 1 1 1

^{2 2 1} 1 2 ^{1 2}

C 16 м/ с³, C 1 м/ с³ .Определить скорости v и v в

м/ св момент времени t =1с.

1 2 1 2

Дано: x At Bt2  Ct3,

1 1 1 1 x At Bt2  Ct3, 2 2 1 A1  4 м/ с, A2  2 м/ с B 8 м / с2 , B 4 м / с2 1 2 C 16 м/ с3, C 1 м/ с3 1 2 t 1c

v1 ?, v2 ?

Решение.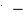
По определению: v  x ^dx

dt

По условию задачи нам известны уравнения движения, из которых найдем скорость, как первую производную от координаты:

v  ^dx1  A 2Bt 3Ct² , v

 ^dx2  A

 2Bt 3Ct².

¹ dt

1 1 1 2 _dt 2 2

1

2
^{v  4  2 81 3}^16^{12  28} ^{м / с}^{, v  2  2  4 1 3112  13} ^{м/ с}^.

Ответ:

v₁  28 м/ с, v₂  13 м/ с.

2. 
   Материальная точка начинает движение вдоль прямой так, что ее ускорение линейно
   

растет и за первые 10 секунд достигает, значения, a 2,5 м/ с².

в конце четвертой секунды. Ответ дать в м/с.

Дано:

а 2,5 м/с 2 .

𝑡1 = 0 𝑐 𝑡2 = 10 𝑐 𝑡 = 4 𝑐

v -?

Решение.
По условию ускорение линейно растет, т.е.

Определить скорость точки

a kt

 k ^a ^{2,5  0}  0,25 м/с³ .

t 10  0

Тогда закон изменения ускорения:

a 0,25t^.

По определению ускорение: a ^dv

dt

 dv  0, 25t dt.

Проинтегрируем обе части уравнения

v 4

_ dv=_ 0, 25tdt,

0 0

получим

4

v  0, 25_ tdt 0, 25 

0

4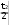

^{ 2}  ^{м/ с}^.

0

Ответ: 2 м/ с.

3. 
   Поезд движется прямолинейно со скоростью
   

v₀  27 м/с . Внезапно на пути возникает

0
препятствие, и машинист, включает тормозной механизм. С этого момента скорость поезда

меняется по закону Ответ дать в метрах.

v  v  kt² , где

k 0,027 м/с³ . Определить тормозной путь поезда.

Дано:

v0  27 м/с

v  v  kt 2 0 k 0,027 м/с3

l-?

Решение.
По определению

_{v } dl

dt

 dl vdt _v₀

• 
  kt² _dt.
  


^t kt³

l _v

0

• 
  kt² dt v t ,
  

0 0
3

так как поезд останавливается, то v
кон

 0 .

0
Из закона изменения скорости определим время торможения: 0  v  kt²,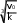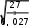

0, 027 10³

Тогда

^{t   10} ^c <sup>, а

l 27 10   261</sup>  ^м^.

3

Ответ: l= 261 м.

4. 
   Движение тела массой 30 кг задано уравнением
   

^x^t ^{ 4t3  2t2 . Определить}

равнодействующую сил, действующих на тело в момент времени 2 с.

Дано:

m=30 кг

𝑥(𝑡) = 4𝑡3 + 2𝑡2 𝑡=2𝑐

F-?

Решение:
По второму закону Ньютона равнодействующая сил равна F  ma , где ускорение определяется как вторая производная от перемещения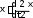

d


dt
a  _12t²  4t_  _24  t 4_ м / с² _.

Для времени t= 2 c

a 24  2  4  52 _ м/ с² _.

Таким образом

^{F ma 30  52  1560} ^Н^.

Ответ:

F 1560Н.

5. 
   Снаряд массой m= 10 кг выпущен из зенитного орудия вертикально вверх со ^{скоростью V}0 ^{= 800 м/c. Считая силу сопротивления воздуха пропорциональной скорости,} определить время tподъёма снаряда (в секундах) до высшей точки. Коэффициент сопротивления k = 0,25 кг/с. Ускорение свободного падения принять 9,8 м/с². Ответ округлите до десятых.
   

Дано:

m = 10 кг V0= 800 м/c k= 0,25 кг/с. Fс kv

t - ?

Решение:

1. 
   делаем рисунок, расставим силы. На снаряд действуют две силы: сила тяжести и сила сопротивления.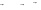
   
2. 
   По второму закону Ньютона:
   

ma  mg  F_c

3. 
   Запишем 2 закон Ньютона в проекциях на ось 0у:
   

(1)

0 y:

mg F_c ma.

(2)
Рис.1.2

4. 
   По условию F_с
   

kv , перепишем (2) в виде

mg kv  m^dv .

dt

(3)

Получилось дифференциальное уравнение движения, чтобы найти время из (3) надо разделить переменные и проинтегрировать.

5. 
   После разделения переменных, получим:
   

dv mg kv

_ dt

m

. (4)

6. 
   Интегральное уравнение выглядит как
   

^{tdt 0 dv} t

0 v
^ m^{ } mg kv

(5) . Левый интеграл равен .

m

Интегрирование правой части проведем заменой переменных.

⁰ dv

mg kv  z,

1 ⁰ dz 1

^v 1 mg kv

7. 
   
   v
   ^ mg kv ^ dz kdv, dv  dz/ k
   

  _


k

z
v

 ln z

k ₀

 ln .

k mg

Приравняем левую и правую части уравнения (5) после интегрирования

t_ 1 _ln mg kv _.

m k mg

Из последнего равенства следует t ^mln ^{mg kv} .

k mg

^{Подставляя числовые значения, получаем} t 44,5c.

Ответ:t=44,5 c.

6. 
   Определить скорость, с которой должен лететь самолет, чтобы при выполнении фигуры «мертвая петля» радиусом 1 км в верхней точке траектории полета летчик находился
   

в состоянии невесомости. Ускорение свободного падения

g 10 м/с² .