ззз. хуй (1). Теоретический материал к практическому занятию
 Скачать 105.07 Kb. Скачать 105.07 Kb.
|
Методические материалыПри решении задач используют два основных способа: аналитический (численный) и графический. Сущность аналитического способа решения задач состоит в использовании законов физики, их математической интерпретации (формул одной или нескольких), составлении системы уравнений и применении правил математики для их целенаправленного преобразования. Графическими задачами называют задачи, в которых объектом исследования являются графики зависимости между физическими величинами, по которым необходимо установить количественные соотношения между физическими величинами, либо установить физические явления и выявить зависимости посредством формул. Задачи кинематики можно разделить на три группы. К первой группе относятся задачи, в которых материальная точка движется прямолинейно, т.е. траектория движения есть прямая линия, в качестве которой удобно использовать одну из координатных осей. Чаще распространены задачи с горизонтальным движением тела, а также различные типы задач о свободном движении по вертикали. При решении задач этой группы используется аналитический метод. Алгоритм решения таких задач можно свести к следующему: Провести анализ условия задачи и определить характер движения материальной точки. Сделать чертеж. Записать уравнение движения материальной точки в векторной форме. Перейти от векторной записи к скалярной, для чего удобнее выбрать декартовую систему координат. Оси лежат в плоскости, в которой движется точка. Обычно начало координат совмещают с положением точки в начальный момент времени, т.е. полагают 𝑥0 = 0, 𝑦0 = 0 при 𝑡 = 0. Проецируя все векторы, входящие в уравнение движения на оси координат, и учитывая, что проекция суммы векторов равна сумме их проекций, перейти от векторных уравнений к скалярным уравнениям. Знаки всех проекций определяются правилом, если вектор образует с направлением оси проекций острый угол, то проекция положительна, если тупой – проекция отрицательна. Воспользоваться дополнительными данными задачи. Далее решаете полученную систему уравнений. Ко второй группе относятся задачи, в которых материальная точка движется криволинейно, например, в случае свободного движения тела, брошенного под углом к горизонту. Используя принцип независимости механических движений, криволинейное движение можно рассматривать как суперпозицию двух независимых одновременных прямолинейных движений вдоль координатных осей. Третью группу составляют прямая и обратная задачи кинематики. Прямая задача заключается в определении кинематических величин по заданному уравнению движения путем дифференцирования радиус-вектора по времени для определения скорости иди дифференцирования мгновенной скорости по времени для нахождения ускорения. Обратная задачи кинематики сводится к определению скорости и уравнения движения по заданному ускорению. В этом случае, кроме зависимости at , необходимо знать начальные условия: скорость и радиус-вектор точки в начальный момент времени 𝑡 = 0. Сначала определяется скорость, путем интегрирования зависимости at . v t at dt C1 , а затем радиус-вектор путем интегрирования скорости: rt v tdt C2 . Значения постоянных интегрирования 𝐶1 и 𝐶2 определяются из физических соображений с учетом начальных условий задачи. В основной задаче динамики по заданным силам и начальным условиям определяют механическое состояние системы. При решении основной задачи динамики возможны два способа задания сил, действующих на материальную точку: силы постоянны по модулю и направлению; сила является переменной величиной, т.е. изменяется со временем. В первом случае возможны варианты движения тел в инерциальных и неинерциальных системах отсчета. При решении задач на движение тел в инерциальных системах отсчета условно можно выделить задачи на движение тел при отсутствии сил трения и задачи на движение тел при наличии сил трения. Более детальная классификация задач сводится к задачам на движение: а) по горизонтальной поверхности; б) по вертикальной поверхности; в) по наклонной плоскости; г) движение материальной точки по окружности. Во многих задачах по динамике поступательного движения можно пренебречь силами трения, возникающими при движении тел и считать, что тела движутся лишь под действием силы тяжести и упругих сил реакции связей (давление опоры, натяжения нитей). Если в задаче рассматривается движение системы связанных между собой тел, то уравнения движения записываются для каждого тела в отдельности. Если тела связаны нитью, массой которой можно пренебречь, то силу натяжения нитей считают одинаковой по всей длине нити. При наличии неподвижного блока сила натяжения нитей одинакова по обе стороны блока, если массой нити и блока, а также силами трения, возникающими при вращении блока, можно пренебречь. Во всех реальных случаях при непосредственном взаимодействии тел возникают силы трения. При решении задач на движение тел при наличии сил трения, составляя уравнение движения, необходимо учитывать силы трения. При этом следует иметь в виду, что сила трения скольжения всегда направлена в сторону, противоположную направлению относительной скорости тела. Указанные типы задач можно решать по следующему алгоритму: Сделать чертеж. Выяснить, какие силы действуют на каждое движущееся тело со стороны других тел, и изобразить эти силы на чертеже. Записать уравнения движения для каждого тела в векторной форме, используя второй закон Ньютона. Чтобы правильно определить направление сил, действующих на движущееся тело, необходимо помнить, что сила тяжести не зависит от условий движения и всегда направлена вертикально вниз; сила реакции опоры всегда перпендикулярна плоскости, на которую опирается тело, и направлена по нормали к соприкасающимся поверхностям в точке их касания в сторону тела; сила натяжения нити направлена вдоль нити в сторону подвеса; сила трения скольжения – в сторону, противоположную скорости тела. Выбрать систему координат. Координатные оси направляют так, чтобы проекции сил на них наглядно выражались. Чаще всего ось 0х направляют по направлению вектора скорости, ось 0у – по направлению, перпендикулярному к вектору скорости. Положительное направление осей удобно указывать так, чтобы оно совпадало с направлением ускорения тела. Для каждого тела можно выбрать свои координатные оси. Найти проекции векторов сил на выбранные системы координат и получить систему алгебраических уравнений с учетом знака проекций сил и ускорений, т.е. записать второй закон Ньютона в виде двух скалярных уравнений. Решить систему уравнений с учетом дополнительных условий из задачи. В случае движения материальной точки по окружности в проекциях на касательную и нормаль к траектории в данной точке уравнения движения принимают вид: dv v2 mdt F , mR Fn, 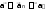 составляющая силы F . Направление орта τ выбирают в сторону возрастания дуговой координаты, а направление орта n – к центру кривизны траектории в данной точке. составляющая силы F . Направление орта τ выбирают в сторону возрастания дуговой координаты, а направление орта n – к центру кривизны траектории в данной точке.При криволинейном движении полное ускорение равно , а его модуль 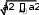 определяется формулой a . определяется формулой a .Для отыскания модуля и направления равнодействующей сил, приложенных к материальной точке необходимо: путем дифференцирования заданного уравнения движения находят скорость точки, а повторное дифференцирование полученных уравнений позволяет найти ускорение, а затем с помощью второго закона Ньютона определяется сила, действующая на материальную точку. |
