алгоритм дейкстры нахождения кратчайшего пути в графе. МонгушББ_КТСО04-20. Теоретический обзор Нейронной сети Хопфилда
 Скачать 166.67 Kb. Скачать 166.67 Kb.
|
|
Оглавление Введение 1.1Теоретический обзор Нейронной сети Хопфилда 1.2 Архитектура Сети 1.3 Обучение сети 1.4 Синхронный Асинхронный режим работы сети 2.1 Построение и реализация нейронной сети Хопфилда Заключение Список использованных литератур Введение Среди различных конфигураций искусственных нейронных сетей встречаются такие, при классификации которых по принципу обучения, которым не подходят ни обучение с учителем, ни обучение без учителя. В таких сетях весовые коэффициенты синапсов рассчитываются только однажды перед началом функционирования сети на основе информации об обрабатываемых данных, и все обучение сети сводится именно к этому расчету. С одной стороны, предъявление априорной информации можно расценивать, как помощь учителя, но с другой - сеть фактически просто запоминает образцы до того, как на ее вход поступают реальные данные, и не может изменять свое поведение, поэтому говорить о звене обратной связи с "миром" (учителем) не приходится. Из сетей с подобной логикой работы наиболее известны сеть Хопфилда. Уже сегодня искусственные нейронные сети используются во многих областях, но прежде чем их можно будет применять там, где на карту поставлены человеческие жизни или значительные материальные ресурсы, должны быть решены важные вопросы, касающиеся надежности их работы. Поэтому уровень допустимых ошибок следует определять исходя из природы самой задачи. Некоторые проблемы с анализом вопросов надежности возникают из-за допущения полной безошибочности компьютеров, тогда как искусственные нейронные сети могут быть неточны даже при их правильном функционировании. На самом же деле компьютеры, как и люди, тоже могут ошибаться. Нейросетевые прикладные пакеты, разрабатываемые рядом компаний, позволяют пользователям работать с разными видами нейронных сетей и с различными способами их обучения. Они могут быть как специализированными (например, для предсказания курса акций), так и достаточно универсальными. Области применения нейронных сетей весьма разнообразны — это распознавание текста и речи, семантический поиск, экспертные системы и системы поддержки принятия решений, предсказание курсов акций, системы безопасности, анализ текстов. В данной курсовой работе рассматривается несколько особенно ярких и интересных примеров использования нейронных сетей в разных областях 1.1 Теоретический обзор Нейронной сети Хопфилда В настоящее время во многих сферах деятельности человека (например, в медицине, в экономике и бизнесе, авиации, в связи, в автоматизации производства, вводе и обработке информации, в охранных системах и т.д.) активно применяются различные искусственные нейронные сети (ИНС). Целью данной работы является всестороннее рассмотрение искусственной нейронной сети Хопфилда. Нейронная сеть Хопфилда – однослойная сеть, в которой каждый нейрон имеет связи со всеми другими нейронами. Сети Хопфилда имеют обратные связи и являются динамическими (рекуррентными), поскольку после получения каждого нового входного сигнала начинается переходный процесс, который заканчивается установлением постоянного выхода или продолжается бесконечно долго. Поэтому проблема устойчивости сети с обратными связями может иметь большое значение при решении прикладных задач. При подаче на вход устойчивой сети нового входного вектора ИНС переходит от состояния к состоянию, пока не стабилизируется. При подаче на вход сети частично неправильного входного вектора сеть стабилизируется в состоянии, ближайшем к желаемому. Для этого веса сети следует выбирать так, чтобы образовывать состояния устойчивого равновесия для каждого входного образа. Каждый нейрон сети Хопфилда получает входной сигнал, а также сигналы с выходов всех остальных нейронов показан на рис 1. 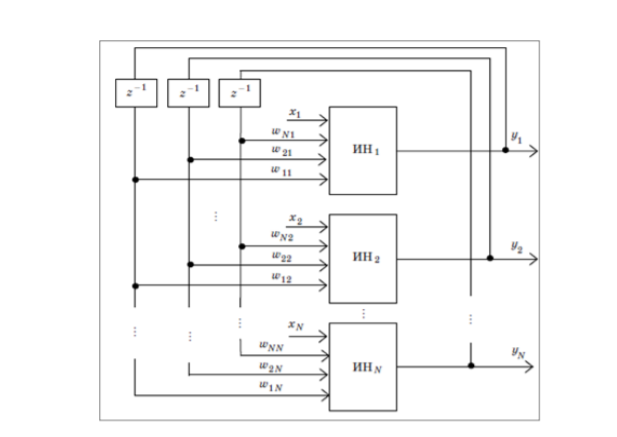 Рис 1. Структура Сети Хопфилда Выход нейрона изменяется по формуле:  Формула 1. где xi – входной сигнал. В качестве активационной используется пороговая функция с порогом Т:  Формула 2. 1.2 Архитектура Сети Архитектуры нейронной сети будети Хопфилда. Данная модель, видимо, является наиболее распространенной математической моделью в нейронауке. Это обусловлено ее простотой и наглядность. Сеть Хопфилда показывает, каким образом может быть организована память в сети из элементов, которые не являются очень надежными. Экспериментальные данные показывают, что при увеличении количества вышедших из строя нейронов до 50%, вероятность правильного ответа крайне близка к 100%. Даже поверхностное сопоставление нейронной сети (например, мозга) и Фон-Неймановской ЭВМ показывает, насколько сильно различаются эти объекты: к примеру, частота изменения состояний нейронов («тактовая частота») не превышает 200Гц, тогда как частота изменения состояния элементов современного процессора может достигать нескольких ГГц (10^9Гц). Формальное описание сети Хопфилда Сеть состоит из N искусственных нейронов, аксон каждого нейрона связан с дендритами остальных нейронов, образуя обратую связь. Архитектура сети изображена на рис. 2. 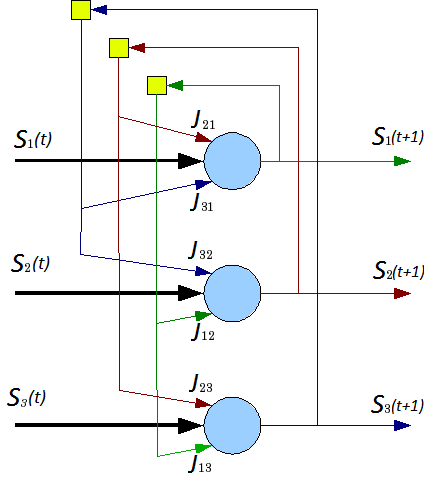 Рис 2. Архитектура сети Каждый нейрон может находиться в одном из 2-х состояний: S (t)  {-1; +1} {-1; +1}где S(t) — состояние нейрона в момент t. «Возбуждению» нейрона соответствует +1, а «торможению» -1. Дискретность состояний нейрона отражает нелинейный, пороговый характер его функционирования и известный в нейрофизиологи как принцип «все или ничего». Динамика состояния во времени i-ого нейрона в сети из N нейронов описывается дискретной динамической системой: 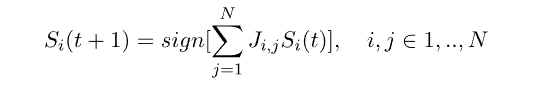 Формула 3. где J_{i,j} — матрица весовых коэффициентов, описывающих взаимодействие дендритов i-ого нейрона с аксонами j-ого нейрона. Стоит отметить, что  Формула 4. 1.3 Обучение сети Алгоритм обучения сети Хопфилда существенно отличается от таких классических алгоритмов обучения перцептронов, как метод коррекции ошибки или метод обратного распространения ошибки. Отличие заключается в том, что вместо последовательного приближения к нужному состоянию с вычислением ошибок, все коэффициенты матрицы рассчитываются по одной формуле, за один цикл, после чего сеть сразу готова к работе. Вычисление коэффициентов основано на следующем правиле: для всех запомненных образов Xi матрица связи должна удовлетворять уравнению: X_i^T=WX_i поскольку именно при этом условии состояния сети Xi будут устойчивы — попав в такое состояние, сеть в нём и останется. Некоторые авторы относят сеть Хопфилда к обучению без учителя. Но это неверно, так как обучение без учителя предполагает отсутствие информации о том, к каким классам нужно относить стимулы. Для сети Хопфилда без этой информации нельзя настроить весовые коэффициенты, поэтому здесь можно говорить лишь о том, что такую сеть можно отнести к классу оптимизирующих сетей (фильтров). Отличительной особенностью фильтров является то, что матрица весовых коэффициентов настраивается детерминированным алгоритмом раз и навсегда, и затем весовые коэффициенты больше не изменяются. Это может быть удобно для физического воплощения такого устройства, так как на схемотехническом уровне реализовать устройство с переменными весовыми коэффициентами на порядок сложнее. Примером фильтра без обратных связей может служить алгоритм CC4 (Cornel classification), автором которого является S.Kak. В сети Хопфилда есть обратные связи и поэтому нужно решать проблему устойчивости. Веса между нейронами в сети Хопфилда могут рассматриваться в виде матрицы взаимодействий W. В работе Cohen, Grossberg[1] показано, что сеть с обратными связями является устойчивой, если её матрица симметрична и имеет нули на главной диагонали. Имеется много устойчивых систем, например, все сети прямого распространения, а также современные рекуррентные сети Джордана и Элмана, для которых не обязательно выполнять условие на симметрию. Но это происходит вследствие того, что на обратные связи наложены другие ограничения. В случае сети Хопфилда условие симметричности является необходимым, но не достаточным, в том смысле, что на достижение устойчивого состояния влияет ещё и режим работы сети. Ниже будет показано, что только асинхронный режим работы сети гарантирует достижение устойчивого состояния сети, в синхронном случае возможно бесконечное переключение между двумя разными состояниями (такая ситуация называется динамическим аттрактором, в то время как устойчивое состояние принято называть статическим аттрактором). Запоминаемые векторы должны иметь бинарный вид. После этого происходит расчёт весовых коэффициентов по следующей формуле:  Формула 4. где N — размерность векторов, m — число запоминаемых выходных векторов, d — номер запоминаемого выходного вектора, Xij — i-я компонента запоминаемого выходного j-го вектора. Это выражение может стать более ясным, если заметить, что весовая матрица W может быть найдена вычислением внешнего произведения каждого запоминаемого вектора с самим собой и суммированием матриц, полученных таким образом. Это может быть записано в виде: 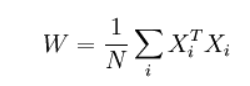 Формула 5. где Xi — i-й запоминаемый вектор-строка. Расчёт этих весовых коэффициентов и называется обучением сети. Как только веса заданы, сеть может быть использована для получения запомненного выходного вектора по данному входному вектору, который может быть частично неправильным или неполным. Для этого выходам сети сначала придают значения этого начального вектора. Затем сеть последовательно меняет свои состояния согласно формуле:  Формула 6. где F — активационная функция, Xi и Xi + 1 — текущее и следующее состояния сети, до тех пор, пока состояния Xi и Xi + 1 не совпадут (или, в случае синхронного режима работы, не совпадут состояния Xi − 1 с Xi + 1 и одновременно Xi − 2 с Xi). Именно этот процесс называется конвергенцией сети. Полученное устойчивое состояние Xi (статический аттрактор), или, возможно, в синхронном случае пара {Xi,Xi + 1} (динамический аттрактор), является ответом сети на данный входной образ. 1.4 Синхронный Асинхронный режим работы сети Если работа сети моделируется на одном процессоре, то при синхронном режиме последовательно просматриваются нейроны, однако их состояния запоминаются отдельно и не меняются до тех пор, пока не будут пройдены все нейроны сети. Когда все нейроны просмотрены, их состояния одновременно (то есть синхронно, отсюда и название) меняются на новые. Таким образом, достигается моделирование параллельной работы последовательным алгоритмом. При реально параллельном моделировании, этот режим фактически означает, что время передачи τij для каждой связи между элементами ui и uj одинаково для каждой связи, что приводит к параллельной работе всех связей, они одновременно меняют свои состояния, основываясь только на предыдущем моменте времени. Наличие таких синхронных тактов, которые можно легко выделить и приводит к пониманию синхронного режима. При синхронном режиме возможно (хотя и далеко не всегда наблюдается) бесконечное чередование двух состояний с разной энергией — так называемый динамический аттрактор. Поэтому синхронный режим практически для сети Хопфилда не используется, и рассматривается лишь как основа для понимания более сложного асинхронного режима. Асинхронный режим работы сети Если моделировать работу сети как последовательный алгоритм, то в асинхронном режиме работы состояния нейронов в следующий момент времени меняются последовательно: вычисляется локальное поле для первого нейрона в момент t, определяется его реакция, и нейрон устанавливается в новое состояние (которое соответствует его выходу в момент t + 1), потом вычисляется локальное поле для второго нейрона с учётом нового состояния первого, меняется состояние второго нейрона, и так далее — состояние каждого следующего нейрона вычисляется с учетом всех изменений состояний рассмотренных ранее нейронов. По сути при последовательной реализации сети Хопфилда явно не видно, в чём заключается асинхронность, но это видно, если сеть Хопфилда реализовать с параллельными вычислениями. В этом случае асинхронный режим сети Хопфилда упрощен, и носит частный случай по сравнению с общим видом асинхронных сетей, где время передачи τij для каждой связи между элементами ui и uj своё, но постоянное. Чтобы рассмотреть работу сети при параллельной реализации, необходимо ввести понятие такта — как минимальное время, за которое происходит передача сигнала по связи, то есть при τij = 1. Тогда за промежуток времени между t и t + 1 происходит определённое количество тактов N. И именно в пределах времени из N тактов происходит асинхроность протекания сигналов и выполнения расчётов. То есть, например, когда нужно рассчитать состояние нейрона №3, необходимо рассчитать состояние нейрона №1 и состояние нейрона №2 и умножить это на соответствующие веса w13 и w23. Но, как оказывается, чтобы рассчитать состояние нейрона №2, нужно знать обновлённое состояние нейрона №1 и старое состояние нейрона №3, умножить их на веса w12 и w32. Понятно, что физически невозможно рассчитать состояние нейрона №1 и состояние нейрона №2 за одно и то же время, так как состояние нейрона №2 зависит от состояния нейрона №1. Поэтому связь между нейроном №1 и нейроном №3 имеет время передачи τij = 2, и достигает нейрона №3 за два такта. Именное такое разное время передачи τij и позволяет говорить о сети Хопфилда как о сети с асинхронным режимом. В асинхронном режиме невозможен динамический аттрактор: вне зависимости от количества запомненных образов и начального состояния сеть непременно придёт к устойчивому состоянию (статическому аттрактору). 2.1 Построение и реализация нейронной сети Хопфилда Реализация нейронной сети Хопфилда, определенной выше будет производиться на языке C++. Для упрощения экспериментов, добавим основные определения типов, напрямую связанных с видом нейрона и его передаточной функции в класс simple_neuron, а производные определим далее. Самыми основными типами, напрямую связанными с нейроном являются: тип весовых коэффициентов (выбран float); тип, описывающий состояния нейрона (введен перечислимый тип с 2 допустимыми значениями). На основе этих типов можно ввести остальные базовые типы: тип, описывающий состояние сети в момент t (выбран стандартный контейнер vector); тип, описывающий матрицу весовых коэффициентов связей нейронов (выбран контейнер vector контейнеров vector).   Листинг 1, Определение новых типов: Листинг 1, Определение новых типов:struct simple_neuron { enum state {LOWER_STATE=-1, UPPER_STATE=1}; typedef float coeff_t; <<(1) typedef state state_t; <<(2) ... }; typedef simple_neuron neuron_t; typedef neuron_t::state_t state_t; typedef vector<state_t> neurons_line; <<(3) typedef vector<vector<neuron_t::coeff_t>> link_coeffs; <<(4) Обучение сети, или, вычисление элементов матрицы J_{i,j}=J_{j,i} в соответствии с (3) производится функцией learn_neuro_net, принимающей на вход список обучающих образов и возвращающей объект типа link_coeffs_t. Значения J_{i,j} вычисляются только для нижнетреугольных элементов. Значения верхнетреугольных элементов вычисляются в соответствии с (4). Общий вид метода learn_neuro_net показан в листинге 2. Листинг 2. Обучение нейронной сети:  link_coeffs learn_neuro_net(const list link_coeffs result_coeffs; size_t neurons_count = src_images.front().size(); result_coeffs.resize(neurons_count); for (size_t i = 0; i < neurons_count; ++i) { result_coeffs[i].resize(neurons_count, 0); } for (size_t i = 0; i < neurons_count; ++i) { for (size_t j = 0; j < i; ++j) { neuron_t::coeff_t val = 0; val = std::accumulate( begin(src_images), end(src_images), neuron_t::coeff_t(0.0), [i, j] (neuron_t::coeff_t old_val, const neurons_line &image) -> neuron_t::coeff_t{ return old_val + (image[i] * image[j]); }); result_coeffs[i][j] = val; result_coeffs[j][i] = val; } } return result_coeffs; } Обновление состояний нейронов реализовано с помощью функтора neuro_net_system. Аргументом метода _do функтора является начальное состояние S_{i}(0), являющееся распознаваемых образом (в соответствии с (5)) — ссылка на объект типа neurons_line. Метод функтора модифицирует передаваемый объект типа neurons_line до состояния нейронной сети в момент времени T. Значение жестко не фиксировано и определяется выражением:  т.е., когда состояние каждого нейрона не изменилось за 1 «такт» Для вычисления (2) применены 2 алгоритма STL: std::inner_product для вычисления суммы произведений весовых коэффициентов и состояний нейронов (т.е. вычисление (2) для определенного i); std::transform для вычисления новых значений для каждого нейрона (т.е. вычисление пункта выше для каждого возможного i) Исходный код функтора neurons_net_system и метода calculate класса simple_neuron показан в листинге 3.  struct simple_neuron { struct simple_neuron {... template <typename _Iv, typename _Ic> static state_t calculate(_Iv val_b, _Iv val_e, _Ic coeff_b) { auto value = std::inner_product( val_b, val_e, coeff_b, coeff_t(0) ); return value > 0 ? UPPER_STATE : LOWER_STATE; } }; struct neuro_net_system { const link_coeffs &_coeffs; neuro_net_system(const link_coeffs &coeffs): _coeffs(coeffs) {} bool do_step(neurons_line& line) { bool value_changed = false; neurons_line old_values(begin(line), end(line)); link_coeffs::const_iterator it_coeffs = begin(_coeffs); std::transform( begin(line), end(line), begin(line), [&old_values, &it_coeffs, &value_changed] (state_t old_value) -> state_t { auto new_value = neuron_t::calculate( begin(old_values), end(old_values), begin(*it_coeffs++) ); value_changed = (new_value != old_value) || value_changed; return new_value; }); return value_changed; } size_t _do(neurons_line& line) { bool need_continue = true; size_t steps_done = 0; while (need_continue) { need_continue = do_step(line); ++steps_done; } return steps_done; } }; Для вывода в консоль входных и выходных образов создан тип neurons_line_print_descriptor, который хранит ссылку на образ и формат форматирования (ширину и высоту прямоугольника, в который будет вписан образ). Для этого типа переопределен оператор <<. Исходный код типа neurons_line_print_descriptor и оператора вывода в поток показан в листинге 4.  Листинг 4. Вывод в поток состояния нейронной сети: Листинг 4. Вывод в поток состояния нейронной сети:struct neurons_line_print_descriptor { const neurons_line &_line; const size_t _width; const size_t _height; neurons_line_print_descriptor ( const neurons_line &line, size_t width, size_t height ): _line(line), _width(width), _height(height) {} }; template <typename Ch, typename Tr> std::basic_ostream operator << (std::basic_ostream neurons_line::const_iterator it = begin(line._line), it_end = end(line._line); for (size_t i = 0; i < line._height; ++i) { for (size_t j = 0; j < line._width; ++j) { stm << neuron_t::write(*it); ++it; } stm << endl; } return stm; } Результат работы нейронной сети, для проверки работоспособности реализации, нейронная сеть была обучена 2 ключевым образам:   Рис 3. Ключевые Образы. На вход подавались искаженные образы. Нейронная сеть корректно распознала исходные образы. Искаженные образы и распознанные образы показаны на рис.4, 5:   Рис.4 Распознавание образа 1.   Рис.5 Распознавание образа 2. Заключение В данной работе посвященной «Нейронной сети Хопфилда» в ходе и результате работы был спроектирован, реализован и протестирован алгоритм, позволяющий распознать исходные данные. Во время выполнения данной работы были успешно завершены следующие задачи: Изучены виды нейронных сетей и их применение. Изучены строение нейронной сети и алгоритм свертки Реализован алгоритм распознающий исходные данные Как мощный механизм обучения нейронные сети могут широко применяться в различных областях. Существует, однако, возможность недоразумений в оценке методик машинного обучения. Они никогда не смогут полностью заменить людей в процессе решения задачи. Нейронные сети должны использоваться для обобщения данных, а не для определения, атрибуты и критерии которого весьма важны при сборе данных. Нейронные сети адаптивны по своей природе, они могут подражать решению проблемы человеком, но они не сообщат нам, какой из критериев решения задачи должен быть принят во внимание перед сбором данных. Кроме того, обучающиеся машины часто используются при формализации знаний из данных реального мира, но сами обучающиеся машины не могут генерировать принципы формализации. Список использованных литератур https://habr.com/ru/post/301406/ https://core.ac.uk/download/pdf/84593658.pdf https://wreferat.baza-referat.ru/Нейронная_сеть_Хопфилда Г.Г. Малинецкий. Математические основы синергетики. Москва, URSS, 2009 https://ru.wikipedia.org/wiki/Нейронная_сеть_Хопфилда https://dspace.tltsu.ru/bitstream/123456789/12678/1/Борисов%20A.A._MOп-1601a.pdf |
