Теоретическое введение
 Скачать 0.63 Mb. Скачать 0.63 Mb.
|
|
Задача 19. Давление морской воды в трубке Пито составляет 39 кПа, а в трубке статического давления 20 кПа. Определить гидродинамический коэффициент лага, если его индикатор показывает скорость 12 узлов. Теоретическое введение. Принцип действия гидродинамического лага основан на измерении гидродинамического давления, создаваемого скоростным напором набегающего потока воды при движении судна. Для измерения этого давления на днище судна устанавливают приемное устройство с двумя каналами (рис. 1), приемные отверстия которых вынесены за пределы пограничного слоя, и одно из них (приемное отверстие трубки Пито) направлено к носу судна. Вследствие возникающего при движении судна скоростного набора набегающего потока воды высота столба h1 в трубке Пито будет больше, чем высота h2 в другой трубке. На основании уравнения Бернулли можно записать, что: h1 = V2/(2g) + Pст/γ (1.1) где V – скорость установившегося ламинарного потока (относительная скорость судна); g – ускорение силы тяжести; Pст – статическое давление воды на уровне входного отверстия трубки Пито; γ – удельный вес воды. Высота столба h2 не зависит от скорости потока и определяется следующим выражением: h2 = Pст/γ (1.2) Тогда: Δh = h1 – h2 = V2/(2g) (1.3) Переходя к величинам давлений можно записать, что: Рд = Рп – Рст = γΔh = ρV2/2 (1.4) где Рд – гидродинамическое давление; Рп – полное давление; ρ = γ/g – плотность воды. Относительную скорость судна вычисляют следующим образом: V = √2Pд/ρ (1.5) Рисунок 1 – Принцип действия гидродинамического лага 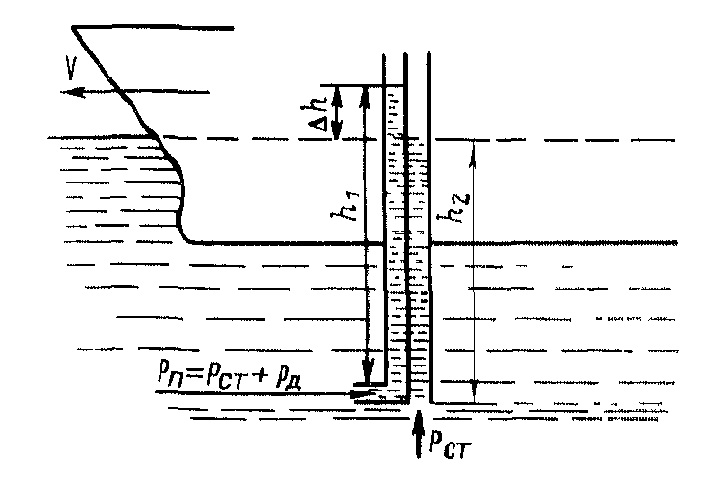 Рисунок 2 – Зависимость гидродинамического коэффициента от скорости судна  В результате измерение скорости с помощью гидродинамического лага сводится к измерению гидродинамического давления, определяемого разностью полного и статического давлений. Пройденное судном расстояние находят, как и в других лагах, интегрированием значений скорости. Приведенные выше формулы справедливы для идеальной жидкости, под которой понимают однородную, неразрывную, несжимаемую и не обладающую вязкостью жидкость. Морская вода таковой не является. Кроме того эти формулы не учитывают гидродинамических характеристик судна, на котором установлен лаг. Учитывают все эти факторы с помощью гидродинамического коэффициента: Pд = kρV2/(2g) (1.6) Коэффициент k определяется эмпирическим путем при натурных испытаниях лага. Возможный вид зависимости k от скорости судна приведен на рисунке 2. Эту зависимость обычно аппроксимируют прямой линией, не проходящей через начало координат: k = a + bV (1.7) где a – постоянный член; bV – переменный член, зависящий от скорости судна (b = tgβ). Следовательно, в гидродинамическом лаге должны быть предусмотрены специальные регуляторы и корректоры для компенсации постоянного и переменного членов уравнения и устранения погрешностей аппроксимации Δ. Рассмотренный выше принцип работы лага позволяет измерить только продольную составляющую вектора относительной скорости судна. [1, стр. 136 – 138] Решение. Выведем формулу для нахождения гидродинамического коэффициента из формулы (1.6): k = Pд/(ρV2/(2g)) Динамическое давление найдем по формуле (1.4): Рд = Рп – Рст Pд = 39 – 20 = 19 [кПа] Зная, что ρ = γ/g, упростим формулу: Подставляя исходные данные в системе СИ, получим: k = 19000кг*м-1*с-1/1025кг/м3*38,044224м2/с2/2*9,8м/с2 = 0,099 Ответ: Гидродинамический коэффициент равен k = 0,099 Задача 51. В результате построения программы работы корректора индукционного лага ИЭЛ-2М для первого участка проведена прямая, которой соответствуют коэффициенты +(1;2). Аналитически определить какая поправка будет введена в показания лага при помощи корректора при скорости судна 5 узлов. Теоретическое введение. Индукционный лаг имеет погрешность, которая должна быть скомпенсирована поправкой Δv . В общем случае поправка лага является некоторой функцией скорости судна, которую можно представить в виде суммы трех составляющих: Δv = f(v) = a + bv + c(v) (2.1) где a - постоянная составляющая, вводимая при регулировке «Установка нуля рабочего» (Уст. 0-Р); bv - линейная составляющая, вводимая при выполнении масштабирования («Масштаб»); c(v) - нелинейная составляющая, компенсируемая с помощью корректора, данные в который вводятся по результатам испытаний на мерной линии. Постоянная составляющая поправки лага вводится во время регулировки прибора в порту или в море при нулевой скорости и штилевой погоде. После выполнения такой регулировки поправка лага имеет линейную и нелинейную составляющие. Определение и ввод линейной составляющей поправки лага - процедуру, которая называется «Масштабирование» - выполняют по результатам испытания лага на мерной линии. Сущность этой процедуры состоит в следующем: - на мерной линии на полном ходу определяются значения истинной скорости vи и лаговой vл; - лаг переключается в режим «Масштаб», при этом в схему лага поступает некоторое эталонное напряжение; - с индикатора снимается отсчет скорости М1, соответствующий этому эталонному напряжению и полученный при предыдущей регулировке; - рассчитывается отсчет скорости М2, который должен показывать лаг при эталонном напряжении с учетом введенной линейной поправки лага; - значение скорости М2 записывается на матовом стекле, которое расположено на внутренней стороне крышки центрального прибора; - регуляторами центрального прибора добиваются, чтобы лаг в режиме масштаб показывал скорость М2 Значение М2 рассчитывается по следующей формуле: M2 = M1*vи/vл (2.2) Ввод нелинейной поправки при помощи корректора состоит в следующем: После того, как постоянная и линейная составляющие погрешности лага скомпенсированы, в отсчете скорости останется только нелинейная погрешность с (ѵ). Кривую с (ѵ) можно представить в виде ломаной линии, на каждом участке которой существует своя поправка, являющаяся линейной величиной. Следовательно, формирование общей нелинейной поправки (в некотором приближении) может быть эквивалентно введению линейных поправок по участкам «Малый ход», «Средний ход», «Полный ход», что в схеме лага ИЭЛ-2М осуществляется при помощи корректора. Рассмотрим последовательность действий по составлению программы работы корректора (рис. 3). Пусть в результате испытаний лага на мерной линии получены поправки лага на трех скоростях: - на малом ходу Δѵ1 = ѵи1 - ѵл1; - на среднем ходу Δѵ2 = ѵи 2 - ѵл 2; - на полном ходу Δѵ3 = ѵи 3 - ѵл3. Значения поправок Δѵ1, Δѵ2, Δѵ3 характеризуют нелинейную составляющую погрешности с(ѵ) в точках А, В и С (рис. 3). Рисунок 3 – Пример графической части расчета программы работы корректора 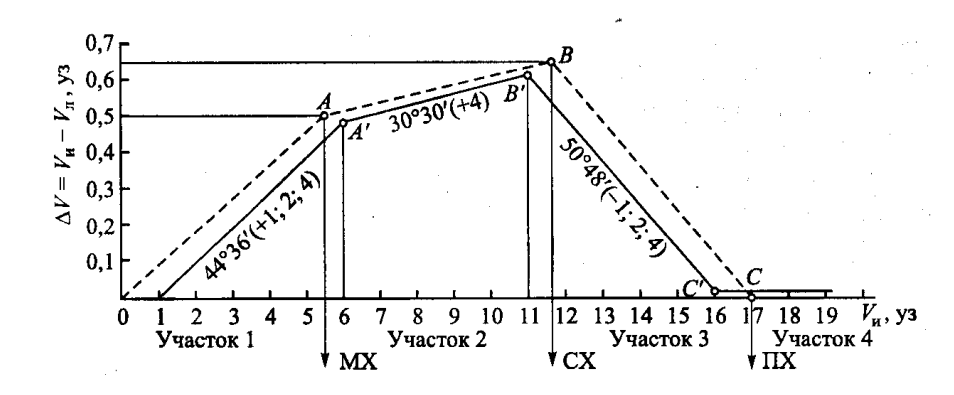 Пользуясь трафаретом, изображенным на рис. 4, на миллиметровку наносят ломаную линию. Эта линия должна состоять из трех четырех участков, при этом каждый участок имеет фиксированный наклон, задаваемый трафаретом. Существует два алгоритма построения фактической АВС и программной А'В'С' ломаных. Первый из них используется, когда скорость полного переднего хода судна составляет 17 узлов и менее. Рисунок 4 – Трафарет для построения программной кривой  В этом случае все точки перегиба ломаной, построенной по трафарету (то есть точки A’, B’ и С’) должны находиться в непосредственной близости от точек А, В и С и соответствовать целому числу узлов. При этом первый отрезок ломаной, построенной по трафарету, должен начинаться со значения 1 уз, а не с нуля. Второй алгоритм предназначен для построения ломаной линии, определяющей программу работу корректора, когда скорость полного переднего хода судна равна более 17 узлов. В этом случае точки A’, B' и С' должны находиться в непосредственной близости от точек А, В и С и соответствовать целому четному числу узлов, а первый отрезок ломаной, построенной по трафарету, должен начинаться со значения 2 уз. Необходимо заметить, что при построении программной ломаной при помощи трафарета важен угол наклона прямых, а, значит, величина используемого масштаба значения не имеет, а значимо постоянство отношений масштабов - то есть в 1 см по оси абсцисс всегда должно быть в десять раз больше узлов, чем по оси ординат. Этому условию, например, удовлетворяют следующий масштаб: по оси ординат (Δѵ) 0,1 уз в 1 см, по оси абсцисс (ѵи) 1 уз в 1 см. Однако выбирать масштаб при построениях необходимо таким образом, чтобы обеспечить наглядность решения задачи и точность нанесения программных прямых на каждом из участков. В итоге каждый из участков будет характеризоваться своей прямой, своим знаком (для прямых, направленных вверх - «плюс», вниз - «минус») и некоторым набором коэффициентов из множества (1; 2; 4). [2, стр. 25 – 30] Решение. Для того чтобы определить какая поправка будет введена в показания лага при помощи корректора при скорости судна 5 узлов построим фактическую А и программную А' прямую при помощи трафарета (рис. 4). Рисунок 5 – Расчет программы работы корректора  Из рисунка видно, что для прямой, которой соответствуют коэффициенты +(1;2) при заданной скорости 5 узлов, соответствует значение поправки Δv = 0,25 уз. Ответ: В показания лага при помощи корректора при скорости судна 5 узлов будет введена поправка Δv = 0,25 уз. Задача 71. На судне, следующим со скоростью 21 узел и сносом 7° , используется четырехлучевой гидроакустический доплеровский лаг с X-образным расположением лучей и частотой излучения 126 кГц. Линия продольных антенн лага смещена относительно диаметральной плоскости судна на угол 43°. Определить направление излучения, если разность частот звуковых волн, принятых продольными антеннами лага равна 1,2 кГц, а поперечными - 770 Гц. Теоретическое введение. Принцип действия гидроакустического доплеровского лага основан на определении скорости судна по доплеровским сдвигам частот акустических сигналов, излученных с борта судна, рассеянных морским дном и принятых антенной системой лага. Рассмотрим работу гидроакустического доплеровского лага. На судне расположены излучатель и приемник акустических колебаний. Излучатель формирует узкий луч, направленный под углом а к горизонту (рис. 4.1). При движении судна длина волны излучения, приходящего к условному приёмнику - морскому дну будет равна: λ1 = λ0 (1 –  cos) (3.1) cos) (3.1)где λ0 - длина волны исходного излучения с - скорость звука в воде, V - скорость судна. Или, переходя к частоте f = с/ λ, можно записать: f 1 =  (3.2) (3.2)Рисунок 6 – Принцип действия гидроакустического доплеровского лага 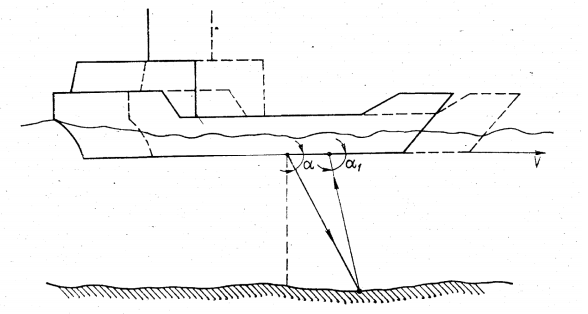 Для высокочастотного излучения, используемого в доплеровских лагах, поверхность морского дна представляет собой совокупность большого числа элементарных отражателей, рассеивающих падающую энергию по всем направлениям, в том числе и к установленному на судне приемнику. За время распространения излучения до грунта и обратно судно сместится (на рис. 6 показано штриховой линией) от положения, в котором происходило излучение сигнала, и прием рассеянного излучения будет производиться под углом 1. Вследствие эффекта Доплера частота принятых на борту судна колебаний отлична от частоты f1:  (3.3) Если предположить, что скорость судна мала и 1, то можно получить следующее выражение для доплеровского сдвига частоты:  (3.4) При использовании электромагнитного излучения, например в радиодоплеровских лагах, во всех практических случаях V << c и членами второго порядка малости в выражении доплеровского сдвига можно пренебречь. В случае же акустического излучения, скорость распространения которого в воде намного меньше скорости света, пренебрегать этими членами уже нельзя. Таким образом, для однолучевой доплеровской гидроакустической системы зависимость доплеровского сдвига частоты от скорости судна нелинейна. Принятый гидроакустическим доплеровским лагом сигнал характеризуется не одной фиксированной частотой, а спектром частот шириной Δfд. Положение этого спектра на оси частот относительной частоты излучения определяется средней доплеровской частотой. Ширина спектра приближенно описывается выражением: Δ |
