курсовая работа по теории автоматов. курс ТА. Теория автоматов
 Скачать 0.88 Mb. Скачать 0.88 Mb.
|
5 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| | Пары состояний, образующих матрицу Т | | Вес перехода P(i, j) | | Суммарный вес перехода | | | Упорядоченная матрица М | |||||||||
| | 1 | 2 | | 1 | | 14 | | | 9 | 1 | |||||||
| | 1 | 3 | | 1 | | 14 | | | 1 | 2 | |||||||
| | 1 | 5 | | 1 | | 13 | | | 1 | 3 | |||||||
| | 1 | 7 | | 1 | | 12 | | | 1 | 5 | |||||||
| | 1 | 8 | | 1 | | 12 | | | 12 | 1 | |||||||
| | 2 | 9 | | 1 | | 10 | | | 1 | 7 | |||||||
| | 3 | 4 | | 2 | | 7 | | | 1 | 8 | |||||||
| | 5 | 6 | | 2 | | 7 | | | 10 | 1 | |||||||
| T= | 6 | 2 | | 1 | | 8 | | M= | 9 | 11 | |||||||
| | 6 | 3 | | 1 | | 8 | | | 6 | 2 | |||||||
| | 7 | 9 | | 1 | | 8 | | | 3 | 4 | |||||||
| | 8 | 9 | | 1 | | 8 | | | 2 | 9 | |||||||
| | 9 | 1 | | 1 | | 16 | | | 6 | 3 | |||||||
| | 9 | 10 | | 1 | | 8 | | | 7 | 9 | |||||||
| | 9 | 11 | | 1 | | 9 | | | 8 | 9 | |||||||
| | 10 | 1 | | 1 | | 12 | | | 9 | 10 | |||||||
| | 11 | 12 | | 2 | | 6 | | | 5 | 6 | |||||||
| | 12 | 1 | | 1 | | 13 | | | 11 | 12 | |||||||
Состояния первой строки матрицы М кодируем начальными кодовыми комбинациями
к(
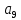 ) = 0000, к(
) = 0000, к(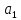 ) = 0001.
) = 0001.Для незакодированного состояния второй строки а2 составляем дополнительную матрицу
 , где ɣ обозначено незакодированное состояние второй строки, равное его номеру. В матрицу
, где ɣ обозначено незакодированное состояние второй строки, равное его номеру. В матрицу  введём все строчки, содержащие ɣ.
введём все строчки, содержащие ɣ.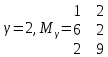 . Множество уже закодированных состояний, содержащихся в матрице M6, равно
. Множество уже закодированных состояний, содержащихся в матрице M6, равно 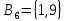 .
. Составляем множество кодовых комбинаций для состояния
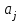 (a6) с учётом условий соседнего кодирования. Для подбора кодов можно использовать карту Карно. Составим карту Карно для трёх переменных и запишем закодированные состояния a9 и a1 в соответствии с их кодами в клетки карты Карно.
(a6) с учётом условий соседнего кодирования. Для подбора кодов можно использовать карту Карно. Составим карту Карно для трёх переменных и запишем закодированные состояния a9 и a1 в соответствии с их кодами в клетки карты Карно.х1 х2
| х3x4  | 00 | 01 | 11 | 10 |
| 00 | а9 | * | | * |
| 01 | а1 | * | | * |
| 11 | * | | | |
| 10 | * | | | |
Так как в переходе а6 – а2 состояние а6 не закодировано, то для нахождения кода для состояния а2 используется только переходы а1 – а2 и а2 – а9. Отметим звёздочками соседние к уже закодированным состояниям а9и а1 клетки карты Карно, получим: для к(а9) = 0000 и к(а9) = 0001 – множество соседних клеток (кодов)
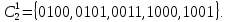
Для каждой кодовой комбинации из
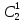 вычисляем
вычисляем 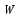 .
.Таблица 3
Расчёт функции W при выборе кода для состояния
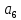
| Соседние коды по карте Карно (множество 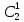 ) ) | Состояние и код | Функция W W = ∑P(i,j)*d(i,j) | |||
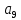 = 0000 = 0000 | 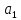 = 0001 = 0001 | ||||
| Вес перехода из 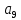 в в 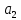 | Кодовое расстояние d(9,2) | Вес перехода из 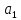 в в 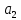 | Кодовое расстояние d(1,2) | ||
| 0100 | 1 | 1 | 1 | 2 | 3 |
| 0101 | 1 | 2 | 1 | 1 | 3 |
| 0011 | 1 | 2 | 1 | 1 | 3 |
| 1000 | 1 | 1 | 1 | 2 | 3 |
| 1001 | 1 | 2 | 1 | 1 | 3 |
Функция Wимеет одинаковое значение для всех кодов, поэтому можно выбрать любой, возьмём по порядку написания код 0100, то есть к(а2) = 0100.
Повторяем пункты 4,5 для того, чтобы закодировать все незакодированные состояния автомата.
Для третьей строки в переходе а1 – а3 не закодировано состояние а3.
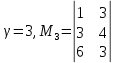 . Множество уже закодированных состояний, содержащихся в матрице М3, равно В3 = {1}.
. Множество уже закодированных состояний, содержащихся в матрице М3, равно В3 = {1}.| х3x4  | 00 | 01 | 11 | 10 |
| 00 | а9 | а2 | | |
| 01 | а1 | * | | * |
| 11 | * | | | |
| 10 | | | | |
х1 х2
Таблица 4
Расчёт функции W при выборе кода для состояния
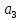
| Соседние коды по карте Карно (множество 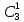 ) ) | Состояние и код | Функция W W = ∑P(i,j)*d(i,j) | ||
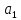 = 0001 = 0001 | ||||
| Вес перехода из 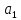 в в 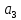 | Кодовое расстояние d(1,3) | |||
| 0101 | 1 | 1 | 1 | |
| 0011 | 1 | 1 | 1 | |
| 1001 | 1 | 1 | 1 | |
Возьмём по порядку написания код 0101, то есть к(а3) =0101.
Для четвёртой строки в переходе а1 – а5 не закодировано состояние а5.
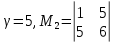 . Множество уже закодированных состояний, содержащихся в матрице M5, равно B5 = {1}.
. Множество уже закодированных состояний, содержащихся в матрице M5, равно B5 = {1}.х1 х2
| х3x4  | 00 | 01 | 11 | 10 |
| 00 | а9 | а2 | | |
| 01 | а1 | а3 | | * |
| 11 | * | | | |
| 10 | | | | |
Таблица 5
Расчёт функции W при выборе кода для состояния
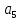
| Соседние коды по карте Карно (множество 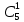 ) ) | Состояние и код | Функция W W = ∑P(i,j)*d(i,j) | ||
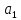 = 0001 = 0001 | ||||
| Вес перехода из 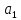 в в 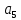 | Кодовое расстояние d(1,5) | |||
| 0011 | 1 | 1 | 1 | |
| 1001 | 1 | 1 | 1 | |
Возьмём по порядку написания код 0101, то есть к(а5) =0011.
Для пятой строки в переходе
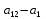 не закодировано состояние а12.
не закодировано состояние а12.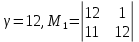 . Множество уже закодированных состояний, содержащихся в матрице M1, равно B1 = {1}.
. Множество уже закодированных состояний, содержащихся в матрице M1, равно B1 = {1}.| х3x4  | 00 | 01 | 11 | 10 |
| 00 | а9 | а2 | | |
| 01 | а1 | а3 | | * |
| 11 | а5 | | | |
| 10 | | | | |
х1 х2
Получим код к(а12) = 1001.
Для шестой строки в переходе а6 – а2 не закодировано состояние а6.
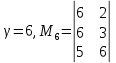 . Множество уже закодированных состояний, содержащихся в матрице M7, равно В7 = {2, 3, 5}.
. Множество уже закодированных состояний, содержащихся в матрице M7, равно В7 = {2, 3, 5}.х1 х2
| х3x4  | 00 | 01 | 11 | 10 |
| 00 | а9 | а2 | * | |
| 01 | а1 | а3 | * | а12 |
| 11 | а5 | * | | * |
| 10 | * | | | |
Таблица 6
Расчёт функции W при выборе кода для состояния
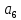
| Соседние коды по карте Карно (множество 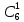 ) ) | Состояние и код | Функция W W = ∑P(i,j)*d(i,j) | ||||
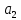 = 0100 = 0100 | 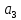 = 0101 = 0101 | |||||
| Вес перехода из 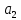 в в 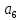 | Кодовое расстояние d(2,6) | Вес перехода из 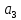 в в 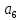 | Кодовое расстояние d(3,6) | |||
| 1100 | 1 | 1 | 1 | 2 | 3 | |
| 1101 | 1 | 2 | 1 | 1 | 3 | |
| 0111 | 1 | 2 | 1 | 1 | 3 | |
| 1011 | 1 | 4 | 1 | 3 | 7 | |
| 0010 | 1 | 2 | 1 | 3 | 5 | |
Возьмём по порядку написания код 1100, то есть к(а6) =1100.
Для седьмой строки в переходе а9 – а11 не закодировано состояние а11.
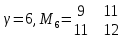 . Множество уже закодированных состояний, содержащихся в матрице M11, равно В11 = {9,12}.
. Множество уже закодированных состояний, содержащихся в матрице M11, равно В11 = {9,12}.| х3x4  | 00 | 01 | 11 | 10 |
| 00 | а9 | а2 | а6 | * |
| 01 | а1 | а3 | * | а12 |
| 11 | а5 | | | * |
| 10 | * | | | |
х1 х2
Таблица 7
Расчёт функции W при выборе кода для состояния
| Соседние коды по карте Карно (множество  ) ) | Состояние и код | Состояние и код | Функция W W = ∑P(i,j)*d(i,j) | ||||
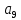 = 011 = 011 | 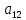 = 100 = 100 | ||||||
| Вес перехода из 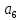 в в 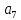 | Кодовое расстояние d(6,7) | Вес перехода из 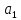 в в 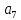 | Кодовое расстояние d(1,7) | | |||
| 1000 | 1 | 1 | 2 | 1 | 3 | ||
| 1101 | 1 | 3 | 2 | 1 | 5 | ||
| 1011 | 1 | 3 | 2 | 1 | 5 | ||
| 0010 | 1 | 1 | 2 | 3 | 7 | ||
Возьмём код к(а11) = 1000.
Для восьмой строки в переходе а7 – а9 не закодировано состояние а11.
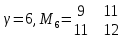 . Множество уже закодированных состояний, содержащихся в матрице M11, равно В11 = {9,12}.
. Множество уже закодированных состояний, содержащихся в матрице M11, равно В11 = {9,12}.| х3x4  | 00 | 01 | 11 | 10 |
| 00 | а9 | а2 | а6 | а11 |
| 01 | а1 | а3 | | а12 |
| 11 | а5 | | | |
| 10 | * | | | |
Получается код к(а7) = 0010.
А
х1 х2
налогично для остальных состояний получаем к(а4) = 1011, к(а8) = 1111,
к(а10) = 1110.
Таким образом, состояния автомата получили следующие коды: к(а1) = 0001, к(а2) = 0100, к(а3) = 0101, к(а4) = 1011, к(а5) = 0011, к(а6) = 1100, к(а7) = 0010,
к(а8) = 1111, к(а9) = 0000, к(а10) = 1110, к(а11) = 1000, к(а12) = 1001.

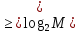 , М – число состояний автомата. Отсюда N =
, М – число состояний автомата. Отсюда N = 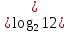 = 4.
= 4. 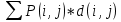 ,
,