тор. Теория электрической связи (37). Теория электрической связи (37)
 Скачать 2.07 Mb. Скачать 2.07 Mb.
|
|
Теория электрической связи (37) 1. Введение 2. Параметры сигнала 3. Искажения и помехи 4. Кодирование и декодирование 5. Модуляция и демодуляция 6. Дискретизация и квантование 7. Достоверность и скорость передачи 8. Классификация радиоэлектронных цепей 9. Параметрические электрические цепи 10. Характеристики нелинейных элементов 11. Графический способ определения отклика НЭ на входное воздействие 12. Аппроксимация ВАХ НЭ 13. Методы определения спектральных составляющих тока через НЭ 14. Метод угла отсечки 15. Метод трех и пяти ординат 16. Умножители частоты 17. Ограничители 18. Модулированные колебания 19. Принципы получения сигнала с AM 20. Практические схемы амплитудных модуляторов 21. Коллекторный модулятор 22. Методы получения однополосных сигналов 23. Сигналы с частотной и фазовой модуляцией 24. Преобразователи частоты 25. Детектирование 26. Синхронное детектирование 27. Детектирование сигнала с ОБП и ДБП при помощи СД 28. Детектирование сигнала с ФМ 29. Детектирование сигнала с ЧМ 30. Квадратурный ЧД 31. Сигнал и помеха как случайный процесс 32. Свойства функции корреляции 33. Разложение сигнала в тригонометрический ряд Фурье 34. Прохождение случайного процесса через НЭЦ 35. Различимость сигналов 36. Оптимальная фильтрация непрерывных сигналов 37. Оптимальный приемник для приема двоичных сигналов 1. Введение Сообщение. Виды сигналов Системы связи предназначены для передачи информации от источника к получателю.  Информация - сведения о каком-либо явлении, событии или состоянии объекта. Получая информацию, мы устраняем ту неопределенность, которая была в нашем сознании. Сообщением (с) называется форма представления информации. Сообщение сигнал Физический процесс одного из параметров, который содержится в передаваемом сообщении, называется сигналом. 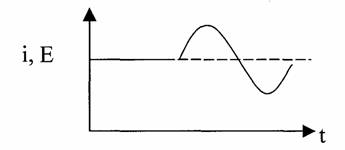 Сообщения из сигнала могут быть непрерывными и дискретными.  Непрерывнымназывается такой сигнал, который принимает любое значение в заданных пределах. Если же сигнал (или сообщение) может принимать любые значения в некотором интервале, то он называется непрерывным по состояниям, или аналоговым. 1) Сигнал, непрерывный по уровню и по времени.  2) Сигнал непрерывный - по уровню и дискретный по времени.  3) Сигнал дискретный по уровню, непрерывный во времени. 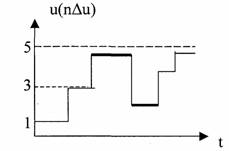 4) Сигнал дискретный по уровню и по времени.  Дискретным по уровню (3) называется такой сигнал, принимает только определенные дискретные значение. Сигнал дискретный по уровню иногда называют квантованным сигналом. Сигнал дискретный по уровню и во времени называется цифровым сигналом (ЦС). Реальный сигнал является функцией времени и носит случайный характер. Все сигналы делятся на: 1. Детермированные сигналы 2. Случайные Детерминированный сигнал - любой сигнал, параметры и мгновенное значение в момент времени могут быть предсказаны с вероятностью единица. Случайные сигналы - функции времени, значение заранее неизвестный могут быть предсказаны лишь с некоторой вероятностью, меньшей единицы.  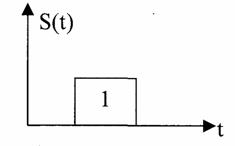  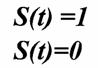 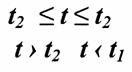 Сигналы известной формы являются испытательными. Детерминированные сигналы представляют собой известную функцию времени (т.е. можно подбирать для них соответствующие математические выражения). Случайным называется такой сигнал, мгновенное значение которого носит случайный характер.  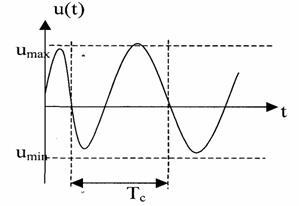 Наиболее полной характеристикой случайных сигналов (процессов) является их n -мерный закон распределения. Чем больше n тем точнее сведения о поведении случайного сигнала (процесса), т.е. n —> ∞ 2. Параметры сигнала 1) Тс - длительность сигнала; 2) Дс - динамический диапазон сигнала Дс = ; g, h =  - отношение сигнала к помехе. - отношение сигнала к помехе.Чем больше g, тем больше вероятность правильного приема.  3) Fc - ширина спектра сигнала, связанных со скоростью изменения сигнала (скорость изменения функции). Большая скорость изменения, следовательно, спектр широкий, меньше скорость изменения - спектр узкий  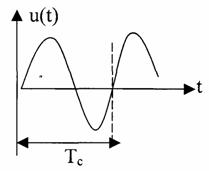   t - время задержки если t увеличивается спектр стягивается. если t уменьшается спектр расширяется, амплитуда уменьшается. Любой сигнал, имеющий форму, отличную от гармонического(cos, sin) является сложным, следовательно, его можно разложить на отдельные составляющие Тc * Дс * Fc=Vc - объем сигнала  При прохождении через КС сигнал искажается. Параметры канала: 1) Тк > Тc (Тк время безотказной работы канала) 2) Дк >Дс (Дк - динамический диапазон канала) 3) fr - ширина полосы пропускания канала. Пропускаются те спектральные составляющие, которые попадают в Fк.  Fк - должно быть таким, чтобы пропускались все спектральные составляющие Дискретным по уровню (3) называется такой сигнал, Тк *Дк * Fк= Vк -объем канала связи. Vк ≥ Vc - достаточное условие для передачи сигнала через КС. Один параметр можно заменить на другой, не изменяя объема. Основные свойства КС: 1) Все КС можно рассмотреть как линейную систему, т.е. к каналу связи применим принцип суперпозиции (то, что подаем на вход, то получаем на выходе). 2) Во всех КС даже при отсутствии полезного сигнала, существует помеха, т.е. канала без помехи не существует.  3) При прохождении через КС сигнал задерживается на некоторое время t и его уровень изменяется m раз. х (t) = m * S (t -t) + W(t) - на выходе. Если m и t не постоянны, то такой канал называется каналом с переменными параметрами. Если на вход приемника сигнал поступает несколькими способами, то такой канал называется многопутевой (многолучевой) канал. 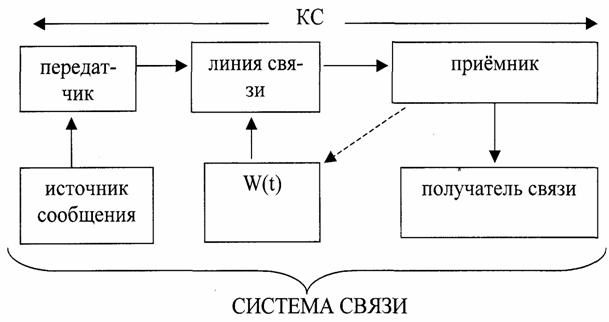 Линия связи - физическая среда, при помощи которой соединяется вход приемника с выходом передачи, или наоборот. Многоканальной - называется такая система связи (СС), которая обеспечивает передачу сообщений от пго количества источников к nму количеству получателей без взаимного влияния.  РУ — разделительное устройство. 3. Искажения и помехи При прохождении через КС сигнал U(t) искажается и U(t) ≠ V(t) Искажения разделяют на два типа: линейные; нелинейные. Линейные искажения (ЛИ) - появляются за счет неравномерности АЧХ и ФЧХ КС или УС. Нелинейные искажения (НИ) - происходят за счет нелинейности АЧХ КС.  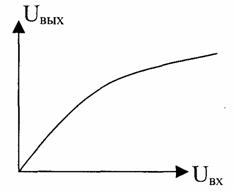   Помехой - называется любое воздействие на полезный сигнал (или приемник), в результате которого ухудшается достоверность принимаемых сигналов. Помехи делятся на внешние и внутренние. К внешним помехам относятся: грозовые разряды, работа сварочного аппарата. электрический транспорт, радиоэлектронная медицинская аппаратура. К Внутренним помехам относятся собственные шумы, шумы элементов устройства. Все эти помехи в зависимости от воздействия на полезный сигнал S(t), U(t) разделяют на две группы: 1. Аддитивная помеха - это помеха которая суммируется с полезным сигналом S(t) + W(t) = X(t) -аддитивная помеха. 2. Мультипликативная помеха X(t) = μ(t) • S(t), где μ(t) - влияние помехи на уровень полезного сигнала. Аддитивная помеха может быть флуктуационной, импульсной(помеха, сосредоточенная во времени), квазигармоническая (помеха, сосредоточенная по частоте). 4. Кодирование и декодирование Кодирование - закон построения сигнала. В результате кодирования дискретные элементы сообщения заменяются совокупностью элементарных сигналов. Обычно в качестве элементарных сигналов используют 0 и 1. Различимые элементы, из которых состоит кодовая комбинация, называется основанием кода. Если основание п больше двух, то это многопозиционный код. Если основание n равно 2, то это двухпозиционный код.  Совокупность элементарных сигналов, соответствующая одному дискретному элементу сообщения, называется кодовой комбинацией. Совокупность кодов комбинаций, соответствующих совокупности дискретных элементов сообщения, называется кодом. Количество элементарных сигналов, из которых состоит кодовая комбинация, характеризует длительность кодовой комбинации и называется значимостью кода. Коды существуют равномерные и неравномерные. Равномерным - называется такой код, кодовая комбинация которого состоит из одинакового количества элементарных сигналов. 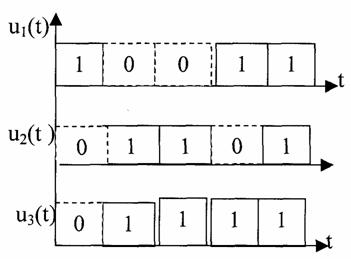 Неравномерным - называется такой код, кодовые комбинации которого состоят из различного количества элементарных сигналов. По помехоустойчивости коды делятся на простые и корректирующие. Простым кодом называется такой код, который не обладает свойством обнаружения и исправления ошибок. В простых кодах все кодовые комбинации закреплены за определенным (дискретным) элементом дискретного сообщения, т.е. свободных неиспользуемых кодовых комбинаций не существует. Корректирующим - называется такой код, который обладает свойством обнаружения и исправления ошибок. Корректирующие свойства появляются за счет введения дополнительных избыточных символов. Можно обнаруживать одиночные ошибки. Для того, чтобы исправлять одиночные ошибки, нужно ввести дополнительный символ. Устройства в которых происходит кодирование, называется кодером. 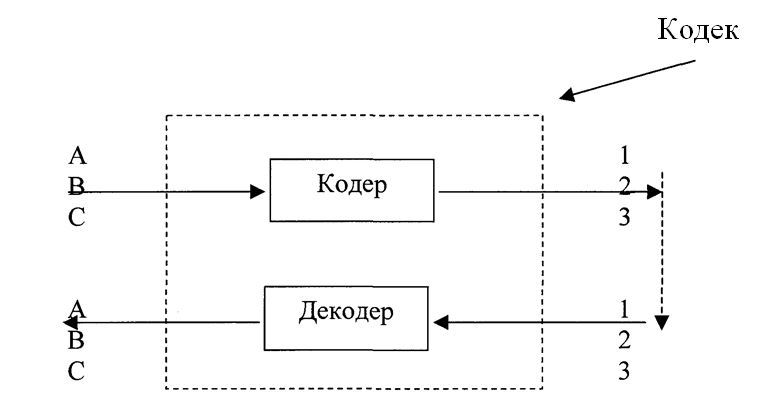 Устройство, в котором происходит обратный процесс, называется декодером. Существует два метода декодирования кодовых комбинаций: 1. Поэлементный прием. 2. Прием в целом. 5. Модуляция и демодуляция В результате модуляции формируется сигнал, передаваемый через канал или линии связи. Так как низкочастотные сигналы не могут передаваться на большие расстояния, то необходимо перейти от низкочастотного сигнала к высокочастотному сигналу. Высокочастотное колебание, в изменении одного из параметров которого содержится передаваемое сообщение, называется несущим (переносчиком). Наиболее часто в качестве несущего используют высокочастотное гармоническое колебание. 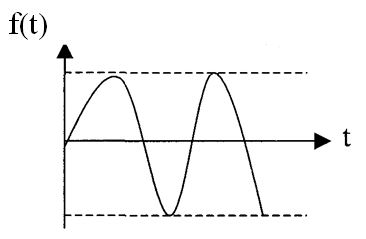   УМ - угловая модуляция, т.к. с изменением фазы изменяется частота. Процесс обратной модуляции называется демодуляцией. 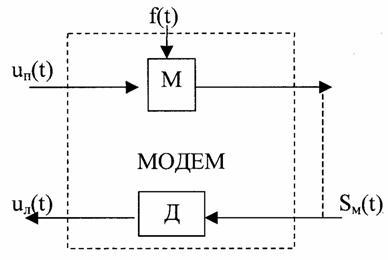 Устройство, в котором происходит демодуляция, называется детектором (Д). Тот параметр несущего, в изменении которого содержится сообщение, называется информационным параметром. В результате детектирования из высокочастотного модулирования выделяется закон информационного параметра. 6. Дискретизация и квантование  Согласно теореме Котельникова любой непрерывный сигнал может быть восстановлен при помощи отсчетных значений, взятых через промежуток времени Δt = l/2Fe. Где 2Fe - верхняя граничная частота сигнала. Дискретизация - замена значений непрерывного сигнала U(t) на отсчетные значения, взятые через промежутки времени Δt = l/2Fe. Дискретизацией по уровню называется - квантованием.  В результате квантования мгновенные значения сигнала заменяются значениями ближайшего допустимого или разрешенного уровня сигнала. Расстояние между ближайшими разрешенными уровнями называется шагом квантования DU. Шаг квантования делится на: равномерный; неравномерный. Цифровой сигнал - сигнал, дискретный во времени и по уровню (сигнал после дискретизации и квантования).  Преимущество дискретизации и квантования - в возможности передавать сигнал дискретным образом. При этом ошибка появляется только в том случае, если уровень помехи превышает шаг квантования. Появляется возможность регенерации сигналов. Другое преимущество - возможность передачи по одному каналу.   Количество каналов определяется длительностью переходных процессов. 7. Достоверность и скорость передачи Характеризуют качество канала (системы) связи и количество сообщений, передаваемых через канал связи (системы связи). Достоверность характеризует качество, а скорость передачи - количество сообщений. Помехоустойчивость - способность системы связи (устройства) противостоять воздействиям помехи. Существуют системы связи, имеющие: 1. Непрерывные сообщения; 2. Дискретные сообщения.  N - общее количество сообщений.  Помехоустойчивость непрерывной системы связи. Любое воздействие на сигнал приводит к уменьшению достоверности. Е2ош= - среднее квадратичное отклонение. Е2ош Е2ош доп Факторы, влияющие на помехоустойчивость: 2. Зависит от формы сигнала, т.е. от способа модуляции степени различимости сигнала. 3. 0т метода приема и дальнейшего способа обработки сигнала. При известном методе модуляции, способе кодирования и уровне помехи, сообщение можно передавать через систему связи с достоверностью (помехоустойчивостью) не выше некоторого предельного. Приемник, который обеспечивает предельную помехоустойчивость, называется идеальным (оптимальным, или приемником Котельникова). Все реальные приемники имеют помехоустойчивость ниже предельной (идеальной). Предельную помехоустойчивость принято называть потенциальной. Скорость передачи - это количество двоичных символов, передаваемых через канал связи за единицу времени (R). R =1/τ0Log2 m , где m - значимость кода При известном виде модуляции, способе кодирования и уровне помехи через систему связи можно пропускать сообщений не более некоторой величины С. С — пропускная способность системы связи — предельное количество сообщений, которое можно пропустить через систему связи. R ≤ С 8. Классификация радиоэлектронных цепей Любая система радиосвязи и средства радиоэлектроники состоят из отдельных функциональных узлов, на вход которого подается x(t); на выходе y(t). 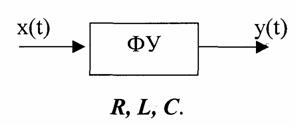 Любой ФУ состоит из резисторов R, конденсаторов С и катушек индуктивности L, соединенных между собой по определенному закону. Транзисторы, полупроводниковые диоды, лампы заменяются эквивалентными схемами с использованием R, L, С.   В зависимости от используемых элементов (элементной базы) различают следующие виды радиоэлектронных цепей: 1. Линейные электрические цепи (ЛЭЦ). а) К ЛЭЦ применим принцип суперпозиции - отклик на суммарное воздействие равно сумме откликов на каждое воздействие в отдельности. б) В ЛЭЦ не происходит обогащение спектра, т.е. не появляются новые спектральные составляющие. 2. Нелинейные электрические цепи (НЭЦ). Если электрическая цепь содержит хотя бы один нелинейный элемент, параметры которого зависят от величины тока I, проходящего через него, и от напряжения U , то такая цепь называется нелинейной. а) К НЭЦ не применим принцип суперпозиции, т.е. отклик на суммарное воздействие не равен сумме отдельных воздействий. б) В НЭЦ происходит обогащение спектра, т.е. появляются новые спектральные составляющие. 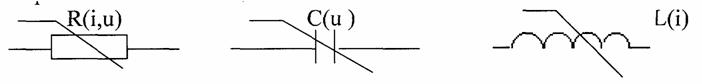 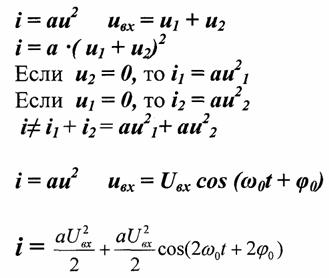 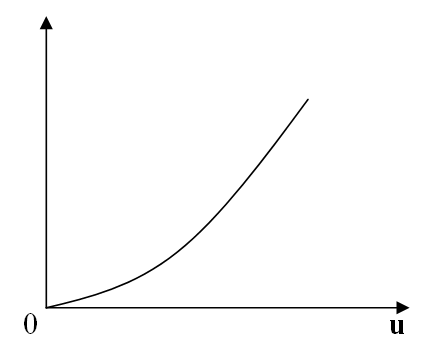 9. Параметрические электрические цепи Если электрическая цепь содержит хотя бы один элемент R(t), L(t), C(t), параметры которого являются функцией от времени, то такая цепь называется параметрической. 1. К ПЭЦ применим принцип суперпозиции. exp = u1 + u2 i = exp g(t)= u1 g(t) + u2 g(t) g(t) = g0 (1 + mgcos t) Mg = g/go - коэффициент изменения проводимости 2. В ПЭЦ происходит обогащение спектра, т.е. появляются новые спектральные составляющие тока. exp (t) = Uex cos ( t+ )  НЕЛИНЕЙНЫЕ ПЭЦ 1. К НПЭЦ неприменим принцип суперпозиции. 2. В НПЭЦ происходит обогащение спектра. 10. Характеристики нелинейных элементов Все элементы R, L, С, при помощи которого определяется эквивалентная схема полупроводникового диода, электронных ламп, могут быть инерционными и безынерционными. 1. Безынерционные. 2. Инерционные.  Характеристики НЭ бывают однозначными и многозначными.   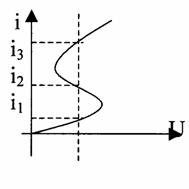 Существуют входные, выходные, переходные характеристики. Входная характеристика iб = Ф (Uбэ) , выходная характеристика iк = Ф(Екэ), переходная характеристика iк = Ф (Uбэ)  Одной из основных характеристик функциональных узлов является его амплитудная характеристика (АХ).  В некоторых случаях является полезным продуктом преобразование несколько или группы спектральных составляющих тока.  Uвх = Uвх cos i1 = I1 cos t Scp = I1/Uвх - средняя крутизна Uвх = I1 Rn ; К = Uвых/ Uвх ; К = Scp Rn ; Scpn = In/Uвх - для п гармоники 11. Графический способ определения отклика НЭ на входное воздействие 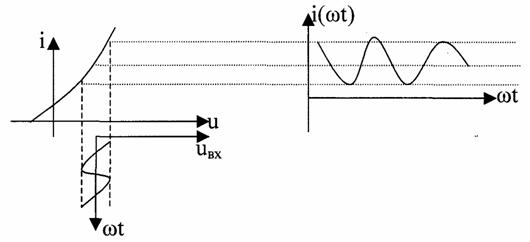  Графический способ определения отклика дает наглядное представление формы сигнала, но не дает возможности определить оптимальный режим работы нелинейного элемента. 12. Аппроксимация ВАХ НЭ Замена реальных ВАХ НЭ, заданных в виде графиков или таблиц, приближенным аналитическим выражениям, называется аппроксимацией. Требования, предъявляемые к аппроксимирующей функции: 1. Аппроксимирующая функция должна быть простой.  2. Аппроксимирующая функция должна быть такой, чтобы в результате анализа можно было выделить нужные спектральные компоненты тока. 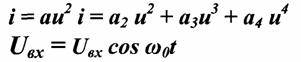 3. Точность аппроксимирующей функции, т.е. насколько точно совпадают значения i и и реальной ВАХ и аппроксимированной. Наиболее часто в качестве аппроксимирующей функции применяют: 1. полином п ой степени: 2. полином 2ой степени: 3. укороченный полином 3ей степени. 4. Укороченный полином 5ой степени. Существует аппроксимация экспонентой i = A∙expau. Аппроксимация суммой экспонент: i = A∙expau+ B expBu+ … 5. Линейно-ломанная аппроксимация (аппроксимация отрезками прямой), если существуют большие уровни входного сигнала. 6. Гиперболический тангенс.
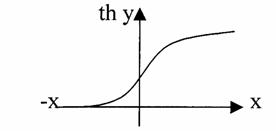 Is - ток насыщения; I0 - ток покоя 7. Аппроксимация функцией Крылова. 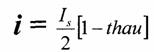 АППРОКСИМАЦИЯ ПОЛИНОМОМ nой СТЕПЕНИ И ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТОВ АППРОКСИМАЦИИ  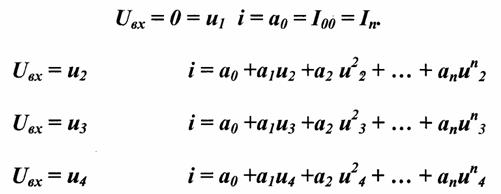 АППРОКСИМАЦИЯ ЭКСПОНЕНТОЙ И ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТОВ АППРОКСИМАЦИИ
Задана ВАХ вакуумного диода  АППРОКСИМАЦИЯ ЛОМАНОЙ ЛИНИИ И ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТОВ АППРОКСИМАЦИИ   Линейная ломаная аппроксимация применяется при больших уровнях входного сигнала. 13. Методы определения спектральных составляющих тока через НЭ  Существуют следующие режимы работы НЭ. 1. Моногармонический режим возбуждения. 2.Биогармонический режим 3. Полигармонический режим Если ( ), можно представить в виде отношения небольших чисел, то такой режим называется синхронным режимом возбуждения. Если ( ), не возможно представить в виде отношения небольших чисел, то такой режим называется - асинхронный. В зависимости от выбора аппроксимирующей функции применяют тот или иной метод определения спектральной составляющей (метод спектрального анализа). 1. Аппроксимация полиномом пой степени. i = а0 +a1u +a2 и2 + ... + anun Используют тригонометрические формулы от кратных аргументов. 2. Аппроксимация ломаной линии: используют метод угла отсечки. 3. Метод трех и пяти ординат, аппроксимация не требуется, спектральные составляющие тока определяются графоаналитическим методом. 4. Аппроксимация экспонентой или сумма экспонент: применяется разложение тока при помощи функции Бесселя от мнимого аргумента. 5. Аппроксимация функцией гиперболического тангенса: разложение в ряд Тейлора. МЕТОД ПРИМЕНЕНИЯ ТРИГОНОМЕТРИЧЕСКИХ ФОРМУЛ ОТ КРАТНОГО АРГУМЕНТА. Этот метод применятся при анализе модуляторов, детекторов, умножителей частоты и т.д. Рассмотрим действие гармонического сигнала на НЭ, ВАХ которого аппроксимирована полиномом 3ей степени.  Спектральные составляющие тока. Спектральные составляющие тока. 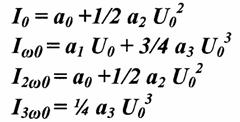 Наивысший номер гармоники равен в степени аппроксимированного полинома. ДЕЙСТВИЕ ДВУХ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ С РАЗЛИЧНЫМИ ЧАСТОТАМИ И НАЧАЛЬНЫМИ ФАЗАМИ  Спектральные составляющие тока.  Комбинационные частоты: Комбинационные частоты:  Комбинационные составляющие характеризуются порядком: 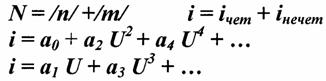 ДЕЙСТВИЕ ДВУХ ГАРМОНИЧЕСКИХ СИГНАЛОВ С КРАТНЫМИ ЧАСТОТАМИ НА НЭ    |