teoria_iggr1 Артур. Теория игр как средство государственного управления
 Скачать 323.65 Kb.
|
|
Заключение Применяя теорию игр в сфере государственного управления можно достичь положительных результатов, которые во многих случаях не могут гарантировать другие науки, однако её использование ограничено определённым кругом критериев, по которым данную ситуацию можно предоставить на рассмотрение с помощью методов теории игр. Наилучшие результаты заметны: в экономической сфере, внешней политике и системе хозяйствования. Овладев базовыми знаниями теории игр, человек сможет применять их в реальной жизни, устанавливать критерии эффективности, позволяющие оценивать преимущество того или иного варианта действий. Это действительно так: зная возможные варианты действий противника или вероятность какой- либо ситуации, можно составить матрицу и решить игру. Положительное результат будет иметь тенденция к внедрению основ теории игр в образовательную школьную программу в качестве дополнительных уроков. Теория игр имеет широкий спектр применения, но она наиболее важна в сфере экономических отношений. Нет сомнения в том, что теория игр может помочь каждому человеку провести математический анализ конкретной ситуации, но достичь карьерного роста, применяя знания теории игр, проще всего экономистам. Однако человеку, чьи знания ограничены, использовать плоды данной науки следует с осторожностью. Список использованных источников: Нейман Дж., Моргенштерн О., Теория игр и экономическое поведение, пер. с англ., М., 1970 Колобашкина Л. В., Основы теории игр: учебное пособие, 2011 Диксит А., Нейлбафф Б., Теория игр. Искусство стратегического мышления в бизнесе и жизни, 2014 Интернет ресурс: https://ru.wikipedia.org/ Приложение 1 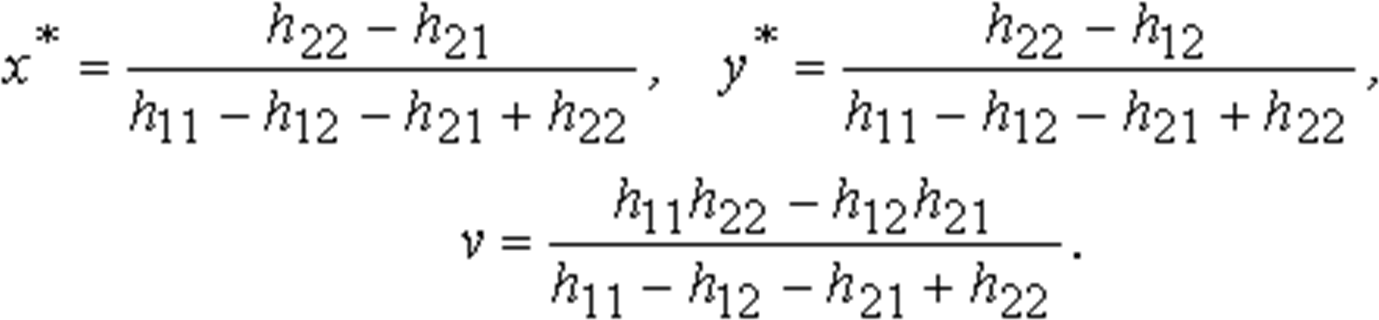 Аналитический метод решения игры 2×2. Формулы:Приложение 2 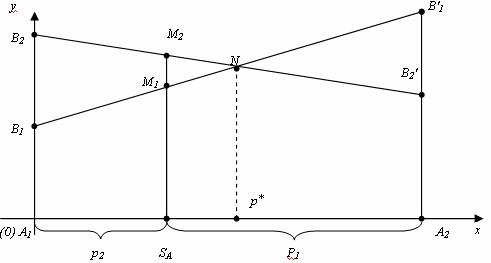 Решение игры в смешанных стратегиях геометрическим методом. Пусть игра задана платежной матрицей . По оси абсцисс отложим единичный отрезок А1 А2, где точка А1(0, 0) изображает стратегию А1, А2(1, 0) – стратегию А2, а каждая промежуточная точка SAэтого отрезка изображает смешанную стратегию первого игрока PA = (p1, p2), где p1– расстояние от точки SA до A2, p2–расстояние от точки SA до A1. Выигрыш игрока Aбудем откладывать на вертикальных отрезках.Случай1. Если игрок B применит стратегию В1, то выигрыш игрока A при стратегии А1равен а11, поэтому на оси ординат отложим отрезок А1В1= а11. При применении игроком A стратегии А2выигрыш равен а21, отложим этот отрезок на перпендикуляре из точки А2, обозначим полученную точку В1'. Ордината любой точки М1отрезка В1В1′равна среднему выигрышу игрока A при применении смешанной стратегии SA. Случай2. Если игрок B применяет стратегию В2, то аналогично откладываем отрезки а12и а22и получаем отрезок В2В2′. Ордината любой точки М2отрезка В2В2′– выигрыш игрока A, если Aприменяет смешанную стратегию SA, а B– стратегию В2. Построим нижнюю границу выигрыша игрока А – ломаную В1 NВ2′. Ординаты точек этой ломаной показывают минимальные выигрыши игрока А при использовании им любой смешанной стратегии. Оптимальное решение игры определяет точка N, в которой выигрыш игрока А принимает наибольшее значение. Ордината точки N равна цене игры. Проекция этой точки на ось ОХпоказывает оптимальную стратегию (р1, р2). Аналогично находится оптимальная стратегия Q = (q1 , q2) игрока B, только в соответствии с принципом минимакса надо находить верхнюю границу выигрыша, т. е. строить ломаную А2NА1′и брать точку N с наименьшей ординатой. Абсцисса точки N определяет оптимальную стратегию игрока B, т. е. Q = (q1 , q2). 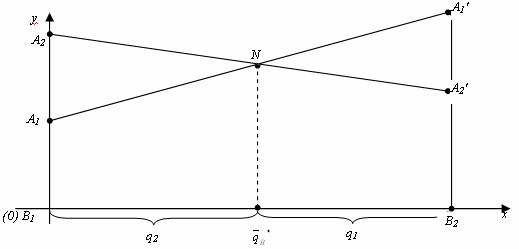 Приложение 3 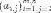 Решение игровых задач в «чистых» стратегиях. Принцип минимакса.        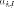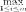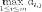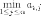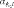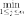Седловой точкой матрицы называют элемент матрицы , удовлетворяющий условиям , то есть элемент матрицы, который одновременно является минимальным элементом в соответствующей строке матрицы и максимальным элементом в соответствующем столбце матрицы, или, что то же самое, элемент матрицы, который одновременно является максимальным элементом в соответствующем столбце матрицы и минимальным элементом в соответствующей строке матрицы. [4] Общее значение нижней и верхней цены игры 𝛼 = 𝛽 = 𝑣 называется чистой ценой игры. Соответствующие седловой точке стратегии Аi, 𝐵j называют оптимальными, они образуют равновесную ситуацию или решение игры. 0 |