Телетрафик курсовик Зарубин. Теория телетрафика методические указания к выполнению курсовой работы
 Скачать 0.67 Mb.
|
|
Министерство связи и массовых коммуникаций РФ ФЕДЕРАЛЬНОЕ АГЕНТСТВО СВЯЗИ Государственное образовательное учреждение высшего профессионального образования «САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕЛЕКОММУНИКАЦИЙ им. проф. М. А. БОНЧ-БРУЕВИЧА»  А.А.Зарубин ТЕОРИЯ ТЕЛЕТРАФИКА МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ КУРСОВОЙ РАБОТЫ Рекомендовано УМО по образованию в области телекоммуникаций в качестве учебного пособия для подготовки бакалавров и магистров техники и технологии и дипломированных специалистов по направлению 210400 "Телекоммуникации" – специальности 210406 "Сети связи и системы коммутации», 210404 "Многоканальные телекоммуникационные системы", 210402 "Средства связи с подвижными объектами», 210407 "Эксплуатация средств связи»  САНКТ-ПЕТЕРБУРГ 2009 Министерство связи и массовых коммуникаций РФ ФЕДЕРАЛЬНОЕ АГЕНТСТВО СВЯЗИ Государственное образовательное учреждение высшего профессионального образования «САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕЛЕКОММУНИКАЦИЙ им. проф. М. А. БОНЧ-БРУЕВИЧА» А.А.Зарубин ТЕОРИЯ ТЕЛЕТРАФИКА МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ КУРСОВОЙ РАБОТЫ Рекомендовано УМО по образованию в области телекоммуникаций в качестве учебного пособия для подготовки бакалавров и магистров техники и технологии и дипломированных специалистов по направлению 210400 "Телекоммуникации" – специальности 210406 "Сети связи и системы коммутации», 210404 "Многоканальные телекоммуникационные системы", 210402 "Средства связи с подвижными объектами», 210407 "Эксплуатация средств связи» САНКТ-ПЕТЕРБУРГ 2009 УДК ББК Рецензент – Рекомендовано к печати редакционно-издательским советом университета Теория телетрафика: методические указания к выполнению курсовой работы / А.А.Зарубин; ГОУВПО СПбГУТ. – СПб, 2009. – 18 с. УДК ББК Рассмотрены теоретические вопросы дисциплины «Теория телетрафика», даны рекомендации к выполнению курсовой работы по данной дисциплине. Предназначены для подготовки бакалавров, магистров техники и технологии и дипломированных специалистов по направлению 210400 – «Телекоммуникации» специальностей 210406 «Сети связи и системы коммутации», 210402 « Средства связи с подвижными объектами», 210407 «Эксплуатация средств связи». © А.А.Зарубин, 2011 © Государственное образовательное учреждение высшего профессионального образования «Санкт-Петербургский государственный университет телекоммуникаций им. проф. М.А.Бонч-Бруевича», 2011 СОДЕРЖАНИЕ
Введение Целью настоящей курсовой работы является получение знаний о принципах функционирования современных центров обслуживания вызовов (ЦОВ) и навыков их проектирования с применением известных математических методов на основании исходных данных, близких к реальным. Основными источниками теоретического материала для выполнения заданий курсовой работы являются курсы лекций «Теория телетрафика ч.2» и «IP-телефония», а также издание СПбГУТ «Методические рекомендации к практическим занятиям. Контакт-центры мультисервисных сетей связи» Б.С. Гольдштейн, А.А. Зарубин, книги «Call-центры и компьютерная телефония» Б.С. Гольдштейн, В.А. Фрейнкман и «IP-телефония» Б.С. Гольдштейн, А.В. Пинчук, А.Л. Суховицкий. 1. Постановка задачи Работа включает разработку обобщенной функциональной схемы ЦОВ на основании заданных архитектурных особенностей, получение искомых характеристик методами аналитического или имитационного моделирования, построение алгоритмов обработки поступающих в ЦОВ вызовов, разработку структурной схемы проектируемого ЦОВ и разработку сценариев взаимодействия ЦОВ с телекоммуникационными сетями общего пользования при обслуживании вызовов. Задание на курсовую работу (п.п. 7) выдается индивидуально и состоит из трех параметров: номер задачи, номер варианта и способ организации коммутационного ядра ЦОВ (коммутатор каналов или система VoIP). Кроме этого, для ЦОВ, построенного по технологии VoIP, должен быть выбран внутренний сигнальный протокол (H.323 или SIP). При взаимодействии ЦОВ с сетью VoIP также определяется сигнальный протокол сети (H.323 или SIP). Пояснительная записка к работе должна быть оформлена на листах формата А4, шрифт Times New Roman, 14, с полуторным интервалом, включать титульный лист, содержание, список сокращений и обозначений, выполненное задание, список литературы. 2. Разработка обобщенной функциональной схемы ЦОВ В соответствии с заданием на курсовую работу необходимо изобразить функциональную схему проектируемого комплекса со всеми внешними интерфейсами и внутренними связями и пояснить назначение каждого приведенного элемента. Функциональная схема должна отражать особенности организации коммутационного ядра ЦОВ и включать набор телекоммуникационных сетей, вызовы от пользователей которых могут обслуживаться данным ЦОВ. 3. Определение характеристик ЦОВ В соответствии с номером и вариантом поставленной задачи определить искомые характеристики проектируемого ЦОВ. Привести указанные диаграммы зависимостей. 4. Разработка алгоритмов обработки вызовов, поступающих на ЦОВ Необходимо привести пошаговый алгоритм процесса обслуживания вызовов, поступающих в заданный ЦОВ с учетом его функциональных особенностей. Предпочтительно представить его в виде диаграммы SDL. Алгоритм должен включать описание действий программно-аппаратного комплекса ЦОВ при приеме/обработке/завершении вызова и действий оператора. Детализация до алгоритма обмена сообщениями на уровне сигнальных протоколов не требуется. 5. Разработка структурной схемы ЦОВ Для выполнения данного раздела курсовой работы требуется привести детальную схему проектируемого ЦОВ в соответствии заданием, которое отражает характеристики, полученные в п.п. 3. Схематично указать пути прохождения поступающих вызовов до рабочих мест операторов (РМО) и обозначить действия всех элементов ЦОВ при этом. 6. Разработка сценариев взаимодействия ЦОВ с сетями общего пользования В соответствии с заданием на курсовую работу и структурной схемой п.п. 5 привести сценарии взаимодействия проектируемого ЦОВ с сетями общего пользования. При этом необходимо учесть, что в случае рассмотрения ЦОВ, построенного на принципах коммутации каналов, РМО и средства компьютерной телефонии центра (IVR и прочие) взаимодействуют с коммутационным ядром по протоколу EDSS-1 (соединения ISDN – BRI и PRI). 7. Задания на курсовую работу (6 задач по 10 вариантов) 7.1 Задача 1. Две группы операторов отдельно обслуживают вызовы, поступающие из ТфОП и VoIP. Пользуясь моделями СМО  для подсистемы ТфОП и  для подсистемы VoIP, определить среднюю задержку запроса на информационные услуги в очередях контакт-центра. Определить число операторов для каждой подсистемы, обеспечивающее среднюю задержку запроса на информационные услуги не более 30 сек.Интенсивность поступления и обслуживания заданы, распределение времени обслуживания вызовов VoIP логнормальное, медленно-затухающее (дисперсия в 2.33 раза больше среднего), см. табл. 1. 7.2 Задача 2. На базе call-центра реализовано предоставление информационных услуг рядом справочных служб. Число служб больше 5, все операторы ЦОВ задействованы во всех службах. Время предоставления информационных услуг распределено по показательному закону и одинаково для всех типов справочных служб. Интервалы времени между поступающими на отдельные службы запросами распределены по показательному закону. Интенсивность поступления задана разная, см. табл. 2. Определить число операторов, обеспечивающее среднюю задержку запроса на информационные услуги в очереди ЦОВ не более 60 сек. и вероятность отказа в обслуживании при этом. Определить среднее число сообщений в общей очереди. Воспользоваться свойствами пуассоновских потоков и моделью СМО .Таблица 1. Варианты задачи 1
7.3 Задача 3. На ступень распределения вызовов (СРВ) поступают три потока вызовов единой экстренной специальной службы (ЕЭСС) – 01, 02, 03. Создается универсальная группа операторов. Очередь вызовов отсутствует. Интенсивность поступления задана разная, вызовы поступают в соответствии с показательным распределением. Время предоставления информационных услуг распределено по показательному закону и одинаково для ЕЭСС, см. табл. 3. Определить число операторов системы, такое, что бы вероятность отказа в обслуживании была не более 0.001. Воспользоваться свойствами пуассоновских потоков и моделью СМО  .Рассмотреть ЦОВ ЕЭСС в соответствии с моделью , определить, при каком числе операторов и длине очереди будет обеспечена вероятность отказа в обслуживании не более 0.001 и время ожидания не более 4 сек.Таблица 2. Варианты задачи 2
Таблица 3. Варианты задачи 3
7.4 Задача 4. Call-центр ТфОП состоит из двух подсистем: операторской и подсистемы IVR (интерактивного речевого взаимодействия). Операторская подсистема реализована как СМО с ожиданием и потерями вида . Подсистема IVR позволяет начать обслуживание речевого вызова сразу же при поступлении его в систему и может моделироваться СМО вида .Для обеих подсистем заданы различающиеся параметры распределений времени обслуживания запросов. Общий входящий поток распределяется на пуассоновские потоки между подсистемами Call-центра в соответствии с указанной пропорцией (операторская/IVR), см. табл. 4. Построить зависимость времени ожидания от числа операторов в системе и определить необходимое число РМО, обеспечивающее время ожидания не более 60 сек. Определить вероятность потерь по вызовам при найденном значении РМО. Определить число каналов, необходимых для подсистемы IVR, которое обеспечивало бы потерю не более 1 вызова из 50. Таблица 4. Варианты задачи 4
7.5 Задача 5. На базе call-центра рядом служб реализовано предоставление информационных услуг. Число служб – 5, операторы ЦОВ разделены на ряд групп, каждой службе сопоставляется своя группа операторов. Время предоставления информационных услуг распределено по показательному закону и различается для всех служб. Интервалы времени между поступающими на отдельные службы запросами распределены по показательному закону. Интенсивность поступления задана разная, см. табл. 5. Определить число операторов для каждой службы, обеспечивающее среднюю задержку запроса на информационные услуги в очереди ЦОВ не более 30 сек. и вероятность отказа в обслуживании. Определить загрузку одного оператора. Воспользоваться моделями СМО .Таблица 5. Варианты задачи 5
7.6 Задача 6. Проектируется контакт-центр, обслуживающий речевые вызовы, поступающие из сети IP-телефонии, сообщения электронной почты пользователей сети Интернет и реализующий подсистему IVR для пользователей сетей IP-телефонии. Время предоставления информационных услуг имеет логнормальное медленно-затухающее распределение и одинаково для обоих типов запросов. Интенсивность поступления запросов различается, а случайные интервалы времени между ними имеют показательное распределение, см. табл. 6. Ожидающие обслуживания запросы не занимают канальную емкость, а контакт-центр может моделироваться СМО вида .Определить число операторов контакт-центра, обеспечивающее среднюю задержку запроса на информационные услуги в очереди не более 30 сек. и среднюю длину очереди при этом по формуле Литтла. Определить среднее число вызовов N, находящихся на обслуживании в подсистеме IVR с учетом показательного характера распределений процессов поступления и обслуживания вызовов. Пояснить возможность применения для моделирования подсистемы IVR модели СМО вида  и привести ограничения применения такой модели. Определить вероятность присутствия на обслуживании 2Nвызовов и рассчитать пропускную способность канала подсистемы IVR необходимую для обслуживания такого числа вызовов N и 2N.Таблица 6. Варианты задачи 6
ПРИЛОЖЕНИЕ. Математические модели систем предоставления информационных услуг В зависимости от характеристик предоставления информационных услуг оборудование ЦОВ может быть представлено в виде различных моделей систем массового обслуживания (СМО), в том числе:
В такой системе вызовы поступают по входящим соединительным линиям от ТфОП и обрабатываются операторами, число которых, как правило, меньше числа линий. Если входящий вызов застает все линии занятыми, то он отклоняется: абоненту телефонной сети будет передан сигнал «занято». Если свободные линии есть, то вызов поступает в систему, а далее, в зависимости от числа свободных операторов, вызов может быть немедленно передан на обслуживание либо поставлен на ожидание. Часть вызовов может уйти из очереди, не дождавшись обслуживания. Для всех неуспешных (не окончившихся обслуживанием) вызовов возможны повторные попытки. Обслуженные вызовы могут уйти из системы или возвратиться в нее для дальнейшего обслуживания. Экспериментально доказано, что распределение интервалов между вызовами для Call-центров ТфОП хорошо соответствует показательному. 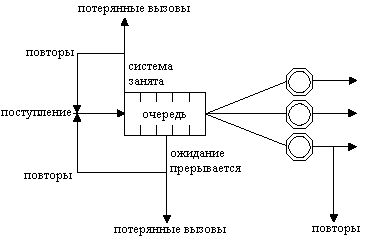 Рис. 1. Функциональная модель Call-центра. МОДЕЛЬ 1. Наиболее простым способом моделирования Call-центра является применение модели СМО типа  с v рабочими местами операторов и неограниченным числом мест для ожидания. Подобная модель не принимает в расчет возможность потери вызовов из-за занятости линий, «настойчивости» пользователя, возможность многоэтапного обслуживания и т.п.. Она является приемлемым средством оценки характеристик множества простых центров обслуживания вызовов. Рассмотрим модель со следующими характеристиками.Интенсивность поступления вызовов:  , n=0,1,2,…;Интенсивность обслуживания  Диаграмма интенсивности переходов для СМО такого типа представлена на следующем рисунке. 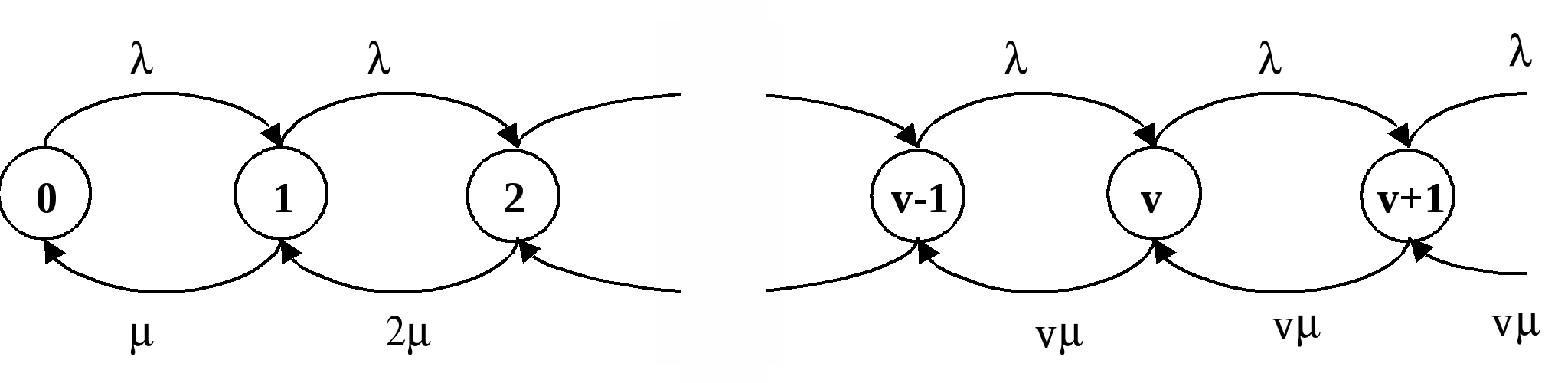 Рис. 2. Диаграмма интенсивности переходов СМО вида M/M/v Рассматриваемая система хорошо изучена, для неё известны следующие результаты. Если принять за  интенсивность поступления вызовов на временном интервале t, а за  среднюю интенсивность обслуживания вызовов на данном интервале, то при  ,  , где  - поступающая нагрузка, а  - коэффициент использования системы. Для системы 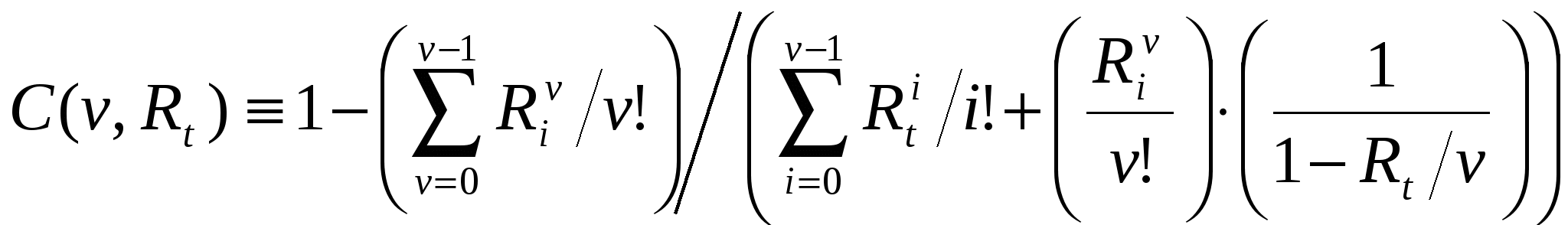известно выражение  , которое также называется С-формулой Эрланга:  (1.1)Среднее время ожидания обслуживания в такой системы вычисляется как  , (1.2)а доля пользователей, время ожидания для которых составит менее Т:  (1.3)МОДЕЛЬ 2. В ряде случаев, при исследовании центров обслуживания вызовов, можно столкнуться с не показательным временем обслуживания заявок. Несмотря на неудобство применения модели СМО вида  известно следующее приблизительное соотношение: , (2.1) где W - среднее время ожидания  - коэффициент вариации, дисперсия  , b – среднее время обслуживания. В случае большой нагрузки на систему  это выражение принимает вид: . (2.2)Данное выражение может применяться для поверхностной оценки искомых значений, когда получение точных результатов аналитически затруднено. МОДЕЛЬ 3. Учесть возможность блокировки вызова по причине отсутствия свободных линий можно при помощи использования модели СМО вида  , для которой известна B-формула Эрланга, которая описывает долю времени, когда все обслуживающие приборы системы заняты.Диаграмма интенсивности переходов для такой системы выглядит следующим образом:  Рис. 3. Диаграмма интенсивности переходов СМО вида .А вероятность занятости всех обслуживающих приборов для такой системы:  . (3.1) МОДЕЛЬ 4. Близкими к оборудованию реальных Call-центров являются модели СМО с ограниченным буферным накопителем. Рассмотрим, модель СМО M/M/v/K. Отметим, что модель M/M/v/K близка по своим свойствам к рассмотренной выше M/M/v, за исключением ограниченного числа мест для ожидания, при переполнении которого поступающие заявки начинают теряться. Предполагается, что 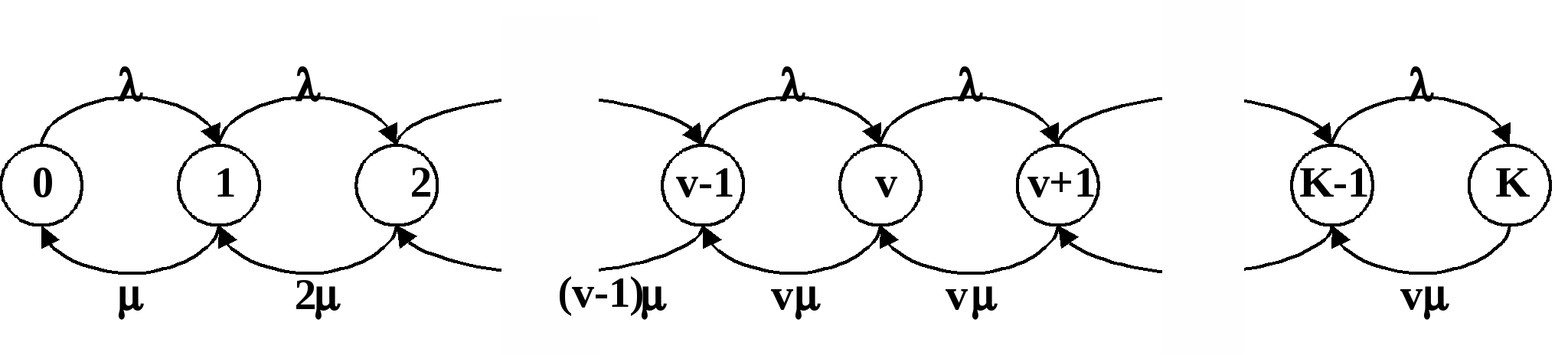 , т.к. в противном случае некоторые обслуживающие приборы никогда бы не занимались, и система функционировала бы как M/M/v/v. На следующем рисунке приведена диаграмма интенсивности переходов для модели СМО M/M/v/K.  Рис. 4. Диаграмма интенсивности переходов СМО вида M/M/v/K. Для описываемой системы интенсивность поступления заявок: 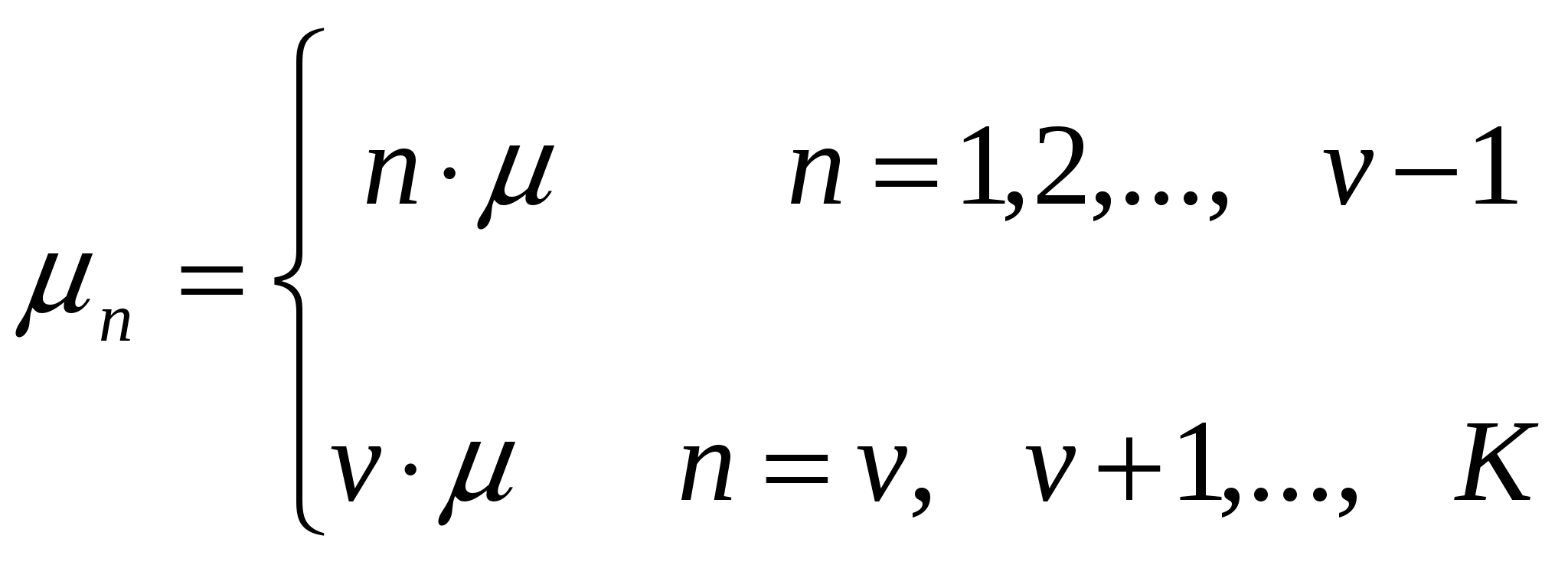  , интенсивность обслуживания:  Известно соотношение, определяющее вероятность заданного числа заявок в системе – n: 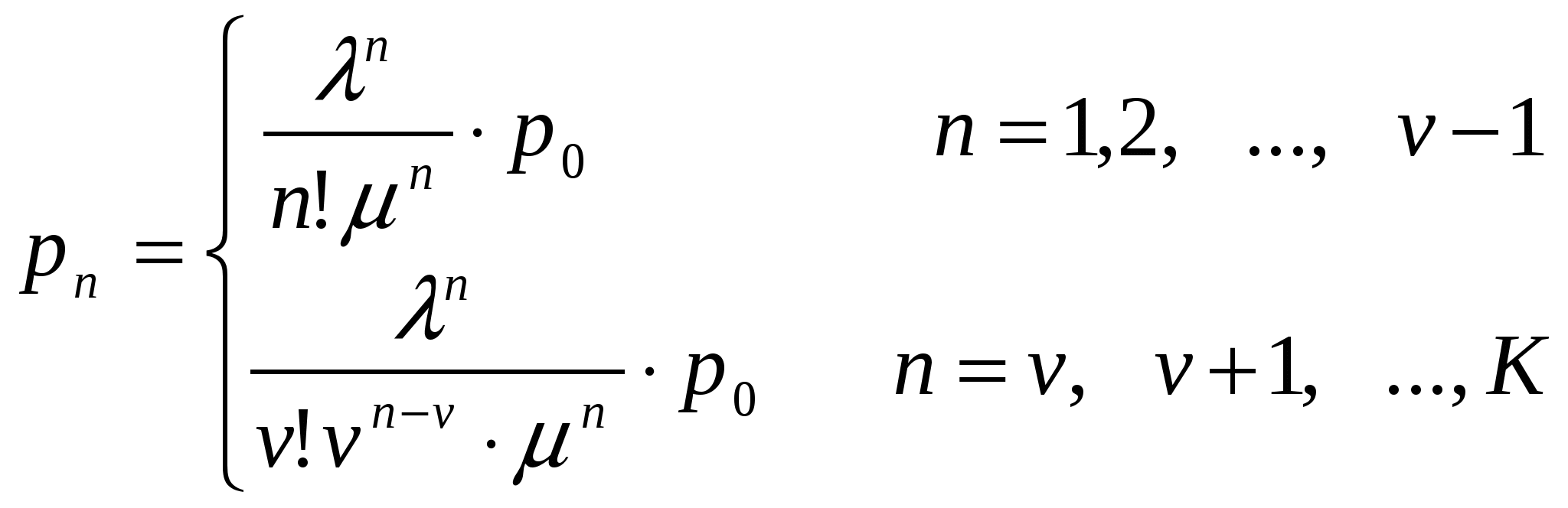 Определяя 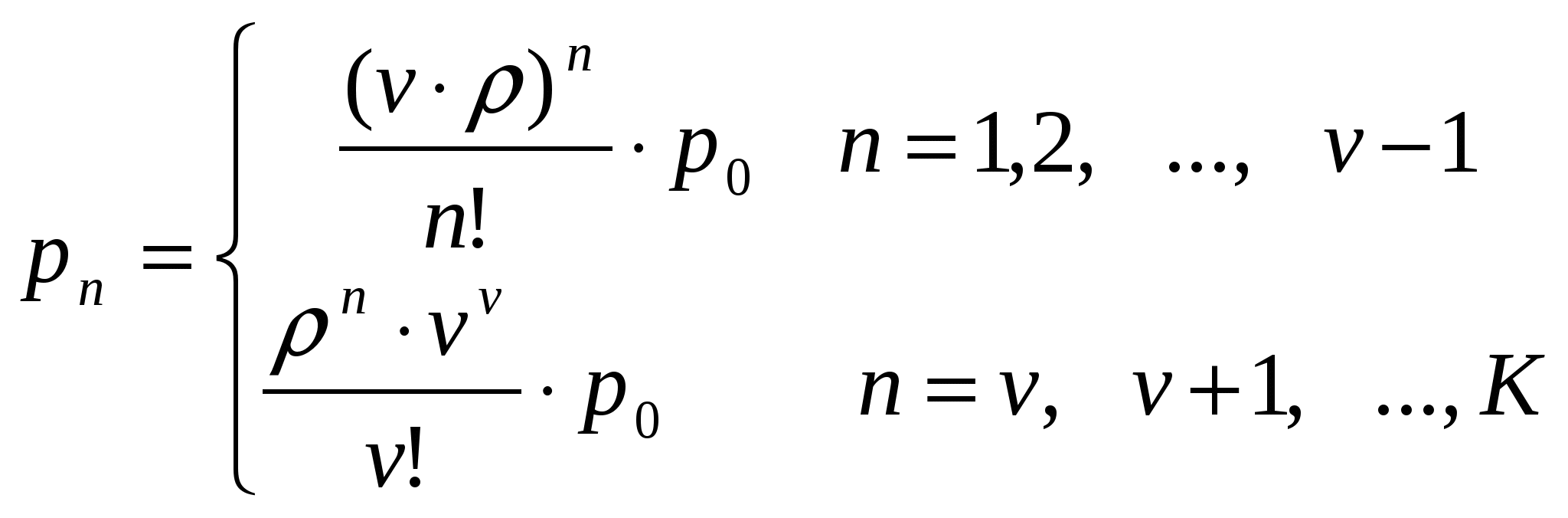 , получаем: Используя известное равенство  можно найти  .Среднее число вызовов в очереди и среднее число вызовов в системе определяется следующими выражениями:   Известно, что все вызовы, поступающие на систему, когда она находится в состоянии n = K, теряются. Т.о. действительная (эффективная) интенсивность поступления заявок в систему вычисляется как  ,где  - вероятность нахождения системы в состоянии K.Разность  определяет интенсивность потерянных вызовов.В данной модели заявки не могут быть потеряны после поступления в очередь. Воспользуемся формулой Литтла для определения среднего времени ожидания обслуживания:  . (4.1) Для модели  с неограниченной очередью загрузка системы определяется по формуле  . В случае ограниченного размера очереди она будет равна:  .А.А.Зарубин ТЕОРИЯ ТЕЛЕТРАФИКА МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ КУРСОВОЙ РАБОТЫ Редактор Л.А. Медведева План 2011 г., п. Подписано к печати Объем 2 печ. л. Тир. 120 экз. Зак. ______________________________________________________________РИО СПбГУТ. 191186 СПб, наб. р. Мойки, 61 Отпечатано в СПбГУТ |
, 
.
с исследованием их поведения при вводе различных систем приоритетов для голосовых и текстовых сообщений.