|
|
Теория вероятности (подготовка к егэ)
Теория вероятности (подготовка к ЕГЭ)
1. Агрофирма закупает куриные яйца в двух домашних хозяйствах. 40% яиц из первого хозяйства — яйца высшей категории, а из второго хозяйства — 20% яиц высшей категории. Всего высшую категорию получает 35% яиц. Найдите вероятность того, что яйцо, купленное у этой агрофирмы, окажется из первого хозяйства.
|
Ответ: 0,75
2. Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика выпускает 35% этих стекол, вторая – 65%. Первая фабрика выпускает 3% бракованных стекол, а вторая – 5%. Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.
|
Ответ: 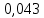 . .
3. В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,3. Вероятность того, что кофе закончится в обоих автоматах, равна 0,12. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.
|
Ответ: 0,52
4. В классе 21 учащийся, среди них два друга — Вадим и Олег. Класс случайным образом разбивают на 3 равные группы. Найдите вероятность того, что Вадим и Олег окажутся в одной группе.
|
Ответ: 0,3
5. Ковбой Джон попадает в муху на стене с вероятностью 0,8, если стреляет из пристрелянного револьвера. Если Джон стреляет из непристрелянного револьвера, то он попадает в муху с вероятностью 0,2. На столе лежит 10 револьверов, из них только 2 пристрелянные. Ковбой Джон видит на стене муху, наудачу хватает первый попавшийся револьвер и стреляет в муху. Найдите вероятность того, что Джон промахнётся.
|
Ответ: 0,68.
6. В случайном эксперименте бросают три игральные кости. Найдите вероятность того, что сумма выпавших очков равна 9. Результат округлите до тысячных.
|
Ответ: 0,116
7. Автоматическая линия изготавливает батарейки. Вероятность того, что готовая батарейка неисправна, равна 0,05. Перед упаковкой каждая батарейка проходит систему контроля. Вероятность того, что система забракует неисправную батарейку, равна 0,96. Вероятность того, что система по ошибке забракует исправную батарейку, равна 0,04. Найдите вероятность того, что случайно выбранная изготовленная батарейка будет забракована системой контроля.
|
Решение:
Вероятность того, что батарейка неисправна, равна 0,05.
Вероятность того, что батарейка исправна, равна 1–0,05=0,95.
Вероятность того, что забракована неисправная батарейка, равна 0,96.
Вероятность того, что забракована исправная батарейка, равна 0,04.
Возможны 2 варианта:
1. батарейка будет исправна и она будет забракована : P1 = 0,95·0,04 = 0,038.
2. батарейка будет неисправной и она будет забракована P2 = 0,05·0,96 = 0,048
Так как может произойти только одно событие, находим сумма вероятностей:
Общая вероятность P = P1+P2 = 0,038+0,048 = 0,086
Ответ: 0,086
8. Если шахматист А. играет белыми фигурами, то он выигрывает у шахматиста Б. с вероятностью 0,5. Если А. играет черными, то А. выигрывает у Б. с вероятностью 0,3. Шахматисты А. и Б. играют две партии, причём во второй партии меняют цвет фигур. Найдите вероятность того, что А. выиграет оба раза.
|
 Решение: Решение:
Возможность выиграть первую и вторую партию не зависят друг от друга. Вероятность произведения независимых событий равна произведению их вероятностей: 0,5 · 0,3 = 0,15.
Ответ: 0,15
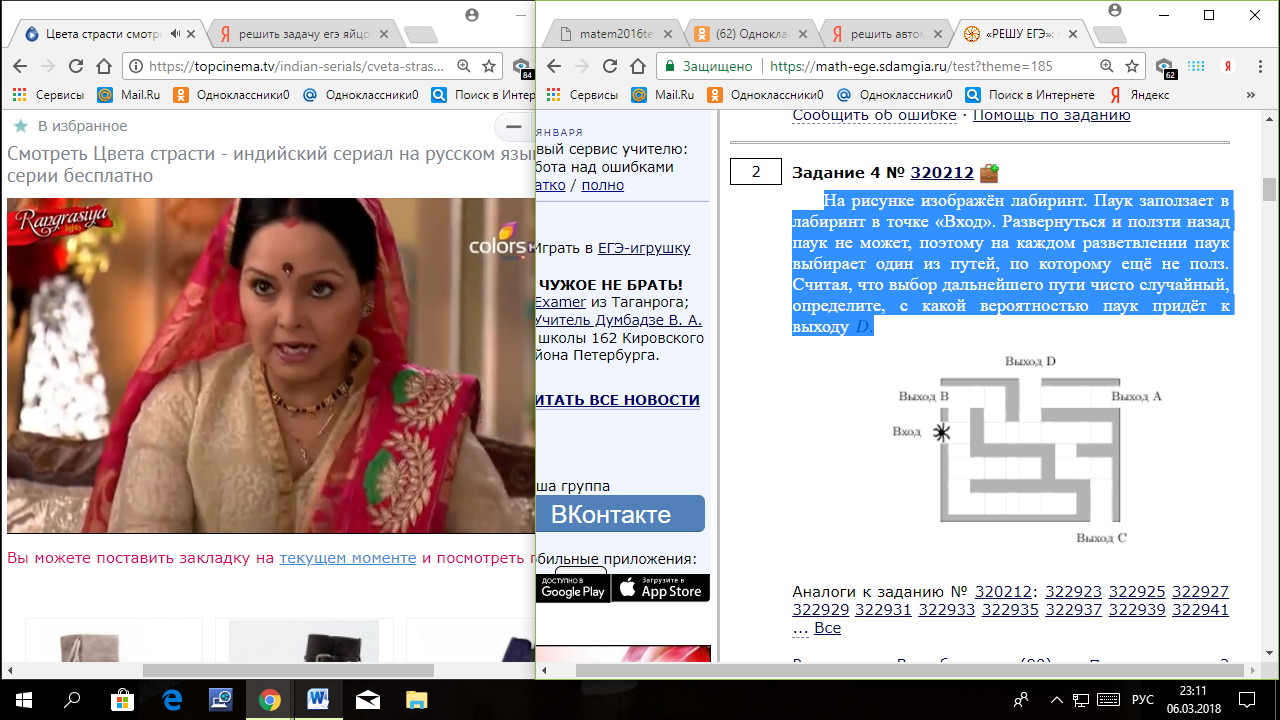
9. На рисунке изображён лабиринт. Паук заползает в лабиринт в точке «Вход». Развернуться и ползти назад паук не может, поэтому на каждом разветвлении паук выбирает один из путей, по которому ещё не полз. Считая, что выбор дальнейшего пути чисто случайный, определите, с какой вероятностью паук придёт к выходу
|
Решение:
Н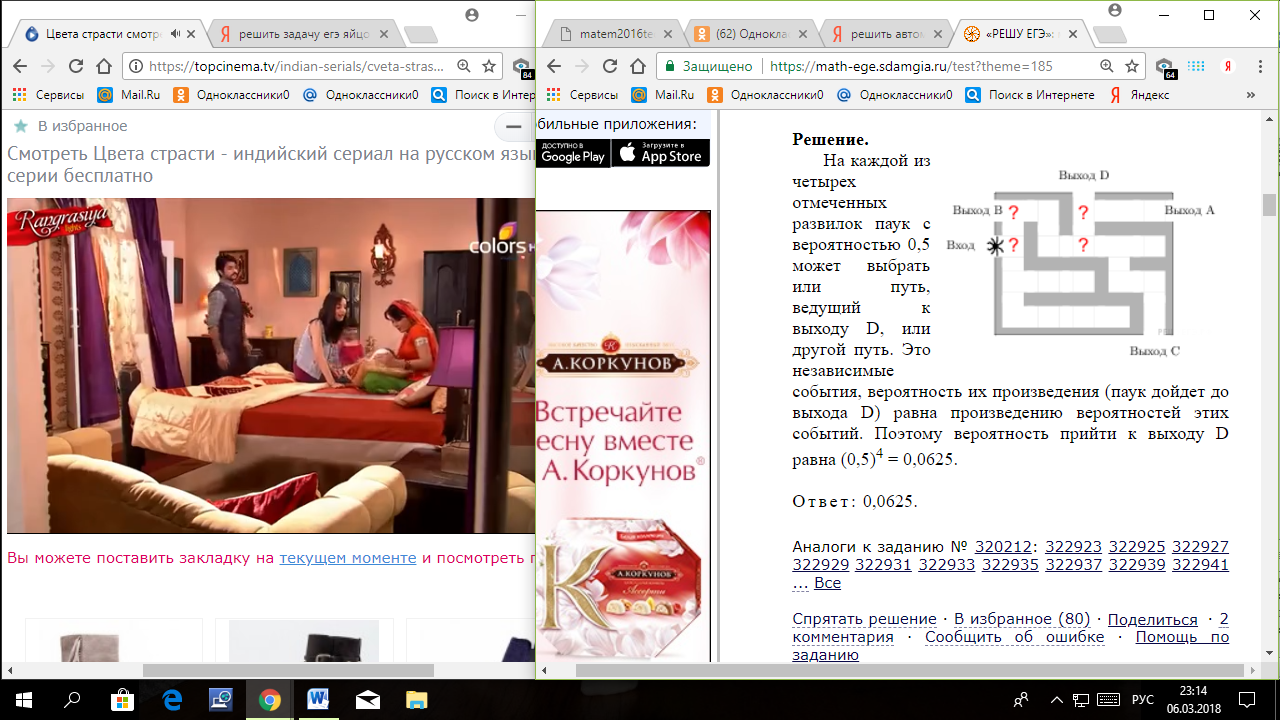 а каждой из четырех отмеченных развилок паук с вероятностью 0,5 может выбрать или путь, ведущий к выходу D, или другой путь. Это независимые события, вероятность их произведения (паук дойдет до выхода D) равна произведению вероятностей этих событий. Поэтому вероятность прийти к выходу D равна (0,5)4 = 0,0625. а каждой из четырех отмеченных развилок паук с вероятностью 0,5 может выбрать или путь, ведущий к выходу D, или другой путь. Это независимые события, вероятность их произведения (паук дойдет до выхода D) равна произведению вероятностей этих событий. Поэтому вероятность прийти к выходу D равна (0,5)4 = 0,0625.
10. Вероятность того, что новый электрический чайник прослужит больше года, равна 0,93. Вероятность того, что он прослужит больше двух лет, равна 0,87. Найдите вероятность того, что он прослужит меньше двух лет, но больше года.
|
Решение:
Пусть A = «чайник прослужит больше года, но меньше двух лет», В = «чайник прослужит больше двух лет», С = «чайник прослужит ровно два года», тогда A + B + С = «чайник прослужит больше года».
События A, В и С несовместные, вероятность их суммы равна сумме вероятностей этих событий. Вероятность события С, состоящего в том, что чайник выйдет из строя ровно через два года — строго в тот же день, час и секунду — равна нулю. Тогда:
P(A + B+ С) = P(A) + P(B)+ P(С)= P(A) + P(B),
откуда, используя данные из условия, получаем
0,93 = P(A) + 0,87.
Тем самым, для искомой вероятности имеем:
P(A) = 0,93 − 0,87 = 0,06.
Ответ: 0,06
|
|
|
 Скачать 0.97 Mb.
Скачать 0.97 Mb.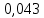 .
. Решение:
Решение: а каждой из четырех отмеченных развилок паук с вероятностью 0,5 может выбрать или путь, ведущий к выходу D, или другой путь. Это независимые события, вероятность их произведения (паук дойдет до выхода D) равна произведению вероятностей этих событий. Поэтому вероятность прийти к выходу D равна (0,5)4 = 0,0625.
а каждой из четырех отмеченных развилок паук с вероятностью 0,5 может выбрать или путь, ведущий к выходу D, или другой путь. Это независимые события, вероятность их произведения (паук дойдет до выхода D) равна произведению вероятностей этих событий. Поэтому вероятность прийти к выходу D равна (0,5)4 = 0,0625. 
